Числовые характеристики (моменты) случайных процессов

При решении ряда задач теории связи нет особой нужды в полной вероятностной характеристике случайных величин, которую дают функция плотности распределения вероятности или интегральная функция. При этом часто приходится также иметь дело с анализом случайных величин, плотности вероятности которых не отражаются аналитическими функциями либо вообще неизвестны. Вместе с тем задание одномерной плотности вероятности р (х_у t_x) позволяет произвести статистическое усреднение и самой величины х_у и любой функции f{x), а также основных числовых характеристик распределений. Под статистическим усреднением (ensemble averaging) подразумевают усреднение по ансамблю реализаций в каком-либо сечении процесса, т. е. в фиксированный момент времени.

Если ср (.г) — известная функция от х (исхода случайного испытания), то по определению ее среднее значение (average value; часто — mean value)

Черта сверху над функцией в формуле (3.3) означает операцию усреднения по множеству результатов случайных испытаний (реализаций). Отметим, что наибольший вклад в среднее значение дают те величины случайного процесса, где одновременно велики как функция ср (лг), так и плотность вероятности р{х).

В статистической теории связи наряду с вероятностными зависимостями F{x) и р{х) для описания свойств случайных процессов используется ряд неслучайных числовых характеристик, называемых моментами распределения {моментами) случайной величины. Моменты распределения случайных величин позволяют оценить случайные процессы уже неслучайными интегральными оценками путем усреднения их по ансамблю реализаций.

Момент /2-го порядка случайной величины X (t) есть среднее значение /2-й степени случайной переменной

Наиболее используемые в статистической теории связи характеристики закона распределения случайного процесса — математическое ожидание (момент первого порядка) и дисперсия (центральный момент второго порядка).

Запишем основные соотношения для вычисления основных числовых характеристик случайных процессов. Во многих практических задачах теории связи требуется вычислять математическое ожидание функции / от случайной величины х, имеющей плотность вероятности р_х{х)_у по обобщенной формуле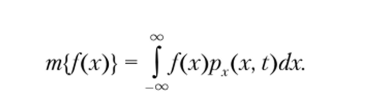

Поскольку принято f (x) = Ху то первый момент, или математическое ожидание {mathematical expectation),

представляет собой среднее значение случайного процесса в текущий момент времени t, полученное усреднением по всему ансамблю. Математическое ожидание (линия т на рис. 3.2, а) служит теоретической оценкой среднего значения случайной величины, получаемой в больших сериях испытаний.

Средний квадрат (второй момент) случайного процесса вычисляют по формуле

При исследовании реальных случайных процессов замечено, что чаще имеют место относительно небольшие отклонения мгновенных значений реализаций от среднего уровня; чем больше отклонения по абсолютному значению, тем реже их наблюдают. В этом проявляется некоторая статистическая закономерность случайных процессов. В системах связи имеют место случайные процессы с нулевым математическим ожиданием, когда реализации группируются по обе стороны от оси времени. Такие процессы называют центрированными.

Дисперсия (variance), или второй центральный момент, определяется математическим ожиданием квадрата отклонения случайного процесса от его математического ожидания:

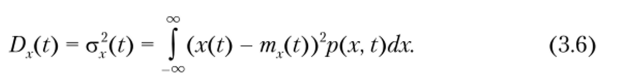
При нулевом математическом ожидании дисперсия характеризует среднюю мощность флуктуаций случайного процесса. Дисперсия случайной величины неотрицательна. Если случайная величина — константа, то D_x(t) = 0. Дисперсию D_x(t) случайной величины часто обозначают через квадрат среднего квадратического отклонения а² = D_x. Удобство использования дисперсии связано с рядом причин. Прежде всего отклонение в большую или меньшую сторону от среднего, равно определяет разброс значений наблюдаемой величины, так что усредняться должны не сами отклонения, а симметричная функция от них. Кроме квадрата можно взять абсолютную величину, четвертую степень, синус и т. п. Выбор квадратичной функции упрощает модель, при этом С КО входит как параметр в закон нормального рас п редел ен ия.

Среди двумерных функций распределения особое место занимает второй смешанный центральный момент — функция корреляции, которая характеризует статистическую связь между значениями одного случайного процесса в два разные момента времени. Функция корреляции позволяет использовать преобразование Фурье и связывать ее со спектральной плотностью мощности случайного процесса.

Функция корреляции.

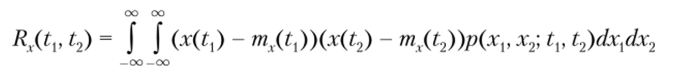
представляет меру связи сечений случайного процесса, взятых в моменты времени t_x и t₂

Когда tj = t₂, т.с. при совмещении сечений случайного процесса, функция корреляции численно равна дисперсии:

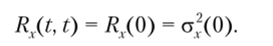
На рис. 3.4 приведены графики некоррелированного (большой разброс значений реализаций) и коррелированного случайных процессов напряжений u (t) = x (t), которые характеризуются практически одинаковыми математическими ожиданиями т.

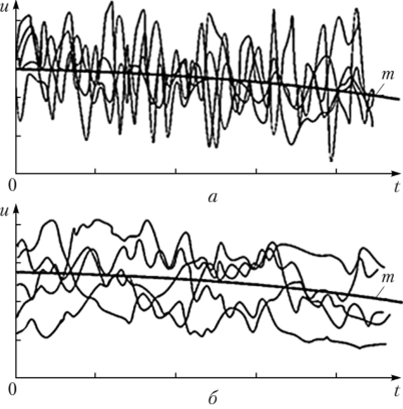
Рис. 3.4. Случайные процессы:

а — некоррелированный; б — коррелированный Из графиков следует, что хотя пространство состояний некоррелированного (рис. 3.4, а) и коррелированного (рис. 3.4, б) процессов практически одно и то же, динамика развития их реализаций различается. Отдельные реализации коррелированного процесса в произвольный момент времени могут быть такими же случайными, как и некоррелированного, а в пределе во всех сечениях оба процесса могут иметь один и тот же закон распределения и одинаковые математические ожидания. Однако динамика развития по координате t единичной реализации коррелированного процесса по сравнению с некоррелированным является более плавной, а следовательно, в коррелированном процессе имеется определенная связь между последовательными значениями случайных величин.

Случайные процессы часто обладают следующим свойством: их функция корреляции стремится к нулю с увеличением временного сдвига т. Чем быстрее убывает функция R (т), тем слабее статистическая связь между мгновенными значениями случайного сигнала в два несовпадающих момента времени.

Наиболее удобной числовой характеристикой быстротечности случайного процесса (скорости изменения реализаций) является интервал корреляции

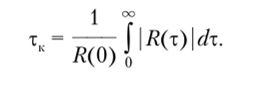
Если известна информация о поведении реализации случайного процесса «в прошлом», то возможен его вероятностный прогноз на интервал ф_к.