Кольцо под действием нормальных и касательных нагрузок

Рассмотрим плоскую задачу о равновесии тонкого кольца, когда к его внешней поверхности приложены усилия.

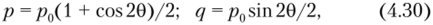
а внутренняя поверхность свободна от нагрузки (рис. 4.3).

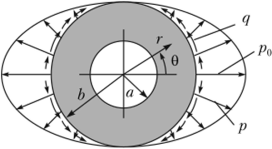
Рис. 4.3. Расчетная схема для кольца под действием нормальных и касательных нагрузок.

Пусть модуль упругости материала кольца изменяется по степенному закону:

а коэффициент Пуассона v = const.

Чтобы удовлетворить граничным условиям задачи.

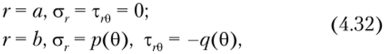
в выражениях (4.23)—(4.25) для напряжений можно ограничиться слагаемыми, содержащими функции <�р₍₎, р, (р_г2 и i_s2:

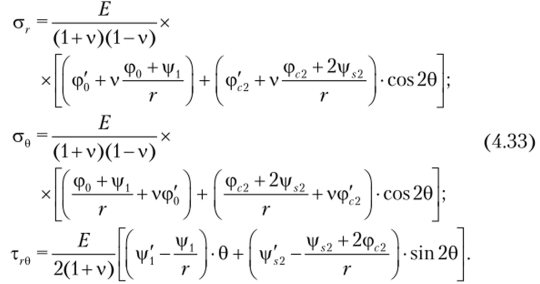
Из системы дифференциальных уравнений (4.7)—(4.22) для определения указанных функций необходимо рассмотреть четыре уравнения (4.7), (4.10), (4.20) и (4.21), которые с учетом равенств е_в = R = © = 0 принимают вид.

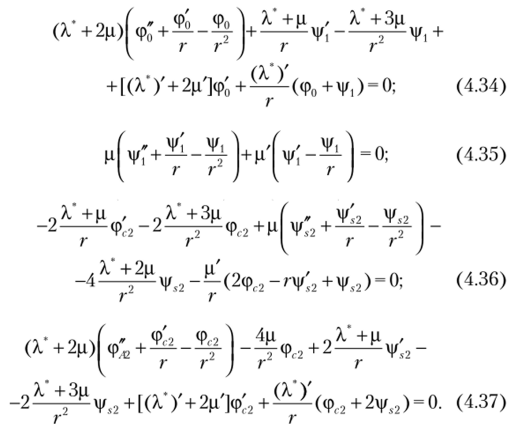
В приведенных уравнениях сделан переход от плоского деформированного состояния, для которого справедливы формулы (4.7)—(4.22), к плоскому напряженному состоянию.

?v.

путем замены параметра X на X = —-у (см. параграф 4.1).

Принимая во внимание, что решение данной задачи с учетом условия однозначности не должно иметь членов, содержащих 0, из третьего равенства (4.33) следует, что.

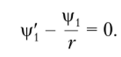
С учетом этого равенства уравнение (4.35) принимает вид.

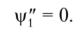
Интегралом данного уравнения является линейная функция, обращающаяся в постоянную величину при.

г = а, b. Учитывая, что граничные условия (4.32) для т,₀ с учетом усилий (4.30) нс содержат постоянной, следует положить у, = 0. Тогда уравнение (4.34) упрощается:

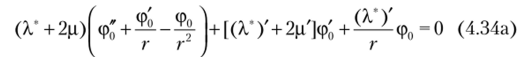
и может служить для определения функции (р₀.

Таким образом, задачу можно разделить на две: определение с помощью уравнения (4.34а) осесимметричной составляющей решения и определение из уравнений (4.36), (4.37) составляющей, зависящей от 0. Подстановка выражения (4.31) в указанные уравнения приводит их к виду.

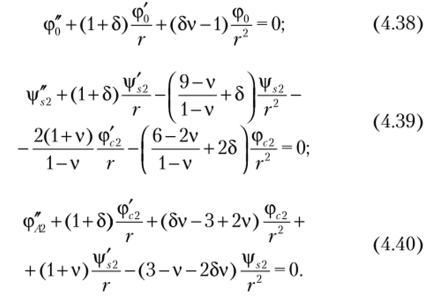
Решением уравнения (4.38) является функция [12].

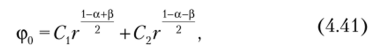
где, а = 1 + 8; р = ^/(1-а)² -4(8v-l).

Константы интегрирования, входящие в решение (4.41), могут быть найдены из граничных условий для осесимметричной составляющей внешней нагрузки:

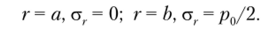
Система двух обыкновенных дифференциальных уравнений (4.39), (4.40) может быть сведена к одному уравнению четвертого порядка следующим образом. Из уравнения.

(4.40) выразим ф'₂ как функцию от ф_х2, а также ф_<2 и ее производных: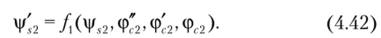

Дифференцируя полученное выражение, но г и подставив в него равенство (4.42), получим.

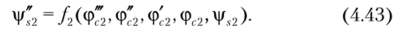
Подставляя равенства (4.42) и (4.43) в уравнение (4.39), найдем выражение для ф_Л.₂:

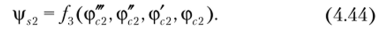
Дифференцируя последнее равенство один раз по г, приравняем полученное выражение соотношению (4.42), подставив в него (4.44). В результате получим уравнение четвертого порядка относительно функции ф_с2:

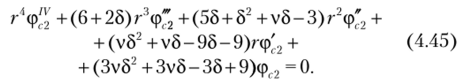
Полученное уравнение можно свести к дифференциальному уравнению с постоянными коэффициентами, введя переменную t с помощью зависимости г = ё:

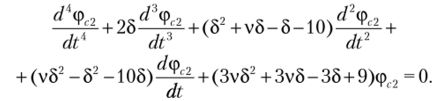
Характеристическим уравнением, соответствующим полученному уравнению, будет.

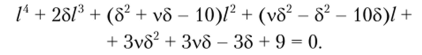
Используя замену ц = I¹ + 5/, данное уравнение можно свести к квадратному:

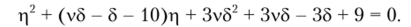
Окончательное решение уравнения (4.45) представляется в виде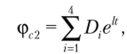

константы которого Z) определяются из граничных условий (4.32) для неосесимметричной составляющей: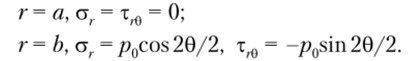

Функцию f_s2 можно найти из равенства (4.44). Приведем пример расчета.

Пример 1. Имеем следующие исходные данные: 5 = -1; b/а = 2; v = 1/3; Е= 2 • 10⁴ МПа. На рис 4.4 показаны эпюры напряжений а₀ вдоль трех направлений радиуса. Из приведенных графиков можно сделать вывод, что учет неоднородности в данном случае не приводит к качественному изменению характера эпюр.

Что же касается численных отличий, то они в некоторых случаях составляют примерно 20%. Естественно предположить, что при более существенной неоднородности отличия в результатах для однородного и неоднородного материала могут быть более выражены.

В данной задаче достаточно просто проследить зависимости перемещений от неоднородности материала. На рис. 4.5 показаны эпюры перемещений точек внутреннего контура кольца вдоль угловой координаты. Можно заметить, что перемещения в неоднородном кольце больше, чем в однородном. Этот факт объясняется тем, что при 5 = -1 модуль упругости уменьшается от внутреннего контура к внешнему в два раза, и это приводит к уменьшению жесткости кольца в целом.

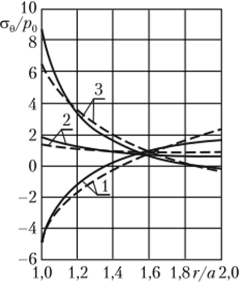
Рис. 4.4. Напряжения а_е в кольце:

1−0 = 0, 2−0 = я/4,3 — 0 = я/2; сплошная линия — неоднородный материал; пунктирная линия — однородный материал.

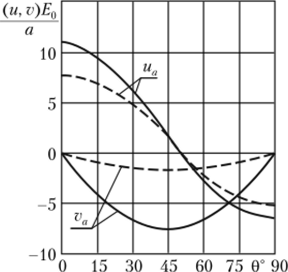
Рис. 4.5. Перемещения точек внутреннего контура кольца:

сплошная линия — неоднородн ы й материал; пунктирная линия — однородный материал В параграфе 4.4 рассмотрен аналитический метод решения обыкновенных дифференциальных уравнений, к которым сводится плоская задача для радиально неоднородного тела. Если вид зависимостей (г), ц (г) и Е (г) достаточно сложный, то получить аналитическое решение не удается. В этом случае необходимо использовать численные методы интегрирования. Метод сведения уравнений в частных производных к системе обыкновенных дифференциальных уравнений с их последующим численным решением называется численно-аналитическим методом (иногда такой метод называют полу аналитическим).

Один из способов численного интегрирования уравнений из системы (4.7)—(4.22) заключается в непосредственной конечно-разностной аппроксимации уравнений второго или четвертого порядка.

Другой способ численной реализации заключается в сведении двух уравнений второго порядка к системе четырех уравнений первого порядка с последующим решением этой системы методом дискретной ортогонализации.

В последующих главах такой метод будет рассмотрен также применительно к трехмерным и двумерным задачам в цилиндрических и сферических координатах.

Достаточно очевидны преимущества численно-аналитического метода по сравнению с любым прямым численным методом (МКР — метод конечных разностей, МКЭ — метод конечных элементов и др.). Для достижения достаточно высокой точности, например в МКР, необходимо использовать густые сетки, что даже в плоской задаче приводит к весьма большим системам алгебраических уравнений. В численноаналитическом методе численная реализация осуществляется на отрезке, и в данном случае практически нет ограничений на количество разбиений данного отрезка.

Нельзя не отметить также некоторые ограничения численно-аналитического метода. Основным является требование одномерной неоднородности материала, т. е. функции неоднородности должны зависеть только от одной координаты. В противном случае не удается осуществить разделение переменных в исходных уравнениях в частных производных. Кроме того, также имеются некоторые ограничения на граничные условия, которые следуют из самой структуры решения. Рассмотрим эти ограничения на примере изучаемой в данной главе плоской задачи в полярных координатах.

Предварительно введем два новых термина. Поскольку существующие методы решения систем обыкновенных дифференциальных уравнений с применением вычислительной техники (метод ортогональной прогонки [8| или метод дискретной ортогонализации) позволяют добиваться практически любой точности, то будем называть квазиточным решение, которое точно удовлетворяет граничным условиям, а приближенность его определяется численным решением дифференциальных уравнений. При этом под словами «точное удовлетворение граничным условиям» понимается либо их тождественное выполнение, либо равенство напряжений соответствующим представлениям внешних нагрузок (например, конечные суммы рядов Фурье). Решение будем называть приближенным, если граничные условия удовлетворяются лишь в отдельных точках границы (метод коллокаций) либо в интегральном смысле.

Рассматривая граничные условия на контуре плоской, в общем случае секториальной области, будем записывать уравнения ее границ в виде 0 = 0, 0₂; г = а, Ь, где 0 < 0, < 0₂ < 2л и 0 < а < b < °о. Если для радиально неоднородного тела поверхностные нагрузки на криволинейных участках контура (г = а, Ь) представлены в виде рядов типа (4.6) (с константами вместо функций, зависящих от радиуса), а на прямолинейных границах (0 = 0, 0₂) выполняются условия, вытекающие из структуры выражений для напряжений и перемещений, то такое решение будет квазиточным. В качестве примера может быть рассмотрена замкнутая кольцевая область, нагруженная системой самоуравновешениых нагрузок, а также любая одномерная задача для кольцевой области. В случае рассмотрения плоского сектора можно получить приближенное решение, если размер сектора вдоль угловой координаты существенно превышает его размер вдоль радиуса (кривой брус).