Ансамбль-вероятность. 
Квантовая физика и неколмогоровские теории вероятностей

Наша интерпретация р-адических чисел.

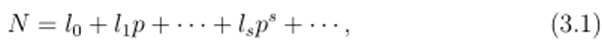
где l_s = 0.1. …, р — 1, с бесконечным числом ненулевых цифр п_$ как бесконечно больших чисел даёт возможность рассматривать многочисленные актуальные бесконечности. Поэтому мы можем изучать ансамбльвероятности на ансамблях бесконечного объёма или рассмотреть классические вероятности для бесконечного числа равновозможных исходов.

• 1. Ансамбли бесконечных объёмов. Мы будем изучать некоторые ансамбли S = 5дг, которые имеют р-адический ‘объём' N. где N
• 5Конечно, мы понимали, что теория Мартин-Лёфа не даёт плодотворного понятия случайности для индивидуальной последовательности испытаний.

р-адическос целое число (3.1). Если N конечно, тогда S — обыкновенный конечный ансамбль, если N бесконечно, тогда S имеет существенно р-адическую структуру. Рассмотрим последовательность ансамблей Mj, обладающих объёмами 1ур>, j = 0,1,… Положим.

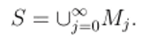
Тогда S = N. Это расщепление ансамбля S будет играть важную роль в наших вероятностных рассуждениях. Следовательно S не просто произвольный ансамбль мощности N, а ансамбль мощности N, построенный с помощью иерархической структуры, соответствующей этому расщеплению. Можно вообразить себе ансамбль S как население живущее в башне Т = Т$, которая имеет бесконечное число этажей со следующим распределением населения, но этажам: население j-го этажа состоит из Mj обитателей. Положим Т* = Это и есть население первых A-f-1.

этажей.

Пусть А С S и пусть существует:

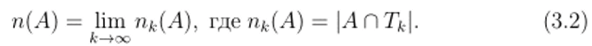
Величина п (А) — это р-адический объём множества А.

Определим вероятность А обычной пропорциональной зависимостью:

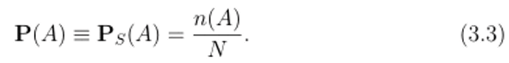
Обозначим семейство всех тех А с 5, для которых предел (3.2) существует, через Qs- Множества A G Qs называют событиями. Позднее мы изучим некоторые свойства семейства событий. Сначала мы рассмотрим алгебру множеств F, которая состоит из всех конечных подмножеств и их дополнений.

Предложение 3.1. Имеет место включение F С Qs- Доказательство. Пусть А конечное множество. Тогда п (А) = А и отношение (3.3) имеет вид:

Теперь пусть В = А. Тогда В П Т^. = |Т*| — А П 7*|. Следовательно существует предел Нт^-де |В П Д. | = N — А. Из этого равенства следует обыкновенная формула:

В частности, имеем: Р (5) = 1.

Предложение 3.2. Пусть Л_ь Л₂ € Gs и Л] Г) Л₂ = 0. Тогда Лi UЛ ₂ Е.

и верно равенство

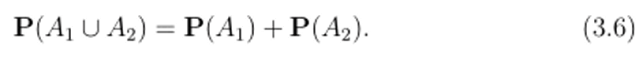
Предложение 3.3. Пусть Л_1? Л₂ Е ?$. Следующие условия эквивалентны: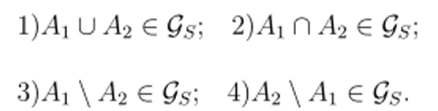

Справедливы стандартные формулы:

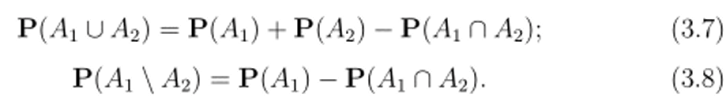
Доказательство. Имеем 7?7_>.(Л₁иЛ₂) = гсДЛ^+пДЛг) — пДЛ^ЛД. Значит, если, к примеру, Л! П Л₂ Е fo, тогда существует предел правой части равенства. Из чего следует AiUA? Е Gs и справедливость формулы (3.7). Другие импликации доказываются аналогично. ?

Следствие 3.1 Семейство Gs является полуалгеброй.

В общем случае из того, что Л_ь Л₂ Е Gs нс следует, что А U Л₂ Е Gs- Чтобы показать это, согласно предложению 3.3, достаточно найти множества Ль Л₂ Е ?/.sтакие, что Л1ПЛ₂ ^ fc. Это легко сделать: пусть множества Ль Л₂ е такие, что |Лi П Л₂ П А//| = 1 для непустого множества Л// (существует только один элемент х Е А П Л₂ на каждом непустом этаже). Если N бесконечно, тогда предел Ниц—юо /ц (Лi П Л₂) нс существует. Значит, семейство Gs ее является алгеброй лсн.ожеста.

Она замкнута только относительно конечных объединений непересекающихся множеств. Однако, Gs не замкнута относительно счётных объединений таких множеств: в общем случае из того, что {А₃ Е Gs, j = 1,2,…, Ai П Aj = 0, i Ф j,) не следует включение U^ijAj Е Gs- Естественные дополнительные предположения (А) ряд Р (А₃) сходится в Q_p или (более сильное предположение), (В) ряд |Р (ЛД|_;> < ос, также нс дают включения Л е Gs;

Пример 3.1. Пусть т = 2, N = -1 = 1 + 2 + 2² 4- • • • + 2″ Н——.

Предположим, что множества А₃ обладают следующей структурой: | Л_; П Л/_ЗЦ—i,| = 1, Aj n M_v-i I = 2^3j-‘ -1иЛ, П A/,' = 0, * + 30 — 1), 3j — 1, т. е. каждое множество A_} размещается на двух этажах башни Т. В частности, Ai П Aj = 0, г ф j. Так как верно включение Aj Е F, то справедливо включение Aj € Gs а вероятность вычисляется по формулам P (i4j) = —2= 1,2…. The series |P (Aj)|2 < oo. Покажем, что A = JjL_xAj g Qs. Имеем:

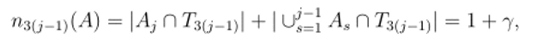
где |7|₂ < 1. Следовательно |пщ-х)(А)₂ = 1. Ho |n_{3 -_i (i4)|2 < 1.}

Отметим следующую полезную формулу для вычисления вероятностей: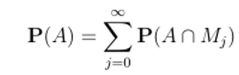

(вероятность найти в башне Т обитателя X со свойством А равняется сумме вероятностей нахождения обитателя с этим свойством на фиксированном этаже).

Определение 3.1. СистемаТ = (S, Gs, Ps) называется р-адическим ансамбль-вероятностным пространством для ансамбля S.

Если N является бесконечным натуральным числом, тогда мы получим ансамбль-вероятностное пространство, которое рассматривалось в главе 1 (при Gs = F$). Фактически, любое ансамбль-вероятностное пространство V может быть приближено ансамбль-вероятностными пространствами Vu, обладающими конечными объёмами. Положим.

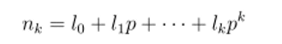
для N. которое имеет разложение (3.1). Пусть l_s — первая ненулевая цифра в разложении (3.1). Рассмотрим конечные ансамбли S_nk,

|S_nJ = щ (k = s, s+l,…), и ансамбль-вероятностные пространства ‘Рп. = {Sn_k, Gs_nk, Ps-_rlfc). Множество Gs_nk совпадает с алгеброй Fs_nk всех подмножеств конечного ансамбля S,_lk, а определение ансамбль-вероятности (3.3) совпадает с определением данным в главе 1:

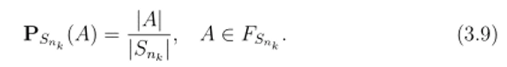
Мы отождествляем S_nk с населением первых к —1−1 этажей башни 7 $.

Предложение 3.4. Пусть А Е QsТогда существует предел

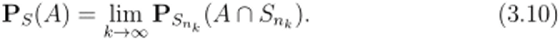
Для доказательства (3.10) мы только воспользовались тем, что множество Q, является топологической группой. Это приближение существенно зависит от правила (способа) измерения, который определяется последовательностью {да}, которая, в свою очередь, и даёт приближение бесконечного ансамбля S конечными ансамблями {5″_fc}. В принципе, изменение этого правила может изменить предельный результат (подробнее об этом см. |60|).

Предложение 3.5. (Образ ансамбль-вероятности). Вероятность Р отображает множество Qs ^{6 ша}Р Ur_s(0), где rs = 1/|ЛГ|_р.

Для того, чтобы исследовать условные вероятности нам следует расширить понятие р-адической ансамбль-вероятности, чтобы рассматривать ансамбли более общего вида.

Пусть S — население башни 7 $ с бесконечным числом этажей Л/, j = 0,1,… и следующим распределением населения по этажам: mj элементов на j-ом этаже, nij Е N, а ряд m.j сходится в Z_p к ненулевому числу N = S. Определим р-адическую ансамбль-вероятность для множества Л С 5 по формулам (3.2), (3.3); Qs будет соответствующим семейством событий. Легко убедиться в том, что для этой более общей вероятности предложения 3.1−3.5 также справедливы.

Пусть А е Qs и Р (Л) ф 0. Мы можем рассматривать множество А в качестве нового ансамбля с р-адической иерархической структурой А = U? L₀Map где Myj = А П Mj, и ввести соответствующее семейс тво событий Qа;

Предложение 3.6. (Условная вероятность) Пусть А € fc, P (i4) ф 0 и В € QаТогда В е Qs и справедлива формула Вайет.

Доказательство. Башня Та ансамбля А имеет следующую структуру населения: по Ма₃ элементов на j-ом этаже. В частности, Т_Ак = 7*ПЛ. Таким образом, справедливо равенство.

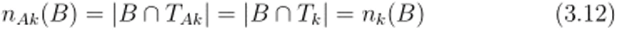
для каждого множества В с А. Значит, существование предела па (В) = Нпц.-юо ПАк (В) влечёт' существование предела п$(В) = 1шц-_>оо Щ-(В). Кроме того, эти пределы равны, а, значит, имеет место равенство:

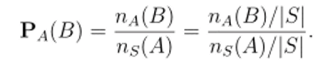
По формуле (3.12) получаем следующее следствие.

Следствие 3.2. Пусть А, В? Qs-P (A) ф 0, и В С А. Тогда верно включение В? Qa;

Следовательно, мы получим формулу.

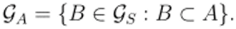
Пусть А, В, АГВ? Qs- Р (-А) ф 0. Положим по определению Р_А(В) = Рл (Л П В). Тогда верна формула.

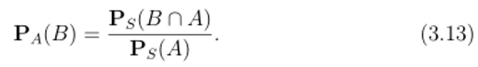
Если мы положим, что Р_А(В) = Р(В/А) и опустим индекс S при вероятностях по ансамблю S, тогда получим формулу Байеса.

Замечание 3.1. Мы много раз обсуждали область применения формулы Байеса. На этот вопрос имеется точный и простой математический ответ в рамках р-адической теории ансамбль-вероятностей. Мы можем использовать формулу Байеса для событий А и В тогда и только тогда, когда пересечение А П В также является событием, т. е., А П В? Qs- Замечание 3.2. Для физических приложений важно, что семейство Qs не является алгеброй множеств, а вероятность P. s может, в принципе, принимать любое значение х? U_rs. Манипуляции, использовавшиеся при доказательстве неравенства Белла (глава 2), неприемлемы для ансамбль-вероятностного пространства V = (5, Qs- Ps). К примеру, если есть три множества Вф, Во, Во € Qs, тогда, в принципе, возможно, что имеют место включения Вф П Во, Вф П Во, Во П Во? Qs, но Вф П Во П Во ф Qs- Кроме того, вероятности могут, в принципе, быть отрицательными. В этом случае мы нс можем воспользоваться стандартной оценкой для колмогоровсих вероятностей.

2. Правила обращения с р-адическими вероятностями. Один из основных инструментов обычной теории вероятностей основывается на структуре порядка в поле вещественных чисел R. Он даёт возможность сравнивать вероятности различных событий; события Е с вероятностями Р(Е) <�С 1 рассматриваются как маловероятные, а события Е с вероятностями Р (?") «1 рассматриваются как практически достоверные. Тем не менее, использование этих соотношений в конкретных приложениях существенно основано на нашей (вещественной) вероятностной интуиции. Что такое большая вероятность? Что такое малая вероятность? Кроме того, не легко сравнить две произвольные вероятности. Например, вы предпочитаете выиграть с вероятностью P (Ei) = или с P (i?2) = ЦФормально, так как Р (?ч) < Р(Е2) было бы лучше выбрать событие Е-2. Но на практике такой выбор не даёт больших преимуществ. Значит, обычная вероятностная интуиция больше основывается на сотнях экспериментов, чем на точной математической теории.

Если мы хочем работать с р-адическими вероятностями нам следует развить некий тип р-адической вероятностной интуиции. Однако, здесь возникает математическая проблема, которая не даёт возможности прямого обобщения вещественной схемы. Эта проблема отсутствие структуры порядка на Q,. Конечно, мы что-то можем делать и без структуры порядка. Например, мы можем расклассифицировать (разделить) различные события с помощью их р-адических вероятностей. К примеру, это работает достаточно успешно в частотной теории вероятностей. Если имеются две последовательности х и у (порождённые некоторым статистическим экспериментом), которые не являются 5-последовательностями в обычной частотной теории фон Мизеса, тогда мы не смогли бы разделить свойства последовательностей х и у. Обе эти последовательности с вещественной точки зрения полностью беспорядочны. Однако, если они являются (5, т_р^последовательностями, тогда было бы возможно расклассифицировать их с помощью р-адических распределений вероятностей, Р_х(а,). Р_?/(о,). В ансамбль-подходе различие р-адических вероятностей, P. s-fE'i) ф PsiE-z), означает, что события Е и Е2 имеют различные р-адические объёмы.

Однако, мы могли бы сделать намного больше с р-адическими вероятностями, используя структуру частичного порядка, который имеется на кольце р-адических целых чисел.

(О) Пусть х = хоХ…х_п… и у = У0У1 …у_п — — канонические разложения двух р-адических целых чисел .т, у € Z_;). Полагаем х < у если существует п такое, что х" < у_п и ад. < уь для всех к > п.

Эта структура частичного порядка, заданного на Z_;, является естественным продолжением структуры стандартного порядка, заданного на множестве натуральных чисел N. Легко видеть, что х < у для любого элемента ж € N и у € Z_p N, т. е., любое конечное натуральное число меньше любого бесконечного числа. Но мы не сможем сравнить любые два бесконечных числа.

Пример 3.2. Пусть р = 2 и пусть х = —1/3 = 10 101…1010…, 2 = —2/3 = 0101…0101… и у = —16 = 0001…1111…. Тогда х < у и z < у, но числа х и z несравнимы.

Важно отметить, что существует максимальное число N_max € Z_;>. Легко видеть, что оно равняется:

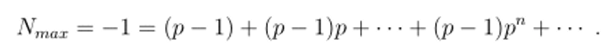
Следовательно, ансамбль 5_i самый большой ансамбль который только может быть рассмотрен в рамках р-адического анализа.

Замечание 3.3. Кажется естественным предположение о том, что объём ансамбля возрастает с возрастанием показателя р, т. е., |5^| < ISithp < <7;

Предложение 3.7. Пусть N € Z_р, N ф 0. Тогда Sn 6 Gs-_х и справедливы равенства: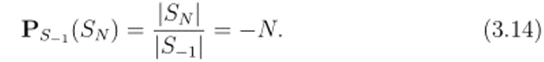

Следствие 3.3. Пусть N € Z_p. N Ф 0. Тогда Qs_N С Gs-i, а вероятности Ps_v(A) вычисляются как условные вероятности относите. аьно подансамбля S, w ансамбля Sпо формуле:

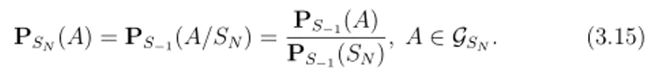
Однако из включения Л € Gs-_X не следует, что А П S, v € Gs_N?

Согласно следствию 3.3, мы можем, фактически, ограничить наши рассмотрения случаем максимального ансамбля S-Таким образом, будем изучать этот случай S = 5_i.

Порядок (частичный) О, заданный на множестве р-адических целых чисел Z_p даёт возможность сравнивать р-адические объёмы п (А) множеств А € Gs- Естественно говорить, что вероятность Р(В) больше чем вероятность Р (Л) если р-адический объём п (В) множества В больше чем р-адический объём п (А) множества А. Следовательно, мы получаем следующее отношение частичного порядка на множестве вероятностей:

(0) Р(В) > Р{Л) тогда и только тогда, когда п (В) > п (А).

Мы используем те же самые символы >, < для обозначения этого нового порядка на Z_;,. Надеемся, что читатель не будет путать эти два порядка, заданных на Ъ_р: 0-порядок используется при сравнении р- адических объёмов, 0-норядок используется для сравнения вероятностей. Например, пусть р = 2 и пусть п (В) = — 2(= 011…1…), п (Л) = —3(= 1011…1…). Тогда п (В) > п (А) (относительно порядка О) и следовательно Р(В) = 2 > Р (Л) = 3 (относительно порядка О)

Изучим некоторые свойства вероятностей.

• (1) Поскольку мы имеем только отношение частичного порядка, мы не можем сравнивать вероятности произвольных двух событий А и В.
• (2) Так как х < — 1 относительно порядка О для любого элемента х € Z, имеем соотношение Р (А) < 1 = Р (.$) для любого события А € Gs-
• (3) Поскольку х > 0 относительно порядка О для любого элемента х € Z_p, имеем неравенство Р (Л) > 0 для любого события А € Gs-

Чтобы проиллюстрировать дальнейшие свойства р-адических вероятностей, воспользуемся третьим отношением порядка, а именно, обычным (как в вещественном случае) отношением порядка на множестве Z_pH Q. В этом случае мы будем говорить о /'-возрастании или г-убывании. Этот г-порядок на Zp П Q не обладает вероятностным смыслом. Мы рассматриваем этот порядок, потому что хотим использовать ‘вещественную интуицию', чтобы представлять расположение рациональных вероятностей Р (Л), А € Gs, на вещественной прямой. Мы будем использовать символы [а, 6],…, (а, Ь) для обозначения соответствующих интервалов вещественной прямой. К примеру, пусть р = 2 и пусть Р(В) = 2, а Р (Л) = 3. Тогда Р (?) > Р (Л), но с точки зрения г-порядка вероятность Р(В) меньше чем Р (Л).

(4) Положим = {А Е Gs • и.(Л) € N}. ⁶

Сужение порядка О на множество натуральных чисел N совпадает с обыкновенным порядком (порядком вещественных чисел) на множестве N. Значит, п (А) < п (В), А, В € F*, тогда и только тогда когда натуральное число п (А) меньше чем натуральное число п (В). Из этого.

⁶ В частности, pf содержит все конечные подмножества множества S. Совокупность F* содержит также некоторые бесконечные подмножества А € Qs, которые обладают конечными р-адическими объёмами. Например, пусть величина А П 7*| = 1 + р^к, к = 1,2,… (1 + р^к обитателей первых (к + 1) этажей обладают свойством А). Тогда п{А) = 1, и, следовательно, имеет место включение А € F*.

следует (по определению порядка О на множестве вероятностей), что Р: F* -* (—оо, 0) П Z, а функция Р (Д) возрастающая если функция Р (Л) г-убывающая. Таким образом, например, вероятности Р (Л) = — 1 или —3 довольно малы в сравнении с вероятностями Р (Б) = —100 или -300.

(5) Положим F* = {В = А: А € F^f} (в частности, совокупность F* содержит дополнения всех конечных подмножеств множества П). Тогда функция Р: F^f —> N и Р (?) убывающая если функция Р (В) — г-возрастающая. Значит, к примеру, вероятности Р (Е) = 100 или 200 довольно малы относительно вероятностей Р© = 1 или 2.

Можно пользоваться этими правилами и для условных вероятностей. Например, пусть Р (В) = 100, Р(В') = 200, Р (А) = 2 и В, В' с А. Тогда справедливо неравенство Р (В/А) = 50 > Р (В'/А) = 100.

По правилам (4) и (5) мы можем работать с вероятностями, принадлежащими совокупности F^f U F.

(6) Теперь рассмотрим события, удовлетворяющие условию А? F* U F*. Мы можем развить свою интуицию только благодаря примерам.

Пример 3.3. Пусть р = 2. Пусть | А П М_2к = 2^2А' и А П M₂k+i = 0, к = 0,1,…. Тогда п (А) = -1/3(= 1010…10…), а Р (Л) = 1/3. Пусть В С А и выполняются условия: В П Мм = А П Мм, В П Mj = 0, j / 4к. Тогда п (В) = —1/15(= 100 010 001…10 001…), а Р(В) = 1/15. Очевидно, что —1/15 < —1/3 в Z₂. Значит, Р(В) = 1/15 < Р (Л) = 1/3.

Отсюда следует, что, но-видимому, вероятностное отношение порядка на множестве [0,1] П Q совпадает с общепринятым вещественным порядком. Кроме того, видимо, оправдано использовать это отношение также и в случае когда числа п (А) и п (В) несравнимы в Z₂^[1].

Пример 3.4. Пусть р и А — такие же как и выше. Пусть ICnA^+il = 2²*⁺¹, СПМ_2к = 0, к = 0,1,…. Тогда п© = -2/3, а Р© = 2/3. Числа п (А) = —1/3 и п© = —2/3 несравнимы в Z₂. Но эвристически кажется очевидным, что можно воспользоваться структурой r-порядка на отрезке [0,1] для сравнения вероятностей событий А и С. Значит, вероятность события uj е С в два раза больше чем вероятность события oj € А. Эти эвристические доводы также подтверждаются некоторыми частотными статистическими моделями, см. работу [60].

Кроме того, мы имеем, что вероятность того, что х? (—ос, 0) П Z практически незначительна, но сравнению с любой вероятностью того, что у? (0.1] П Q. Предлагается следующий интуитивный довод. Вероятность Р (Л)? (—oo.OJflZ является вероятностью события А с конечным р-адическим объёмом в бесконечно большом ансамбле S. Вероятность Р (Л)? (0,1] П Q является вероятностью события А с бесконечным радическим объёмом в бесконечно большом ансамбле S.

Таким образом, р-адика даёт возможность расщепить вероятность 0 на множество вероятностей, 0 —> Dq; в частности, (—сю, 0) П Z С .

Замечание 3.4. Вероятность Р на булевой алгебре А не вырождается: Р(А) = 0, А? А тогда и только тогда, когда А = 0. р-адическое расщепление вероятности 0 может рассматриваться как шаг в направлении к булевым вероятностям. Множество новых меток Ц} даёт возможность расщепить много вероятностей, которые должны равняться вероятности 0 с точки зрения вещественного анализа. Однако, мы ещё не получили булевой вероятности. Имеются многочисленные события А? Qs, Л / 0, вероятность которых 0. Например, пусть А ПТ*! = р^к, к = 1,2,…. Тогда верно равенство Р (Л) = 0.

Можно также использовать эти правила для условных вероятностей. К примеру, пусть Р(В) = 1/15 < Р (В') = 2/15, Р (Л) = 1/5 и В. В' С А. Тогда верно неравенство Р{В/А) = 1/3 < Р (В'/А) = 2/3. Кроме того, например, пусть Р(В) = — 1 < Р{В) = —5, Р (Л) = —100 и В, В' С А. Тогда неравенство Р{В/А) = 1/100 < Р (В'/А) = 1/20 справедливо. Значит, структура г-порядка на (0,1] П Q воспроизводит правило (4).

Предложение 3.8. Если верно включение Р (В)? N, тогда сщтведливо включение. п (В)? {0} U N; если Р{В)? (0,1) П Q, тогда п (В)? Z_PN.

Доказательство. Если k = Р (?)? N, то п (В) = —к, к = 1,2,…, и п (В) = -1 + к. Если, а = Р (?)? (0,1) П Q тогда п (В) = -а и п (В) = а- 1? N. _ ?

Таким образом, если Р(В) € N, тогда множество В имеет конечный р-адический объём, п (В). С другой стороны, если Р (В)? (0, l) flQ. тогда множество В имеет бесконечный р-адический объём, п (В). Естественно предположить, что вероятность Р(В)? N больше любой вероятности Р(С)? (0,1) DQ.

Следовательно, р-адика даёт возможность расщепить вероятность 1 на множество вероятностей, 1 . В частности, N С Df. Однако, вероятность 1 расщеплена ещё не полностью. Имеются многочисленные события А Ф 0 с вероятностью Р (Л) = 1. Например, пусть | А П Л4| =.

p ((fc+i)/2] _ij_:_ 1,2,… (здесь [x] обозначает целую часть числа х). Тогда п (А) = -1 и Р (Д) = 1. Но А ф<�А.

Можно также расщепить все вероятности х — Р (А)? (0,1) П Q.

Пусть А е Gs, x = Р (А)? (0,1) П Q. С? F^f, АПС = 0, и пусть В = A U С. Тогда верно равенство Л = Р (В) = Р (Л) + Р© = х — к, где Р(С) = —к, к? N. Так как р-адический объём множества С конечен (а ансамбль S бесконечен), вероятность Р(С) = —к бесконечно мала. Следовательно, вероятность х может расщепиться на множество вероятностей D± Каждая вероятность Л? D* больше чем вероятность х, а вероятность А = — х = —к бесконечно малая.

Пусть выполнены условия: В? Qs, С? F*, В П С = 0, и пусть А = В U С, х = Р (Л) € (0,1) П Q. Тогда справедливы равенства Л = Р (В) = Р (А) — Р© = х + к, где величина Р© = —к, к? N, является бесконечно малой вероятностью. Значит, вероятность х может расщепиться на множество вероятностей D~. Каждая вероятность Л? D~ меньше чем вероятность х, а вероятность А = х — А = — к является бесконечно малой.

Таким образом, вероятность х расщепляется на множество вероятностей D_x = D~ U D+.

Теперь рассмотрим вероятности относительно ансамбля 5дг для произвольного числа N? Z_P, N ф 0. Используя формулу (3.15), можно свести рассуждения к результатам общего вида, полученным для ансамбля S = S-1. В общем случае вероятность 0 расщепляется на множество Dq, которое содержит в себе множество {А = 77: &? N}; вероятность 1 расщепляется на множество, которое содержит множество (А = 1 — 77: к? N}; вероятность х? (0,1) П Q расщепляется на множество D_x = D~ U DJ, где D~, в частности, содержит множество {А = х —: к? N}, a множество D+ содержит множество.

{А = гг +^: /г? N}.

3. Отрицательные вероятности и р-адические ансамбль-вероятности. Давайте рассмотрим пример 2.2 главы 1 с р-ад и ческой точки зрения. Ряд S = 1+2+…+2* + … = —1 сходится в Q>. Значит, статистический ансамбль S из примера 2.2 имеет 2-адичный максимальный объём -1. Вероятности р* = |5(А = Л^)|/|>9| = — 2^к являются бесконечно малыми вероятностями. Из р-адичсского подхода следует, что распределение квантовых систем относительно значений, А = Aj скрытых переменных обладает 2-адичной иерархической структурой. Ансамбль S имеет вид башни, в которой j-ый этаж ‘населяется' квантовыми системами $ со свойством Л = Aj. Если мы предположим, что подготовительная процедура ? производит порции квантовых систем в соответствии с этой структурой башни, то возникнет весьма нестабильное поведение свойств, А = A j в квантовых данных, которые будут использоваться в эксперименте (ср. с |67|).

Суммирование в формуле полной вероятности.

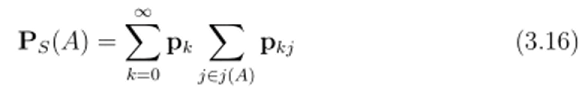
имеет смысл с точки зрения Q₂ для условных вероятностей р/,_;, которые не зависят от к (для конечных множеств А).

Теперь рассмотрим пример 2.3 главы 3. Здесь условные вероятности ры = — 2^/ корректно определены в Q₂. Они являются бесконечно малыми вероятностями. Суммирование в формуле (3.1G) имеет смысл. Например, для А = {AJ,'_2к,…} имеем:

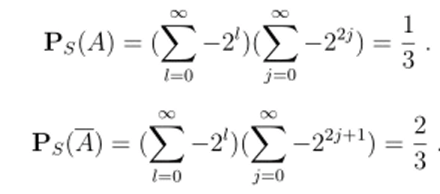
Все вышеупомянутые ряды сходятся в пространстве Q_L>.

Наконец, рассмотрим пример 2.4 из главы 3. Согласно равенству (1.10) ряд, составленный из факториалов &!, сходится в любом поле Q_/(. Следовательно, условные вероятности.

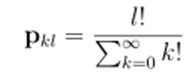
корректно определены в каждом поле Q_/(.

• [1] Однако, вероятно, это неверная экстраполяция, и мы должны предполагать существование событий с несравнимыми вероятностями.