Модели с неизвестным лагом и сущность авторегрессионного преобразования

Последовательное увеличение числа лагов, включаемых в модель (164), как мы только что констатировали, неэффективно ни с вычислительной, ни с содержательной точки зрения. Поэтому на практике изначально предполагают бесконечное число лагов и стараются либо найти критерий их ограничения, либо модифицировать исходную модель таким образом, чтобы избежать подбора величины лага.

Так, в методе, предложенном Койком, предполагается, что коэффициенты при лаговых значениях объясняющей переменной убывают в геометрической прогрессии. Таким образом, задается связь.

в которой выполняется неравенство 0 < А < 1, что отражает скорость убывания коэффициентов с увеличением лага. Данное предположение достаточно логично, если считать, что влияние прошлых значений объясняющих переменных на текущее значение зависимой переменной со временем угасает.

Представление (168) позволяет исходную модель (164) преобразовать в уравнение.

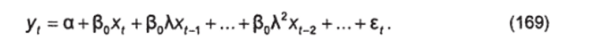
Параметры данного уравнения а, Р₀ можно определить, например, путем присвоения параметру Л значений из интервала (0; 1) с произвольным фиксированным шагом (0,01; 0,001 или 0,0001). Для каждого из значений, А рассчитывается величина.

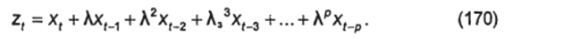
Значение лага р определяется из условия, что при дальнейшем добавлении лаговых значений X очередное изменении z* будет меньше некоторого наперед заданного числа. Затем по МНК оценивается уравнение регрессии.

и из всех возможных значений Л выбирается то, при котором коэффициент детерминации R² регрессии (171) будет наибольшим. Найденные таким образом параметры а, Р₀ и Л подставляются в уравнение (169). Возможности современных компьютеров позволяют провести указанные расчеты за приемлемое время.

Однако более распространенной является схема вычислений, получившая название по фамилии автора метода: преобразование Койка.

Суть метода заключается в следующем.

Вычитая из уравнения (169) такое же уравнение для предыдущего периода (f -1), но умноженное на Л, т. е.

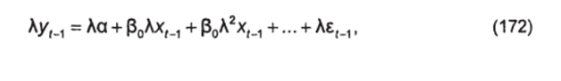
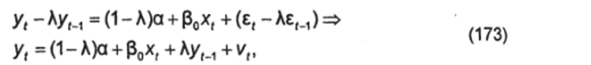
где v_t-t_t- Ае_м — скользящая средняя между остатками ?, и е_м.

Преобразование по данному методу уравнения (169) в уравнение (173) и называется преобразованием Койка.

Отметим, что с помощью указанного преобразования уравнение с бесконечным числом лагов (с убывающими по степенному закону коэффициентами) преобразовано в авторегрессионное уравнение, для которого требуется оценить лишь три коэффициента: А, а, (3₀. Это, кроме всего прочего, снимает одну из острых проблем моделей с лагами — проблему мультиколлинеарности.

Модель (173) позволяет анализировать краткосрочные и долгосрочные свойства переменных.

В краткосрочном периоде можно значение у_м рассматривать как фиксированное и краткосрочный мультипликатор считать равным (3₀.

Долгосрочный мультипликатор вычисляется по формуле суммы бесконечно убывающей геометрической прогрессии. Если предположить, что в долгосрочном периоде x_t стремится к некоторому своему равновесному значению х*, то значения у* и у_м также стремятся к своему равновесному значению у*. Тогда без учета случайного отклонения уравнение (173) примет вид.

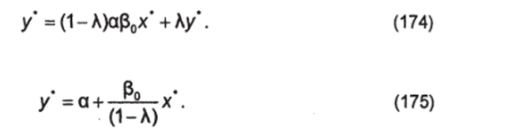
Вследствие формулы для суммы бесконечно убывающей геометрической Следовательно, прогрессии = Р₀+Р₀А + Р₀А²+ Р₀А³+… и, значит, полученная дробь яв;

(1-А) ляется мультипликатором, который отражает долгосрочное воздействие X на У. Очевидно, что при 0 < А < 1 долгосрочное воздействие будет сильнее кратко;

о срочного, т. к. > Ро.

(1-А) Вместе с тем необходимо иметь в виду, что при применении преобразования Койка оценки, полученные по МНК, могут оказаться смещенными и несостоятельными, поскольку:

• ? среди объясняющих переменных появляется переменная у_м, которая, в принципе, носит случайный характер, что нарушает предпосылки Гаусса-Маркова. Кроме того, данная объясняющая переменная наверняка коррелирует со случайным отклонением v_t;
• ? если для случайных отклонений исходной модели выполняется

предпосылка об отсутствии автокорреляции, то для случайных отклонений v_t она, скорее всего, имеет место.

Для выявления автокорреляции в уравнении с лаговой зависимой переменной в качестве объясняющей вместо обычной статистики DW ДарбинаУотсона необходимо использовать так называемую Л-статистику Дарбина.

Модифицированная статистика Дарбина-Уотсона, или h-статистика Дарбина для предполагаемого регрессионного уравнении рассчитывается по формуле.

где р — оценка коэффициента автокорреляции первого порядка в остаточной последовательности e_f;

D (g) — выборочная дисперсия при лаговой объясняющей переменной у_м; п — число наблюдений.

Дисперсию D (g) можно оценить по квадрату стандартной ошибки S_ff для коэффициента Л перед лаговой переменной у_м в оцениваемом уравнении (173). Трудность вычисления статистики h, однако, заключается в невозможности ее расчета при nD (g) > 1.

При достаточно большом объеме выборки (п > 20) нуль-гипотезу Но. р = 0, т. е. об отсутствии автокорреляции, проверяют по нормальному распределению с заданной доверительной вероятностью (обычно 0,05). Если h>u (0,05), где и — аргумент функции Лапласа, то существование автокорреляции считается доказанным и возникает необходимость ее устранения.

Устранение означает переход модели, в которой остаточная последовательность подчиняется предпосылкам МНК, в первую очередь, о некоррелированности ее членов и равенстве нулю их математического ожидания.

Предположим, что в автокорреляционной функции для у_{, т. е. в последовательности значений r_t, рассчитываемых по соотношению (163), значимым признан только коэффициент r_v Это дает основание считать остаточную последовательность подверженной автокорреляции первого порядка. Иначе говоря, имеет место соотношение.

в котором случайная составляющая v_t удовлетворяет предпосылкам МНК. Таким образом, если есть уверенность в автокорреляции только первого порядка и известна оценка р для коэффициента в уравнении (177), автокорреляцию можно устранить и получить оценки регрессии в модели с бесконечным числом лагов. В этом и состоит суть авторегрессионного преобразования.

Поясним его на модели линейной парной регрессии.

Вычтем из (178) такое же уравнение, построенное для момента (f- 1) и умноженное на известный коэффициент р (осуществим авторегрессионное преобразование AR1):

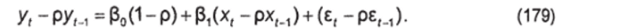
Учтя далее равенство (177) и обозначив 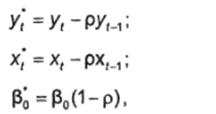получим регрессионное уравнение:

для которого выполняются все предпосылки МНК. Следовательно, можно рассчитать оценки для коэффициентов которые будут наилучшими линейными оценками.

В принципе изложенная схема может быть обобщена на автокорреляцию более высокого порядка, т. е. получены преобразования AR (2), AR (3) и т. д.

Отметим, что в AR1 для расчета оценки р можно прибегнуть к обычной статистике Дарбина-Уотсона, поскольку из соотношения (104) следует, что.

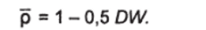
По методу Хилдрвта-Лу регрессия (179) оценивается для каждого возможного значения р из отрезка [-1, 1] с любым шагом (например, 0,001; 0,01 и т. д.). Величина, дающая наименьшую стандартную ошибку регрессии, принимается в качестве оценки коэффициента авторегрессии. После этого значения PJ и PJ оцениваются из уравнения регрессии (180) именно с данным значением.

Этот итерационный метод широко используется в пакетах прикладных программ.

В случае, когда есть основание считать, что автокорреляция отклонений очень велика, можно использовать упоминавшийся выше метод первых разностей.