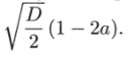Распространение фронтов, импульсов и волн

Распространение волны в системах с диффузией

В популяционной генетике к задаче распространения волны приводит рассмотрение области, занятой особями — носителями доминантного гена. Подобные задачи встречаются в экологии при изучении распространения вида. Эффекты, возникающие при распространении волн в активной кинетической среде, играют особую роль в процессах передачи информации и управления в биологических системах.

Рассмотрим дифференциальное уравнение.

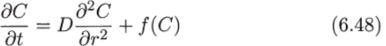
с начальным условием.

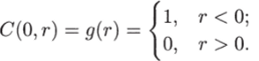
Начальное условие такого вида означает, например, что обширная территория (в одномерном случае — полупрямая г < 0) занята доминантным геном, концентрация которого близка к единице. В начальный момент времени область, где С = 1, имеет резкую границу, и при всех г > 0 концентрация (7 = 0. При.

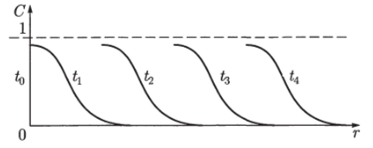
Рис. 6.7. Профиль плотности С в зависимости от координаты г в последовательные моменты времени: t-i > 4з >² > t >.tо = О.

t = 0 наминается распространение «волны» ненулевых концентраций доминантного гена в область г > 0, которое является следствием взаимодействия двух процессов: случайного перемещения особей (диффузии частиц) и размножения, описываемого функцией /©. Эти процессы ведут к перемещению области плотностей, близких к единице, с возрастанием t слева направо. Примерная картина профиля плотности С в зависимости от координаты г в разные моменты времени изображена на рис. 6.7.

В начальный момент времени to — 0 кривая имеет вид ступеньки. С течением времени фронт волн перемещается вправо, причем его форма приближается к определенной предельной кривой. А. Н. Колмогоров, И. Г. Петровский и Н. С. Пискунов [А. Н. Колмогоров и [др.], 1975] решили задачу (1937) о предельной скорости перемещения фронта волны и определили предельную форму фронта. В качестве функции /© в этой работе рассматривали функцию, равную нулю при С = 0 ч С — 1 и положительную в промежуточных точках. Вид такой функции показан на рис. 6.8, а.

Сделанные относительно /© предположения означают, что при малых С концентрация резко нарастает за счет функции размножения /©. При дальнейшем возрастании С функция }(С) — скорость роста концентрации С — начинает убывать, и при С, близких к единице, наступает насыщение. Изменение вида функции C (t) в зависимости от времени в фиксированных точках пространства г* изображено на рис. 6.9.

Рис. 6.8. Возможные типы функции /© для уравнения (6.48).

Продолжительность лаг-периода (времени запаздывания роста) функции C (r, t) зависит от координаты г. Как только благодаря диффузии малые, но конечные концентрации достигли точки г*, начинается бурный рост С до значений, близких к единице, в соответствии с функцией f©. Таким образом, малые концентрации, которые распространяются за счет диффузии, увеличиваются за счет нелинейных свойств локальной системы. Взаимодействие этих двух процессов приводит к тому, что волна концентрации, близкой к единице, движется слева направо (см. рис. 6.9). В работе [А. Н. Колмогоров и [др.], 1975] установлено, что предельная скорость распространения фронта волны для функции, изображенной на рис. 6.8, а, равна:

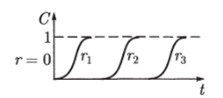
Рис. 6.9. Вид функции C (t) в фиксированных точках пространства.

Чтобы найти предельную форму фронта распространения концентраций, вводят так называемую автоволновую переменную: z = г — и ищут решение уравнения (6.48) в виде.

Предельная форма кривой плотности задается решением уравнения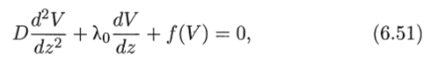

которое обращается в нуль при z = -hoc и в единицу при z = —оо. Такое решение V (z) всегда существует и единственно с точностью до преобразования z' — z + А (А — произвольная постоянная), не меняющего форму кривой.

Автоволновое решение (6.50) обладает тем свойством, что при изменении t форма кривой, изображающей зависимость V(?), не меняется, а сама эта кривая перемещается слева направо со скоростью X. Можно показать, что уравнение (6.50) имеет решение, удовлетворяющее граничным условиям при z —> ±оо, лишь при X = Хо (формула (6.49)). За счет множителя у/ f{0) скорость распространения волны (6.49) может быть существенно больше, чем скорость, с которой распространяются не очень малые концентрации за счет диффузии. Эго увеличение скорости распространения происходит вследствие действия «размножителя», функционирование которого описывается точечной (локальной) системой.

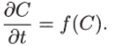
В ряде моделей возникают функции иного вида, чем изображенные на рис. 6.8, а. Например функция на рис. 6.8, б описывает случай, когда размножение частиц начинается не при любой сколь угодно малой концентрации, а только при достижении некоторой достаточно большой концентрации Со- Такая функция встречается в некоторых моделях химической кинетики и моделях передачи сигналов в биологических системах, когда реакция начинается только в том случае, когда концентрация достигает порогового значения. Эта функция также применяется в теории горения, пороговое значение переменной величины здесь имеет смысл температуры возгорания. В случае когда начальное условие задано «ступенькой» (см. рис. 6.8, б), в распределенной системе также распространяется концентрационная волна.

Случай, изображенный на рис. 6.8, в, встречается в ряде задач популяционной генетики и экологии. Отрицательность функции /© при малых С описывает, например, эффект, связанный с тем, что при малой концентрации скорость размножения мала, так как мала частота встреч особей разного пола. Поэтому за счет смертности при малых С скорость изменения численности отрицательна. Именно такой вид функции скорости роста был рассмотрен в гл. 4 (см. рис. 4.10, б) при изучении популяций с наименьшей критической численностью. В случае, представленном на рис. 6.8, в, для распространения концентрационной волны постоянной амплитуды нужно еще потребовать, чтобы величина 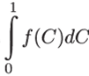¹ была положительна, в противном случае будет распространяться область малых значений концентраций.

В важном частном случае f (C) = С (С — 1)(а — С) скорость волны, которая устанавливается при больших t, можно вычислить явно. Именно этот тип функции используется в уравнении Фитцхью —Нагумо для описания распространения нервного импульса. Модель этого чрезвычайно важного для биологии явления будет рассмотрена в 6.4.2. В этом случае скорость распространения волны оказывается равной