Многомерная случайная величина. 
Статистическая независимость

Пусть состояние системы, кроме величины X, характеризуется еще одной физической величиной У, которая также, как и величина X, является однозначной функцией состояния системы: У = У (|). Совокупность {X, Y} двух случайных величин называется двухмерной случайной величиной. Все определения и формулы предыдущего раздела можно использовать для статистического описания дискретной случайной величины У и двухмерной величины {X, У}. Так, согласно формуле (2.6) вероятность W (t, Y) того, что одна произвольно выбранная система ансамбля в момент времени t находится в состоянии, которое соответствует заданному значению У, определяется как.

где N (t, У) — число систем ансамбля, для которых величина У в момент времени t принимает заданное значение У. Следует заметить, что функции W (t, X) и W (t, У) могут отличаться друг от друга не только своими аргументами. В общем случае это две различные функции. Если в первой функции заменить аргумент X на У, то получим функцию, которая, вообще говоря, не совпадает с функцией W (t, У) распределения величины У. Однако в любом случае функция W (t> У) так же, как и функция W (t_} X), удовлетворяет условию нормировки.

Пусть N (t_} X, У) есть число систем ансамбля, находящихся в момент времени t в состояниях с заданными значениями X и У. Очевидно, что.

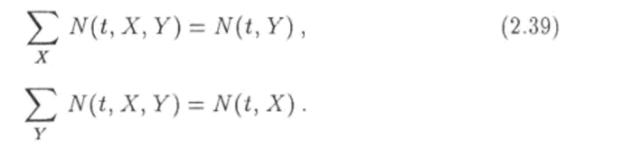
Предел отношения числа N (t_y X. У) к числу N систем в ансамбле при неограниченном увеличении последнего есть вероятность того, что одна какая-то система ансамбля находится в момент времени t в состоянии, которое соответствует заданным значениям X и У:

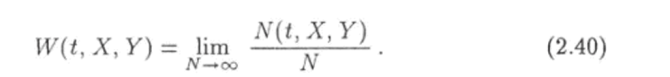
Зависимость W = W (t, X, У) называется функцией распределения двухмерной случайной величины {X, У}.

Просуммируем обе части равенства (2.40) по всем значениям величины X. С учетом соотношений (2.37) и (2.39) получим:

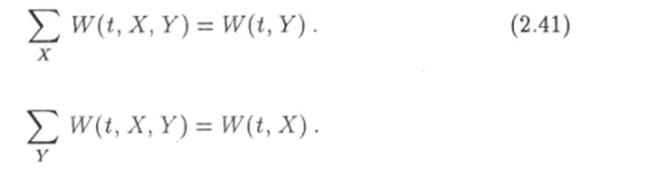
Суммирование обеих частей равенства (2.41) по всем значениям У с учетом (2.38) приводит к условию нормировки Аналогично.

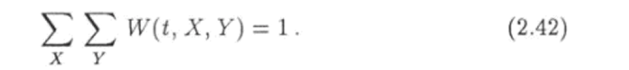
Все системы ансамбля, которые находятся в состояниях, соответствующих одному и тому же значению У, в свою очередь образуют ансамбль, который называется подансамблем. Число систем в этом ансамбле равно N (t_y У). Среди систем подансамбля N (t, Х_} У) систем находятся в состояниях с заданным значением X. Поэтому согласно принятому определению вероятности предел отношения числа N (t, X, Y) к числу N (t, Y) систем в подансамбле при неограниченном возрастании последнего.

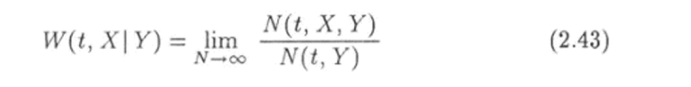
есть вероятность того, что одна из систем ансамбля находится в состоянии с заданным значением X, но при условии, что рассматриваются только такие системы, для которых величина У равна вполне определенному значению У. Но этой причине вероятность W (t_y Х У) называется условной вероятностью.

Из определений (2.37), (2.40) и (2.43) вытекает соотношение.

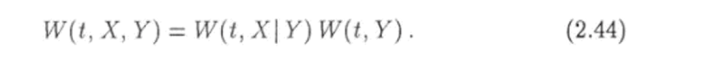
Случайные величины X и У называются статистически независимыми, если каждая из них принимает то или иное значение вне зависимости от того, какое значение имеет другая величина. Если величины X и У статистически независимы, то число систем, находящихся в состояниях с заданным значением X, должно быть пропорционально полному числу систем в ансамбле независимо от того, какое значение принимает для этих систем величина У:

aside class="viderzhka__img" itemscope itemtype="http://schema.org/ImageObject">

В пределе при N —*? оо будем иметь Подстановка (2.45) в (2.44) дает.

Таким образом, для статистически независимых случайных величин их общая функция распределения равна произведению функций распределения каждой их этих величин в отдельности.

Среднее значение некоторой величины /, зависящей от Л' и У: / = f (X_} У), определяется формулой.

В частности, среднее значение произведения X У есть.

Для статистически независимых величин в силу соотношения (2.46) будем иметь.

т.е. среднее значение произведения статистически независимых случайных величин равно произведению их средних значений.

Пусть состояние системы характеризуется двумя величинами хит/, имеющими непрерывный спектр значений. Теперь для статистического описания системы следует использовать плотность вероятности.

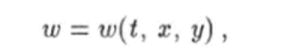
смысл которой заключается в том, что выражение.

есть вероятность того, что в момент времени t система находится в состоянии, для которого значение величины х принадлежит интервалу (х, х + с/х), а значение у — интервалу (у, у 4- dy).

Если выражение (2.50) проинтегрировать по всем возможным значениям х, то получим вероятность w (t, у) dy того, что значение величины у принадлежит интервалу (у, у + с/у). После сокращения на dy получим:

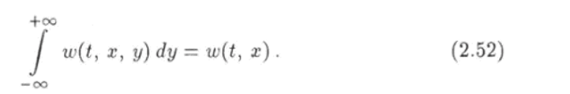
где w (t, у) — функция распределения величины у. Нетрудно заметить, что формула (2.51) является аналогом формулы (2.41). Аналогично можно записать Вообще, все формулы и соотношения, полученные для функций от дискретных случайных величин, можно применять для непрерывных случайных величин с тем только отличием, что суммирование следует заменить интегрированием. Так вместо условия нормировки (2.42) теперь будем иметь следующее условие:

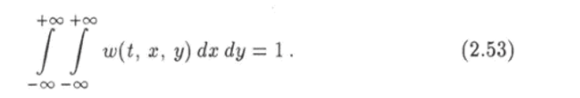
Два знака интеграла в левой части этого равенства означают, что интегрирование производится по двум переменным: х и у. Такие интегралы называются кратными. Условие нормировки (2.53) можно вывести из равенства (2.52), если проинтегрировать обе его части по х и использовать условие (2.19).

Среднее значение / функции / = /(х, у) двух случайных величин х и у определяется формулой.

Для статистически независимых случайных величин хну плотность вероятности w (i, х, у) равна произведению плотностей w (f, х) и w (t, у):