Составная труба под внутренним давлением

Предположим, что необходимо повысить давление в трубе, не изменяя ее внутреннего диаметра и не переходя к другому материалу.

Как показано выше, увеличение наружного диаметра трубы неэффективно.

Рассмотрим решение этого вопроса на примере трубы, изготовленной из кислотостойкой хромоникелевой стали 1Х18Н9Т, для которой? = 2 • 10⁵ МПа, ст_г = 260 МПа. Примем внутренний радиус трубы а = 20 мм, наружный с = = 50 мм. Труба должна выдерживать без появления пластических деформаций внутреннее давление, равное р_а = 130 МПа.

Наиболее напряженными будут точки, прилегающие к внутренней поверхности трубы (г = а). Если воспользоваться гипотезой максимальных касательных напряжений, в этих точках условие пластичности примет вид ст._ж" = ст, — а, < [ст].

Учитывая выражения (2.28), получим.

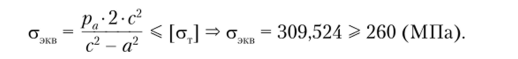
Следовательно, при заданных условиях требуются какие-то конструктивные или технологические решения, которые бы повысили прочность трубы.

Одним из таких возможных решений является переход к составной трубе.

Берется вторая труба из того же материала, для которой внутренний радиус несколько меньше наружного радиуса первой трубы, пусть он будет равен с — б. Затем вторая труба нагревается так, чтобы первая свободно вставлялась во вторую.

При остывании вторая труба «обжимает» первую, па поверхности контакта появится контактное давление (р_к), которое для первой трубы будет сжимающим наружным, а для второй — внутренним растягивающим. В результате напряжения в первой трубе перераспределяются и составная труба воспринимает большее давление.

Проведем соответствующие вычисления.

Пусть вторая труба, радиусы которой равны 20 — 5, b = 80 мм, нагрета так, что 8 = 0,024 мм.

После остывания конструкции наружный радиус первой трубы получит отрицательной перемещением,(г = с), а внутренний радиус второй — положительное перемещение и₂(г = с). Их разность должна быть равна 8, т. е.

Воспользовавшись формулой (2.22), выпишем выражения для этих перемещений:

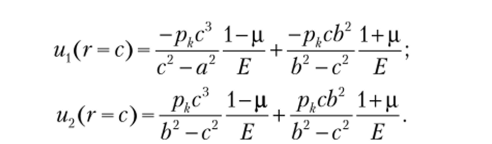
Подставим их в формулу (2.29). В результате получим выражение для контактного давления.

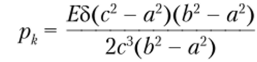
Таким образом, составная труба еще до приложения внутреннего давления находится в напряженном состоянии «натяга», которое иллюстрируется графиками на рис. 2.8.

Рис. 2.8.

Если предварительно ненапряженную трубу с радиусами а = 20 мм, b = = 80 мм нагрузить требуемым внутренним давлением (р₍₁⁼ 130 МПа), то напряжения, рассчитанные, но формулам (2.23), будут равны (рис. 2.9).

Складывая эти напряжения с напряжениями натяга, получим напряжения в составной трубе при действии заданного внутреннего давления (рис. 2.10).

Рассчитав эквивалентные напряжения в наиболее напряженных точках труб, обнаруживаем, что при принятом зазоре (5 = 0,024 мм) а_экв(г = 20) = = а, — а₃ = 214,93 МПа, а_экв(г = 51) = 125,326 МПа. Таким образом, максимальные эквивалентные напряжения меньше предела текучести материала и составная труба воспринимает внутреннее давление р₍= 130 МПа без появления пластических деформаций, при этом коэффициент запаса равен и_т = а_т/а_экв(г = 20) = 260/214,93 = 1,21.

Рис. 2.9 Рис. 2.10

Однако полученное напряженное состояние составной трубы нс является оптимальным: внутренняя труба перенапряжена, а наружная недонанряжена. Можно подобрать такой зазор 5, при котором обе трубы станут равнопрочными.

Расчеты показывают, что при 5 = 0,0388 мм максимальные эквивалентные напряжения в обеих трубах будут равны 176,35 МПа, а п_т = 1,47.

Эта задача была решена профессором Михайловской артиллерийской академии А. В. Гадолиным при разработке методов расчета на прочность многослойных стволов орудий. Формулы Ламе при этом получались как частный случай.