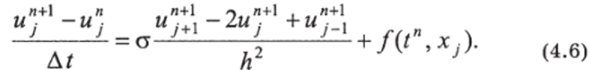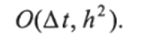Неявная разностная схема

Характеристика неявной разностной схемы

<

/b>Рассмотрим одномерное дифференциальное уравнение параболического типа с начальным и граничными условиями:

Запишем для уравнения (4.5) неявную разностную схему:

Запишем аппроксимацию начального и граничных условий:

Аппроксимация граничных условий (4.7) записана на (п + 1)-м шаге по времени для удобства последующего изложения метода и алгоритма решения неявной разностной схемы (4.6).

В разделе 2.3.3 было отмечено, что разностная схема (4.6) имеет такой же порядок аппроксимации, как и соответствующая ей явная разностная схема (4.2), а именно:

В разделе 3.4 было доказано, что неявная разностная схема (4.6) абсолютно устойчива, т. е. вне зависимости от выбора интервала деления на разностной сетке (или, иначе говоря, выбора расчётного шага по независимым переменным) погрешность решения неявной разностной схемы в процессе вычислений возрастать не будет. Отметим, что это, безусловно, является достоинством неявной разностной схемы (4.6) по сравнению с явной разностной схемой (4.2), которая устойчива только при выполнения условия (3.12). В то же время явная разностная схема имеет достаточно простой метод решения, а метод решения неявной разностной схемы (4.6), называемый методом прогонки, более сложен.