Критерии оптимальности планов

Типы планов эксперимента

Построение плана эксперимента можно интерпретировать как выбор строк матрицы X, их числа и последовательности проведения. Этот выбор осуществляется разными способами и соответственно приводит к различным результатам, поэтому коэффициенты могут быть оценены с разной точностью и иметь разные ковариации, а предсказанные значения отклика получатся с разными дисперсиями. В зависимости от того, какие требования экспериментатор предъявляет к модели, он может прийти к той или иной формулировке требований к матрице X. Формализация этих требований связана с критериями оптимальности, которые удобно формулировать в терминах свойств матрицы или матрицы М = Х‘Х. Именно они непосредственно связаны с оценками модели и функционально зависят от матрицы X. Так, например, при диагональной матрице М план оказывается ортогональным, т. е. все столбцы матрицы X взаимно ортогональны и коэффициенты модели независимы: cov{b_f, ЬД = 0.

В настоящее время используется свыше 20 различных критериев оптимальности планов эксперимента, которые подразделяются на две основные группы. К первой группе относят критерии, связанные с ошибками оценок коэффициентов, а ко второй — с ошибкой оценки поверхности отклика. Далее охарактеризуем только те критерии, которые наиболее часто применяются при решении задач оптимизации, описания поверхности отклика и оценки влияния факторов.

1. Критерий D-оптимальности, принадлежащий первой группе, представляет интерес для задач оптимизации, выделения доминирующих параметров на начальных этапах решения оптимизационных задач или для выявления несущественных параметров в задачах восстановления закономерности функционирования объекта. Геометрическое истолкование свойств ошибок коэффициентов связано со свойствами эллипсоида их рассеяния (также и доверительного эллипсоида), определяемого математическим ожиданием и дисперсией значений ошибок. Пространственное расположение, форма и размер эллипсоида полностью зависят от плана эксперимента.

Доверительный эллипсоид для вектора коэффициентов размерности к -Г 1 имеет вид.

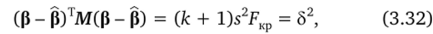
где М = Х^ТХ — информационная матрица плана (обратная к ковариационной), s² — оценка дисперсии ошибок наблюдений с числом степеней свободы.

e, F_Kp — квантиль уровня, а распределения Фишера с числом степеней свободы ср_г = к + 1 и Ф₂ = ср_е, Р — вектор оценок коэффициентов уравнения регрессии.

Эллипсоид (3.32) с вероятностью 1 — а накрывает точку истинных значений коэффициентов. На рис. 3.14 приведен пример доверительного эллипсоида для двумерного случая. Объем доверительного эллипсоида пропорционален квадратному корню из определителя ковариационной матрицы.

Этот критерий требует такого расположения точек в области планирования, которое соответствует минимальному.

Рис. 3.14. Доверительный эллипсоид для двумерного случая для критерия D-оптимальности.

объему эллипсоида рассеяния ошибок (минимум произведения всех дисперсий коэффициентов полинома), т. е. определитель матрицы С должен быть минимальным. В соответствующем плане эффекты факторов максимально независимы друг от друга. D-оптимальный план минимизирует ожидаемую ошибку предсказания функции отклика.

• 2. Критерий А-оптимальности требует такого выбора плана, при котором матрица С имеет минимальный след (сумма диагональных элементов матрицы С минимальна). Так как диагональные элементы матрицы С пропорциональны дисперсиям оценок коэффициентов, то критерию А-оптимальности соответствует план с минимальной суммарной дисперсией всех коэффициентов модели.
• 3. Критерий Е-оптимальности, ему соответствует план, в котором максимальная дисперсия коэффициентов будет минимальна.

Выбор критерия зависит от задачи исследования. Так, при изучении влияния отдельных факторов на поведение объекта применяют критерий Е-оптимальности, а при поиске оптимума функции отклика — D-оптимальности. Если построение D-оптимального плана вызывает затруднения, то можно перейти к А-оптимальному плану, построение которого осуществляется проще.

Критерии второй группы используются при решении задач описания поверхности отклика, определения ограничений на значения параметров. Основным здесь является критерий G-оптимальности.

4. Критерий G-оптимальности требует такого плана эксперимента, при котором достигается минимальное значение максимальной дисперсии оценки функции отклика. Применение G-оптимального плана дает уверенность в том, что в области планирования нет точек с чрезмерно большой ошибкой описания функции отклика. В отличие от критериев А- и D-оптимальности, связанных с точностью нахождения коэффициентов, критерий G-оптимальности требует максимальной точности оценки зависимой переменной.

Среди всех классов планов основное внимание в практической работе уделяется ортогональным и ротатабельным планам.

5. Критерий ортогональности требует план, для которого выполняется условие парной ортогональности столбцов матрицы независимых переменных, т. е. для него информационная матрица М диагональна.

Матрица М является матрицей системы нормальных уравнений, из решения которой находятся оценки коэффициентов модели.

Использование критерия ортогональности имеет целью упрощение вычислений и получение независимых оценок коэффициентов. Легко видеть, что при ортогональном планировании матрица С является диагональной, следовательно, ковариации оценок коэффициентов равны нулю, т. е. коэффициенты полинома определяются независимо друг от друга. Это значит, что вычеркивание (замена нулем) любого коэффициента в уравнении модели или, наоборот, добавление слагаемых в функцию отклика не изменяет значений оценок остальных коэффициентов полинома. Такое свойство ортогональных планов оказывается очень полезным, когда точный вид модели неизвестен и исследователь использует экспериментальные данные для отбора переменных, существенно влияющих на выходную величину. Для ортогональных планов эллипсоид рассеяния ориентирован в пространстве так, что направления его осей совпадают с направлениями координат пространства факторов.

6. Критерий ротатабельности требует такого расположения экспериментальных точек в области планирования, при котором дисперсия оценки функции отклика в точке х зависит только от расстояния этой точки до центра плана. Использование ротатабельных планов обеспечивает для любого направления от центра эксперимента равнозначность точности оценки функции отклика (постоянство дисперсии предсказания) на равных расстояниях от центра эксперимента. Это особенно важно при решении задач, связанных с поиском экстремальных значений функции отклика, когда исследователь до начала экспериментов не знает, в каком направлении надо двигаться, чтобы найти экстремум функции отклика, и поэтому стремится принять план, точность которого одинакова во всех направлениях.

Критерии 5 и 6 обеспечивают некоторые полезные и удобные свойства оценок коэффициентов, однако они никак не связаны с требованием максимальной точности построения модели. Различные критерии этой группы приведены в табл. 3.17. В таблице каждый критерий определяется тремя различными, но эквивалентными способами.

Таблица начинается с критерия D-оптимальности, с названием которого часто связывается вся концепция оптимального построения планов. Смысл его заключается в минимизации дисперсий всех коэффициентов регрессии, рассматриваемых как нечто единое, как вектор. Дисперсию вектора коэффициентов принято называть обобщенной дисперсией, которая задается известной функцией от матрицы дисперсий-ковариаций — определителем. Чем меньше определитель, тем меньше обобщенная дисперсия. Как всегда в математике, наряду с алгебраическим представлением можно использовать и геометрическое. Однако в этом случае вместо уже знакомого факторного пространства приходится вводить пространство параметров, в котором координатные оси задаются значениями коэффициентов регрессии.

Между размерностями факторного пространства и пространства параметров не существует однозначной связи. В случае одного фактора и линейного уравнения регрессии простТаблица 3.17. Критерий оптимальности планов для оценок коэффициентов модели.

ранство параметров будет двумерным (два коэффициента Ь₀, Ь_г). Если число факторов и вид уравнения заданы, тогда размерность пространства параметров определяется однозначно. Так, для линейного уравнения с к факторами пространство параметров имеет размерность к + 1. Каждой точке в таком пространстве соответствует вектор оценок коэффициентов, а определитель матрицы дисперсий-ковариаций пропорционален объему эллипсоида рассеяния оценок параметров. Причем центр эллипсоида совмещен с МНК-оценкой. Эллипсоид является многомерным аналогом обычного доверительного интервала. Для одномерного пространства параметров он вырождается в отрезок. Для двухмерного — в эллипс. Эллиптическая форма доверительного интервала связана с предпосылкой регрессионного анализа о нормальном распределении.