Устойчивое оценивание параметров управляемых объектов
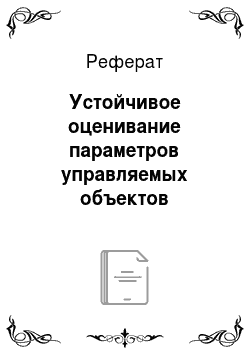
Где — -мерный вектор состояния, — -мерный вектор управления, — -мерный вектор шума объекта с нулевым математическим ожиданием и ковариационной матрицей. Воскобойников Ю. Е., Преображенский Н. Г., Седельников А. И. Математическая обработка эксперимента в молекулярной газодинамике. -Новосибирск: Наука, 1984. -240 с. В сформулированных выше условиях на основании методов теории некорректно… Читать ещё >
Устойчивое оценивание параметров управляемых объектов (реферат, курсовая, диплом, контрольная)
Устойчивое оценивание параметров управляемых объектов
В последнее время в связи с предъявлением все более высоких требований к процессам управления в различных областях техники проблема идентификации становится исключительно важной. Нельзя обеспечить качественное управление системой, если ее математическая модель не известна с достаточной точностью. Для построения математической модели могут быть использованы как теоретические, так и экспериментальные методы. Известно, что нельзя построить математическую модель, адекватную реальной системе, только на основе теоретических исследований физических процессов в системе. Сформированная таким образом математическая модель, как правило, значительно отличается от реальной системы, что приводит соответственно к снижению качества управления. Поэтому в процессе проектирования систем управления одновременно с теоретическими исследованиями проводятся многочисленные эксперименты по определению и уточнению математической модели системы. Определение всех характеристик процесса, модель которого нужно построить, не является, вообще говоря, не только возможным, но даже и желательным. Характеристики, знать которые необходимо, определяются целью, поставленной перед системой, допустимой степенью сложности системы в целом и требованиями к сопутствующим вычислительным процедурам.
Широко распространены алгоритмы идентификации [1,2], основанные на методе наименьших квадратов, который обеспечивает получение среднеквадратических оценок параметров. Эти методы пригодны и для нестационарных процессов с медленно меняющимися параметрами. Они могут использоваться для построения части модели вход-выход-шум, а также для оценки неизвестных параметров заданных нелинейных функций или полиномиальных аппроксимаций неизвестных нелинейных функций. Регрессионные методы позволяют проводить идентификацию при одновременных воздействиях на нескольких входах системы и, могут быть представлены в рекуррентной форме. Перечисленные обстоятельства свидетельствуют об эффективности методов идентификации с помощью регрессионных методов.
Рассмотрим линейную дискретную динамическую систему вида:
(1).
где — -мерный вектор состояния, - -мерный вектор управления, — -мерный вектор шума объекта с нулевым математическим ожиданием и ковариационной матрицей .
Введем следующие обозначения.
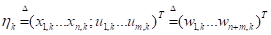
.
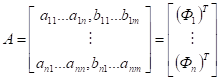
.
Следовательно, уравнение (1) запишется в виде.
.
Тогда для оцениванияй строки матрицы можно использовать выражение вида.
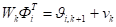
(2).
Где.
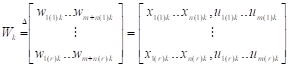
.
.
В тех случаях, когда отсутствуют сведения об априорном распределении, рекомендуется в качестве оценки вектора брать такое значение, которое с наибольшей вероятностью обусловливает появление именно заданного вектора. При нормальном распределения вектора шума измерения с нулевым средним и ковариационной матрицей оценка максимального правдоподобия находится из системы алгебраических уравнений.
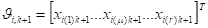
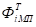
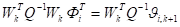
(3).
и является несмещенной и эффективной при конечном объеме измерений [1,3].
Несмотря на хорошие статистические свойства, применение оценки очень ограниченно. Это связано с плохой обусловленностью матрицы, что при отсутствии априорных ограничений на значение вектора вызывает большие ошибки оценивания вектора. Более того, матрицы и имеют худшую обусловленность, чем матрица исходного уравнения (2), поэтому при решении (3) возможно проявление численной неустойчивости, заключающейся в том, что малые погрешности в исходных данных могут вызвать конечные, но неприемлемые по величине ошибки решения.
В сформулированных выше условиях на основании методов теории некорректно поставленных задач [4,5] регулярное решение уравнения (3) можно записать в виде:
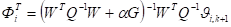
.
где — положительно определенная матрица, — параметр регуляризации.
Матрицу, например, можно выбирать в виде:
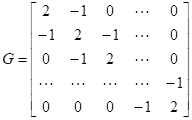
.
Здесь параметр регуляризации целесообразно определять как корень следующего нелинейного уравнения:
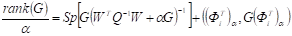
.
Рассматривался также минимаксный вариант решения рассматриваемой задачи на основе различных способов задания «множества корректности», минимизирующего среднеквадратическую ошибку решения уравнения (2).
Для решения уравнения (2) можно также применить методы и алгоритмы калмановской фильтрации [6,7]. Тогда модель динамического процесса, соответствующего уравнению (2), определится уравнениями.
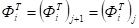
.
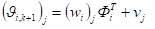
.
где — -ая строка матрицы .
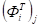
Из общих уравнений фильтра Калмана [6,7] следует, что оценка, минимизирующая среднеквадратическую ошибку оценивания, определяется рекуррентными соотношениями.
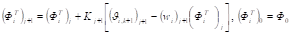
.
.
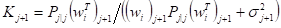
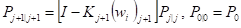
.
гдедисперсия шума измерения вх точках,.
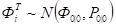
.
Практическая реализация приведенных выше алгоритмов на основе разработанного программного обеспечения показала свою эффективность при решении разнообразных задач идентификации и управлении промышленными объектами.
Гроп Д. Методы идентификации систем. — М.: Мир, 1979. — 302 с.
Штейнберг Ш. Е. Идентификация в системах управления. -М.: Энергоатомиздат, 1987. — 80 с.
Кашьяп Р.А., Рао А. Р. Построение динамических моделей по экспериментальным данным. Пер. с англ. — М.: Наука, 1983. — 384 с.
Тихонов А.Н., Арсенин В. Я. Методы решения некорректных задач. — М.: Наука, 1979. — 288 с.
Воскобойников Ю.Е., Преображенский Н. Г., Седельников А. И. Математическая обработка эксперимента в молекулярной газодинамике. -Новосибирск: Наука, 1984. -240 с.
Фильтрация и стохастическое управление в динамических системах. / Под ред. К. Т. Леондеса. Пер. с англ., — М.: Мир, 1980. — 407с.
Браммер К., Зиффлинг Г. Фильтр Калмана — Бьюси. — М.: Наука, 1982. — 200 с.