Поиск нетривиальных следствий и допущений

Относительно любой нейтральной в логическом отношении формулы каноническими будут два следующих вопроса: что из нее следует с необходимостью? какие допущения достаточны для ее истинности? Ответ на первый вопрос дает приведение формулы к конъюнктивной нормальной форме, на второй — приведение формулы к дизъюнктивной нормальной форме. В этом параграфе будет показано, что для ответа на данные вопросы можно использовать метод деревьев.

Среди всех логических следствий особый интерес представляют сильные, а среди всех допущений — слабые. Теи другие можно назвать нетривиальными. Сильные следствия поглощают все слабые. Значит, зная сильные, нам всегда становятся известны слабые, но не наоборот. Слабые допущения интересны тем, что указывают минимальные условия, при которых рассматриваемая формула истинна. Поиск сильных допущений неизбежно приводит к парадоксу. Так как из лжи следует все, что угодно, то она и должна быть признана единственным допущением любого знания.

Формулы А и (A v В) обе оказываются необходимыми следствиями формулы (А & В). Но А сильнее (A v В): из А следует (A v В), однако из (A v В) не следует А. Следовательно, А — нетривиальное следствие; зная А, мы обязательно будем знать (A v В), но не наоборот. К сказанному следует добавить также требование того, чтобы сильное следствие не совпадало с посылкой исходной формулы.

Логическое следствие формулы нетривиально, если оно не поглощается никаким другим ее следствием и не эквивалентно какойнибудь ее посылке.

Формула (A v В) следует как из допущения А, так и из допущения (А & В). Но из этих допущений А более слабое: из (А & В) следует А, но обратное неверно. Следовательно, А — нетривиальное допущение. Ведь очевидно, что формулу всегда легче доказать на основании более сильного допущения, чем более слабого. Следует также добавить, что нетривиальная посылка не должна совпадать с заключением исходной формулы.

Допущение формулы нетривиально, если оно не поглощает никаких других ее допущений и не эквивалентно самой формуле.

Частным случаем задачи поиска нетривиальных допущений выступает восстановление’пропущенных посылок.

Дерево формулы, построенное согласно правилам П1-П14, позволяет эффективно находить нетривиальные следствия и допущения логически нейтральной формулы.

Допустим, сконструировано дерево исследуемой формулы. Ее необходимым следствием будет дизъюнкция любых ее конъюнктов по одного му из каждой ветви. Из них нетривиальными окажутся те, которые не поглощаются никакими другими, и те, которые не совпадают с посылкам и. Допущением формулы будет конъюнкция формул, эквивалентная любой ее полной (от вершины до основания) ветви. Из них нетривиальными будут те, которые не поглощают никаких других, и те, которые не совпадают со всей формулой.

Дана формула ((Л & ->В) & (A v С) & ->(В & С)). Необходимо найти все ее нетривиальные следствия и допущения.

Дерево формулы:

Просматривая дерево сверху вниз, обнаруживаем все необходимые следствия формулы: ->В и (Л v С). Ни одно из них не поглощает другое. Но формула (Л v С) — подформула рассматриваемой формулы. Следовательно, только следствиеiВ нетривиально.

Просматривая ветви дерева слева направо, находим все допущения формулы, в случае истинности которых она необходимо истинна: (-.В & Л) или (—iB & С). Ни одно их них не поглощает другое. Следовательно, они оба нетривиальны.

Дана формула ((Л э В) & (В э Q).

Дерево формулы: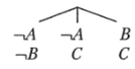

Просмотр дерева формулы по горизонтали (все комбинации по одному конъюнкту из каждой ветви) выявляет наличие одного-единственного нетривиального следствия — (-А v С). Такие следствия, как (—тЛ v В), (-1В v С), тривиальны, так как эквивалентны посылкам. Следствия (-А v -A v С), (-А v С v С), (—A v -, В v С), (~>В v В) тривиальны, поскольку поглощаются нетривиальным следствием (-И v С).

Анализ дерева формулы по вертикали позволяет найти все допущения рассматриваемой формулы: (-А & -, В), (—А & С), (В & С). Все они нетривиальны, так как ни одно из них не поглощает другие.

Следующая серия задач на поиск необходимых следствий заимствована из сочинений Р. М. Смаллиана «Как же называется эта книга?» (М., 1981), «Принцесса или тигр?» (М., 1985) и «Алиса в стране смекачки» (М., 1987).

Пример 1 (найти нетривиальное следствие) Из троих (Л, В и С) один рыцарь (всегда говорит правду), один лжец (всегда лжет) и один нормальный человек (иногда говорит правду, иногда ложь). Кто кем является, если А утверждает: «Я — нормальный человек»; В его поддерживает: «Это правда»; С называет себя ненормальным.

Пусть А_р обозначает, что Л — рыцарь, А_н — А нормальный человек, А_л — А лжец. Для остальных участников индексация такая же.

Утверждение А эквивалентно дизъюнкции (А_и v Л_л), поскольку рыцарь не может назвать себя нормальным человеком. Утверждение В эквивалентно дизъюнкции (В_р v В_и), так как в противном случае, т. е. когда В — лжец, А должен быть рыцарем, что невозможно. Утверждение С эквивалентно констатации истинности Ср, ибо лжец не мог назвать себя ненормальным человеком. Полностью условия задачи символизируются следующей формулой:

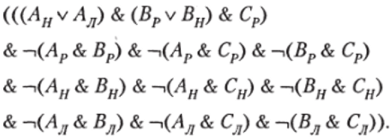
Дерево формулы:

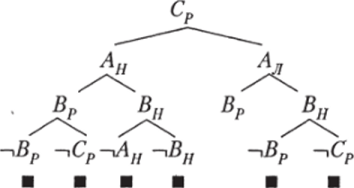
Нетривиальные следствия: (А_л & В_н & С_р), т. е. А — лжец, В — нормальный человек, С — рыцарь.

Пример 2 (найти нетривиальное следствие) Любой, кто желает жениться на принцессе, должен угадать, в какой комнате она находится. Имеется две комнаты, в каждой из которых может находиться либо принцесса, либо тигр. Это означает, что правильный выбор гарантирует свадьбу, неправильный выбор — смерть. На двери каждой комнаты висит табличка. На обеих табличках написано: «В обеих комнатах находятся принцессы». Если в первой комнате принцесса, то надпись истинная, если же тигр, то ложная. Если во второй комнате принцесса, то надпись ложная, если же тигр, то истинная.

В какой из комнат (первой или второй) принцесса, а в какой тигр, учитывая, что в одной из комнат обязательно находится принцесса, а в другой тигр?

Пусть Я, означает, что принцесса в первой комнате, Я₂ — что она во второй. Соответственно Г, означает, что тигр в первой комнате, и Т₂ — что тигр во второй. Символы -1 Я, или —IЯ₂ будут обозначать отсутствие принцессы в соответствующих комнатах, -Я, или ~, Т₂ — отсутствие тигра в соответствующих комнатах.

Условия задачи символизируется формулой:

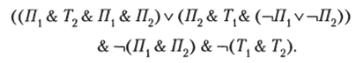aside class="viderzhka__img" itemscope itemtype="http://schema.org/ImageObject">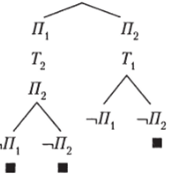

Дерево формулы:

Нетривиальные следствия: (Я₂ & Г,), т. е. принцесса находится во второй комнате, тигр — в первой.

Пример 3 (найти нетривиальное следствие) Королева Пик (КР) думает, что Король Пик (К) думает, что она не в своем уме. Кто из них в здравом уме, а кто — нет? (Находящиеся не в своем уме обо всем судят превратно.) Допустим, отсутствие знака отрицания перед буквами КР или К обозначает находящегося не в своем уме.

Сначала формализуем, что думает Король Пик:

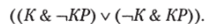
Теперь формализуем, что думает Королева Пик:

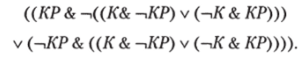
Дерево формулы: К.

Нетривиальное следствие: Король Пик не в своем уме.

Пример 4 (найти нетривиальное допущение) Командир осажденной крепости послал три следующих сообщения.

• 1. «Если нам удастся получить продовольствие, то нам не будет угрожать смерть от голода».
• 2. «Если нам не удастся получить продовольствие, то или нам будет угрожать смерть от голода, или мы попытаемся прорвать кольцо окружения».
• 3. «Если нам будет угрожать смерть от голода, то мы попытаемся прорвать кольцо окружения»^[1].

Можно ли сформулировать сообщение, эквивалентное трем указанным, но более простое в логическом смысле? Ответить на этот вопрос означает найти более простые допущения, которым были бы эквивалентны все три сообщения.

Пусть А = «Нам удастся получить продовольствие», В = «Нам не будет угрожать смерть от голода», С= «Мы попытаемся прорвать кольцо окружения». Все три сообщения символизируются следующей формулой — ((Л з В) & {-А з (-1В * С)) & (-.В з С)).

Дерево формулы:

Нетривиальные допущения: (В & А) или (В & С), т. е. все три сообщения истинны, если истинно допущение «Нам удастся получить продовольствие, и нам не будет угрожать смерть от голода» или допущение «Нам не будет угрожать смерть от голода, и мы попытаемся прорвать кольцо окружения».

Пример 5 (найти нетривиальное допущение) Путешественник попал в плен к жестоким туземцам и был поставлен перед дилеммой: умереть от яда или сгореть заживо. Чтобы сделать выбор, путешественник должен произнести только одну фразу — если при этом он скажет правду, его отравят, а если солжет — сожгут заживо. Какую фразу должен произнести путешественник, чтобы избежать смерти?

Пусть А = «умереть от яда», В = «сгореть заживо». Основные элементы ситуации выбора можно формализовать следующим образом.

Путешественник говорит «меня отравят», и это правда — (Л & (А о Л".

Путешественник говорит «меня отравят», и это ложь — (-чЛ & (-И э В)).

Путешественник говорит «меня сожгут», и это правда — (В &

(ЯэЛ)).

Путешественник говорит «меня сожгут», и это ложь — (-чВ & (-.В э В".

Все возможности выбора, учитывая, что путешественник не может в одно и то же время быть отравленным и сожженным, символизируются следующей формулой:

(Л & (Л о Л)) v (-Л & (-Л э В)) v.

v (В & (В э Л) & ч (Л & В)) v (чВ & (~iB з В)).

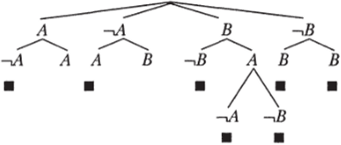
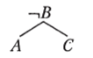
После удаления противоречивых ветвей и применения правила П12 к оставшимся дерево формулы упрощается до следующего:

Дерево формулы:

Это означает, что если путешественник произнесет «меня отравят», то независимо от того, говорит ли он правду или ложь, ему не избежать смерти: если он скажет правду, его отравят, если солжет — сожгут заживо. Следовательно, чтобы гарантированно избежать смерти, ему следует сказать «меня сожгут». Данное высказывание представляет пропущенную посылку, которую путешественнику необходимо добавить к условиям задачи, чтобы остаться в живых.

• [1] Калбертсон Дж. Т. Математика и логика цифровых устройств. — М., 1965.С. 214.