Закон распределения. 
Политический анализ и прогнозирование в 2 ч. Часть 2

Принципиально новая возможность, которой мы располагаем для параметрических переменных, — анализ формы (или закона) распределения. Он заключается в сопоставлении реального, эмпирического распределения с определенной математической моделью — теоретическим законом распределения, задаваемым некоторой функцией (как правило, функцией плотности вероятности). В качестве основной модели мы будем рассматривать уже знакомое нам нормальное распределение, функция плотности вероятности которого представляет собой колоколообразную кривую.

Анализ формы распределения чрезвычайно важен с двух точек зрения. Во-первых, очень многие статистические методы чувствительны к особенностям распределения данных. Без учета этой составляющей высок риск получить совершенно неадекватный реальности результат. Во-вторых, анализ формы распределения сам по себе может привести к важным выводам относительно содержательных особенностей изучаемых переменных.

В процессе описательно-статистического анализа параметрических данных, как и на предыдущих уровнях измерения, строится таблица и гистограмма частотного распределения. Но, в отличие от категориальных переменных, подсчет частот идет не для отдельных значений, а для равных фиксированных интервалов (этот вопрос детально рассматривался нами в главе 3).

Далее мы сопоставляем получившееся эмпирическое распределение с теоретическим. К сожалению, в программе Excel нет возможности «наложить» теоретическую кривую распределения на эмпирическую гистограмму. Такая возможность есть в профессиональных статистических пакетах, в частности в SPSS. Пример показан на рис. 6.12.

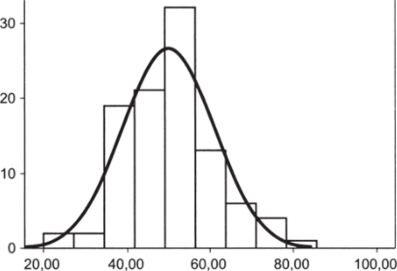
Рис. 6.12.

Наложение нормальной кривой на эмпирическое распределение — полезный, но отнюдь не необходимый инструмент. Помня ключевые свойства нормального распределения — колоколообразную форму, симметричность относительно средней и др., — можно проделать эту операцию мысленно.

На рис. 6.12 мы наблюдаем достаточно хорошее приближение эмпирического распределения к нормальному закону. С точки зрения формального статистического анализа — это хорошая новость. На практике, однако, большинство признаков, с которыми приходится работать политологам, обладают достаточно существенными отклонениями от колоколообразной кривой. В то же время именно отклонениями от нормального закона наиболее интересны и информативны с содержательной точки зрения. Научиться анализировать такие отклонения — отдельная задача, далее мы рассмотрим наиболее типичные случаи.

Во-первых, важным отклонением от нормального распределения является неоднородность исследуемой совокупности. Для однородных совокупностей характерно одновершинное (унимодальное) распределение; наличие нескольких вершин является одним из основных признаков неоднородности. В целом, однородность хорошо оценивается визуально, без специальных количественных критериев. Рассматривая гистограмму, следует задаться вопросом: можно ли естественным образом выделить в ней некоторые «геометрически самостоятельные» фрагменты?

На рис. 6.13 приведено распределение индекса институциональных основ демократии¹ для 192 стран мира. Обратите внимание, что получившееся распределение можно как бы разложить на две части, каждая из которых подчиняется.

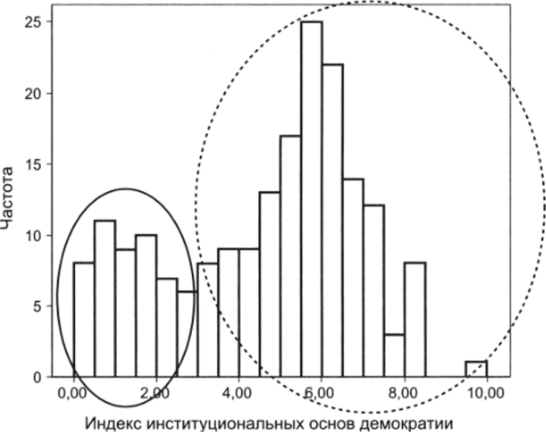
Рис. 6.13.

нормальному закону. И этому есть содержательное объяснение. В политической науке принято делить политические

'Измерение индекса осуществлено в рамках проекта «Политический атлас мира» МГИМО (У) МИД РФ. С проектом можно ознакомиться по ссылке http://www.mgimo.ru/politatlas/.

системы на два больших класса: демократические и недемократические (автократические, включающие тоталитарные и авторитарные режимы). На рис. 6.13 правая часть распределения (выделена пунктирным овалом) представляет страны с демократическим типом политической системы, левая (выделена сплошным овалом) — автократические.

Признаки неоднородности в эмпирическом распределении ставят вопрос о правомерности анализа всех исследуемых объектов как единой совокупности. Фактически, это вопрос о том, имеем ли мы одну случайную величину — «институциональные основы демократии в странах мира», или более корректно разбить совокупность стран на две самостоятельные группы — демократические и автократические страны — и анализировать их по отдельности, как две случайные величины. Однозначного ответа на такого рода вопрос нет; в каждом случае принимается во внимание степень выраженности признаков неоднородности, содержательная природа рассматриваемого признака, цель и задачи исследования. Но сам факт наличия элементов неоднородности всегда очень важен.

Второе типичное отклонение распределения от нормального закона — наличие выбросов. Выбросом в статистической науке называются нетипичные, резко выделяющиеся наблюдения, лежащие вне характерной для распределения тенденции. Для одномерных распределений речь идет об экстремально высоких или экстремально низких значениях переменной. Количественное определение выброса связано с рассмотренным нами ранее правилом трех сигм. В соответствии с ним, в интервал от -1 до 1 стандартного отклонения от среднего значения попадают 68,3% всех значений, в интервал ±2 стандартных отклонения — 95,4% всех значений и, наконец, в интервал ±3 стандартных отклонения от центра — 99,7% всех значений. Выбросом, таким образом, является наблюдение, удаленное от центра более чем на три стандартных отклонения. Впрочем, как правило, выбросы достаточно легко обнаружить визуально.

Так, на рис. 6.14 показано распределение электоральной поддержки партии «Яблоко» по регионам России на выборах депутатов Государственной Думы 2011 г.

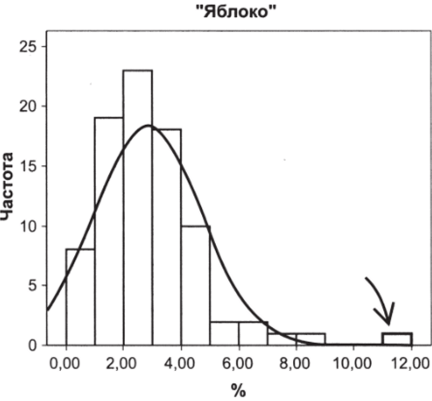
Рис. 6.14.

Стрелкой показан выброс, лежащий в стороне от основной совокупности (в остальном достаточно хорошо подчиняющейся нормальному закону). Это город Санкт-Петербург, где партию «Яблоко» поддержали примерно 11,6% проголосовавших. Средний процент поддержки этой партии по регионам составляет около 2,9%, стандартное отклонение равно 1,8%. Нетрудно посчитать, что питерский результат партии отстоит от ее среднего результата почти на пять стандартных отклонений.

Почему важны выбросы? Дело в том, что к их наличию чувствительны, с одной стороны, многие описательностатистические показатели, с другой — меры связи между показателями (их мы детально рассмотрим в следующих главах). В частности, на выбросы сильно реагирует средняя арифметическая. Так, дан следующий числовой ряд:

{1,2, 3, 4, 5, 6, 7, 8, 9}.

Нетрудно подсчитать среднюю арифметическую — она равна 5. Теперь изменим последнее значение с 9 на 99:

{1,2, 3, 4, 5, 6, 7, 8,99}.

Средняя изменилась радикальным образом: теперь она равна 15. Это число «повисает в пустоте» между основной массой наблюдений и единственным выбросом. Становится неясным, какую полезную информацию о совокупности в целом несет в себе это число. И любой выброс будет оказывать тот же эффект — «тянуть на себя» среднюю арифметическую.

При этом другая мера центральной тенденции — медиана — совершенно нечувствительна к выбросам. Такую нечувствительность к разного рода «перекосам» в распределениях в статистике часто называют робастностью. При замене 9 на 99, повлекшей такие драматические изменения средней арифметической, с медианой не происходит ничего. И для первого, и для второго ряда медиана составляет 5. При наличии выбросов медиана является лучшей оценкой центральной тенденции по сравнению со средним арифметическим.

Те же самые соображения справедливы для всех описательно-статистических показателей, включающих в себя расчет средней арифметической. К сожалению, это все названные выше параметрические показатели. Так, например, стандартное отклонение при замене 9 на 99 изменится с 2,7 до 31,6. Поэтому лучшей оценкой вариации при наличии выбросов будет межквартильный размах по сравнению с дисперсией, стандартным отклонением и коэффициентом вариации.

Почему тогда не отказаться вообще от среднего арифметического в пользу медианы? Дело в том, что параметрические оценки центра и разброса точнее, чем непараметрические, но при условии соответствия распределения нормальному закону. Непараметрические оценки являются более «грубыми», но при этом гораздо меньше зависят от распределения. Как всегда в статистическом анализе, бесплатного сыра не бывает: приобретая в точности, мы теряем в робастности, и наоборот.

Практическая рекомендация состоит в том, чтобы для параметрических переменных всегда рассчитывать и медиану, и среднюю арифметическую, а также оценивать различия между ними. Нормальное распределение как математическая модель характеризуется равенством медианы и средней: Me = р. Для эмпирических распределений строгого равенства не будет практически никогда, но можно оценить близость этих оценок. Чем сильнее медиана отличается от средней арифметической, тем сильнее отклонение эмпирического распределения от нормального закона.

Но вернемся к проблеме выбросов. Как только выбросы обнаружены, возникает еще один ответственный выбор: либо избавиться от сильно отклоняющихся значений (так называемая «чистка выбросов»), либо оставить их в анализируемой совокупности. Принятие такого решения должно предваряться не только оценкой того, насколько экстремален выброс, но и содержательным анализом причин сильного отклонения значения от центра совокупности. Так, в Санкт-Петербурге партия «Яблоко» устойчиво — из одного электорального цикла в другой — получает существенно больший процент голосов, чем в среднем по России. Это связано с особенностями электоральной культуры жителей Северной столицы, а также с наличием сильной региональной партийной организации. Таким образом, мы имеем дело с устойчивым и закономерным явлением, и это аргумент против удаления выброса.

Рассмотрим другой пример, теперь взяв в качестве эмпирического материала президентские выборы в России 2004 г. в разрезе субъектов Федерации. Рассмотрим распределение электоральной поддержки одного из кандидатов — Сергея Глазьева (см. рис. 6.15).

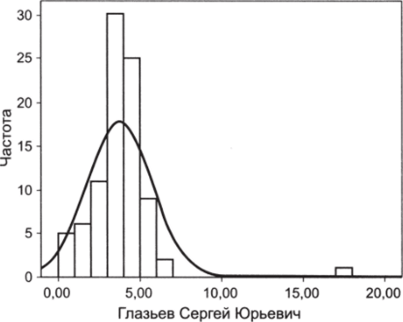
Рис. 6.15.

Бросается в глаза наличие одного наблюдения, в котором поддержка С. Глазьева приобретает нетипично большое значение — 17,2% (при средней =4%). Выбросом, причем очень сильным, в нашем примере является Красноярский край, и это имеет вполне определенное объяснение. Дело в том, что незадолго до президентских выборов 2004 г. С. Глазьев принимал участие в выборах губернатора данного региона и получил неплохой показатель поддержки, заняв третье место. Соответственно, в ходе губернаторской кампании он сформировал в крае локальную электоральную базу, существенно превышающую среднюю по России. Таким образом, появление выброса обусловлено действием специфического для региона фактора, а именно фактора локальной поддержки, сформированной в ходе региональной избирательной кампании. При этом данный фактор не является долговременным и систематически действующем, и это аргумент в пользу удаления выброса.

В любом случае, к операции удаления выбросов следует подходить очень сдержанно: в политической науке мы часто сталкиваемся с ситуациями, когда объектов измерения немного, и каждое наблюдение ценится «на вес золота». В то же время, если принимается решение о сохранении выброса, следует провести два вида анализа: с включением выброса и с его исключением, и сравнить полученные результаты.

Еще одним распространенным отклонением распределения от нормального является асимметрия. Симметричным является распределение, в котором частоты любых двух интервалов, равноотстоящих в обе стороны от центра распределения, равны (или приближенно равны) между собой. Можно выразить эту мысль и по-другому. Если мы мысленно «согнем» гистограмму распределения по линии среднего значения, левая и правая части колокола должны примерно совпасть. Если они существенно различаются, имеет место асимметричное распределение.

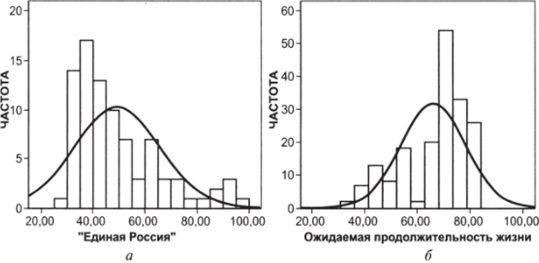
Различают правую и левую асимметрию. Так, на рис. 6.16а, где показано распределение поддержки партии «Единая Россия» по регионам на парламентских выборах 2011 г., имеется правая асимметрия. На рис. 6.166, на котором отображено распределение переменной «ожидаемая продолжительность жизни при рождении» (по странам мира), наблюдается левая асимметрия. Направление асимметрии определяется тем, в какую сторону направлен «хвост» распределения.

Степень асимметричности распределения можно оценить количественно. Для этой цели существует коэффициент асимметрии, рассчитываемый по формуле.

Рис. 6.16. а) Правая асимметрия; б) левая асимметрия.

Таким образом, коэффициент асимметрии представляет собой отношение суммы кубов отклонений наблюдений от среднего арифметического к произведению числа наблюдений на куб стандартного отклонения.

Практически же важно запомнить следующее. Коэффициент асимметрии может принимать как положительные, так и отрицательные значения. Первые свидетельствуют о правой асимметрии, вторые — о левой. При правой асимметрии медиана меньше среднего арифметического, при левой — больше.

Для теоретического нормального распределения А = 0, т. е. оно полностью симметрично. Чем сильнее отклонение от нуля (в любую сторону), тем сильнее выражена асимметрия. Эмпирически, асимметрия считается существенной при А > 10,5 |, сильной — при А > | 1 |. Так, распределение «Единой России» на рис. 6.16д обладает сильной правой асимметрией, так как А ~ 1,2. Распределение ожидаемой продолжительности жизни на рис. 6.165 обладает значительной левой асимметрией: А ~ -0,9.

Как и при других отклонениях от нормального распределения, наличие асимметрии должно быть поводом для постановки вопроса о ее содержательной природе. Рассмотрим в качестве примера изменения в распределении явки (электоральной активности) российских избирателей на федеральные выборы с 1991 по 2007 г. в разрезе регионов (см. рис. 6.17).

Основную тенденцию в изменении формы распределения можно охарактеризовать как переход от симметрии к правой асимметрии. Причем «переломным» в этом смысле является 2000 год, где впервые появляется небольшой правый «хвост», образуемый преимущественно национальными республиками. Фактически, правая асимметрия становится выраженной в период первых президентских сроков В. Путина и совпадает с эпохой «построения вертикали власти», когда явка на выборы в значительной мере становится функцией административной мобилизации. Однако население разных субъектов Федерации обладает разной степенью «проницаемости» по отношению к административному ресурсу. Последний (благодаря использованию клановых и клиентельных сетей) особенно силен именно в национальных республиках. Таким образом, простейший описательно-статистический анализ одномерных распределений позволяет оценить изменения, происходящие в «большой политике».

Что делать с асимметричными распределениями? Очевидно, удаление отдельных наблюдений здесь ни к чему не приведет. Одним из практических способов «выпрямления» распределений с сильной асимметрией является логарифмическое преобразование. Оно заключается в замене исходных значений их логарифмами, как правило — натуральными^[1]. Логарифмирование бывает очень эффективным в тех случаях, когда асимметрия является правой. При левой асимметрии можно сначала пересчитать переменную в величи;

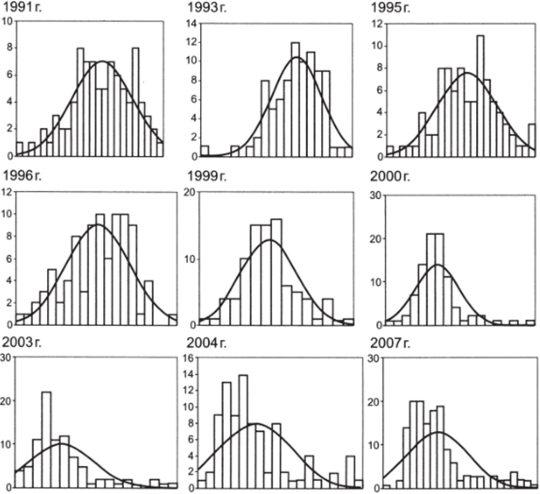
Рис. 6.П

ну, обратную ей, чтобы получить зеркальное отображение распределения с изменением знака асимметрии. Например, переменная X — «% населения за чертой бедности» — может быть преобразована в величину «% населения над чертой бедности» с помощью простейшей линейной операции 100% - X

В целом распределение случайной величины, логарифм которой обладает нормальным распределением, называется логнормальным (lognormal). Это весьма распространенный в политических исследованиях класс распределений. Следует учесть, что исходное эмпирическое распределение может быть совсем не похоже на нормальное. Например, такой значимый и широко используемый показатель, как ВВП на душу населения по странам мира, распределен следующим образом (см. рис. 6.18).

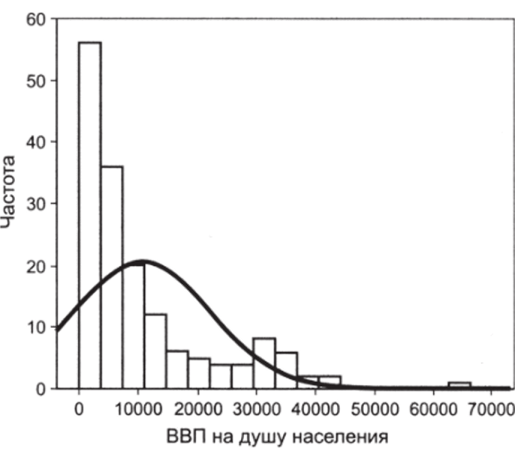
Рис. 6.18.

Это распределение кажется очень далеким от нормального. Оно обладает очень сильной асимметрией (Л = 1,6), плюс ко всему в правой части имеется выброс! Однако картина радикально меняется после логарифмирования (см. рис. 6.19).

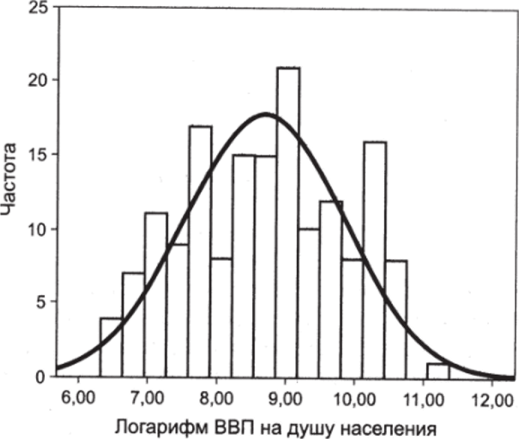
Рис. 6.19.

Теперь мы наблюдаем хорошее приближение к нормальному закону.

Логарифмическое преобразование легко выполняется в программе Excel. Для его отработки выполним следующее упражнение.

Упражнение 6.5

Вернемся к данным предыдущего упражнения — итогам президентских выборов 2008 г. в США. Будем работать с поддержкой Б. Обамы.

1. Используя надстройку «Анализ данных — гистограмма», постройте графическое распределение переменной Obama. Получится следующее (см. рис. 6.20).

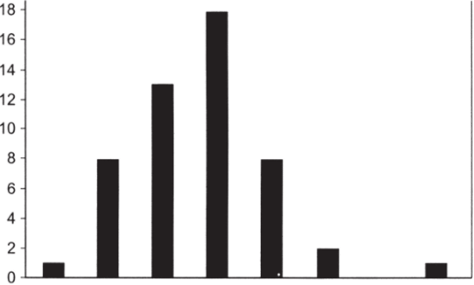
Рис. 6.20.

Распределение обладает правой асимметрией (коэффициент составляет примерно 0,9).

• 2. Прологарифмируем переменную Obama, используя функцию «=1п». Она возвращает натуральный логарифм числа. Удобнее всего посчитать логарифм для первого наблюдения, а затем «растянуть» функцию до конца столбца.
• 3. Построим гистограмму логарифмированной величины (см. рис. 6.22).

Различия между рис. 6.20 и рис. 6.22 не выглядят кардинальными, однако уменьшение асимметрии оказалось очень существенным: коэффициент сократился с 0,9 до 0,1. Последнее значение свидетельствует о том, что распределение практически симметрично.

Рис. 6.21.

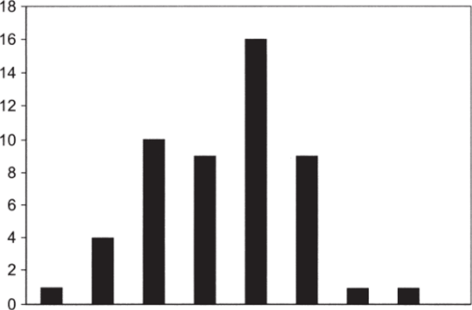
Рис. 6.22.

Наиболее радикальным средством выравнивания распределений является еще одно преобразование — ранговое. Оно представляет собой замену значений исходной параметрической переменной рангами — порядковыми номерами наблюдений в ранжированном ряду. Рассмотрим технику рангового преобразования, выполнив.

Упражнение 6.6

Возьмем данные о числе жертв терактов (ЖТА), совершенных в стране в течение года (2006 г.; см. табл. 6.7). Чтобы не загромождать таблицу, оставим только те страны, где это число существенно отличается от нуля (к счастью, таких стран не так уж много). Таблица в электронном виде доступна по ссылке http://polit.msu.ru/kaf/lab_quant/.

Таблица 6.7.

• 1. Ранжируйте страны по числу жертв терактов, используя опцию «Сортировка». В данном случае принципиально, чтобы ранжирование происходило по возрастанию. Это вытекает из основ теории измерений, — увеличению числа жертв терактов должно соответствовать увеличение значений переменной, которая возникнет в результате рангового преобразования.
• 2. Присвойте каждой стране номер от 1 до 25.

Здесь, однако, возникает одна проблема. Число жертв террористических актов в двух странах — Алжире и Мьянме — совпадает. Мы не имеем права (вновь в соответствии с теорией измерений) присвоить им разные ранги. Выход из положения см. в п. 3.

3. Для объектов с одинаковыми значениями посчитайте среднее арифметическое порядковых номеров и присвойте получившиеся числа каждому из объектов. Так, в нашем случае (табл. 6.8) Алжир и Мьянма имеют порядковые номера 7 и 8. Их среднее составляет 7,5. Именно такой ранг присваивается этим двум странам.

В результате рангового преобразования мы получаем порядковую переменную особого рода. Если построить гистограмму ее распределения, она почти всегда будет очень похожа на гистограмму равномерного распределения. Мы говорим «похожа», потому что к порядковым переменным понятие закона распределения неприложимо. Для нашего случая см. рис. 6.23.

При таком распределении принципиально не может возникать, к примеру, проблем с выбросами. Однако и цену за отсутствие подобных проблем приходится платить очень высокую: уходя от параметрических шкал, мы теряем всю информацию о расстояниях между наблюдениями. Так, после рангового преобразования Ирак и Индию разделяет единица, — так же как и другие соседние объекты. В исходном измерении Ирак опережает Индию почти в 16 раз!

В заключение этой главы еще раз отметим главное. Описательная статистика — это первый шаг в любом анализе данных. При всей своей простоте (на самом деле, весьма относительной), она способна дать очень многое как в пла;

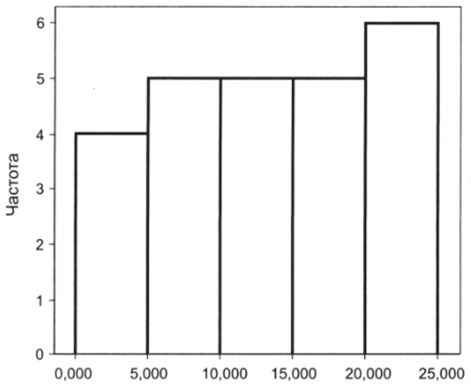
Рис. 6.23.

не содержательного понимания исследуемых данных, так и в плане выработки оптимальной стратегии их дальнейшего анализа.

Ьродскии Я.С. Статистика. Вероятность. Комбинаторика. М., 2008. С. 17−118.

Доннелли Р. Статистика. М., 2006. С. 28−77.

Иванов О.В. Статистика. Учебный курс для социологов и менеджеров. М., 2005. Ч. 1. С. 26−70.

Мангейм Дж., Рич Р. Политология. Методы исследования. М., 1997. С. 356−407.

Gill J. Essential Mathematics for Political and Social Research. Cambridge; N.Y., 2006. P. 361−367.

Интернет-ресурсы

Clayton State University, School of business. Electronic Textbook on Business Statistics:

http://business.clayton.edu/arjomand/book/sbk07.htm

http://business.clayton.edu/arjomand/book/sbk08.htm

• [1] Напомним, что основанием натуральных логарифмов является числое =2,71 828… .