Оценка параметров линейной регрессии

Следующий вопрос состоит в том, как получить состоятельную, несмещенную и эффективную — «хорошую» оценку регрессионной модели. Нужно получить такие оценки Ь₀ и Ь_{, чтобы линия регрессии, которую задают эти параметры, наилучшим образом соответствовала имеющимся данным. Например, на рис. 10.8 мы видим, что линия 2 адекватно отражает тенденцию в совместном распределении X и Y, а линия 1 — нет.

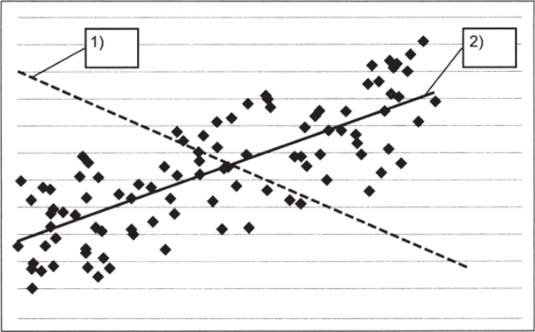
Рис. 10.8.

Очевидно, однако, что оценки «на глаз» явно недостаточно; требуется какой-то формальный критерий соответствия модели реальным данным. Введем еще одно очень важное для регрессии понятие — понятие остатка. Остаток — это разность между реальным, наблюдаемым значением зависимой переменной и предсказанным моделью значением:

Можно также сказать, что остаток является реализацией случайной ошибки для каждого конкретного наблюдения.

Все предсказанные значения Y лежат на линии регрессии; реальные же значения У, разбросаны вокруг нее. Таким образом, в каждом случае существует некоторое расстояние между реальностью и предсказанием. Это расстояние рассчитывается, естественно, по оси О У, для разных наблюдений оно может быть значительным или практически несущественным, положительным или отрицательным (рис. 10.9).

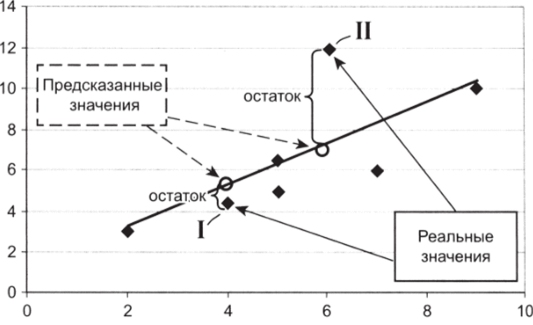
Рис. 10.9.

Итак, для каждого /'-го объекта мы имеем значение остатка. Для наблюдения I на рис. 10.9 предсказанное значение выше по сравнению с реальным; соответственно, значение остатка будет отрицательным. Для наблюдения II модель, напротив, дает заниженное предсказание, и значение остатка будет положительным. Остаток — это мера того, насколько линейная модель «ошибается» в каждом конкретном случае. Требуется получить какое-то одно число, характеризующее «общую ошибку» модели. Складывать остатки бессмысленно, поскольку отрицательные и положительные значения («завышения и занижения») компенсируют друг друга и, в результате, сумма будет нулевой. Правильный подход состоит в том, чтобы суммировать квадраты остатков', возведение в квадрат избавляет нас от отрицательных значений. Сумму квадратов остатков мы будем иногда обозначать английской аббревиатурой RSS (Residual Sum of Squares), так как она активно используется в различных программных приложениях.

Итак, мы вплотную приблизились к формальному критерию оценки качества регрессионной модели, ее соответствия реальным данным. Наилучшими являются такие оценки параметров Ь₀ и Л, при которых сумма квадратов остатков минимальна. Иначе говоря, надо подобрать значения параметров, обеспечивающие минимальную совокупную ошибку модели:

Это правило лежит в основе одного из наиболее простых и, в то же время, действенных методов оценки параметров регрессионных моделей, который получил название метода наименьших квадратов (OLS, Ordinary Least Squares).

Рассмотрим, как «работает» этот метод, на самом простом примере. Пусть имеются всего два случая: в одном из них Y — 3 при Х= 1, во втором — У= 4 при Х= 2 (рис. 10.10).

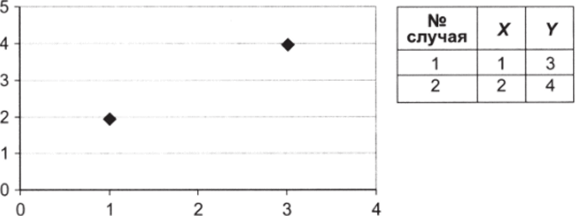
Рис. 10.10.

Предположим, что истинная модель связи между X v Y линейна и имеет вид.

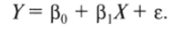
Данное утверждение может показаться формальным и излишним, но на самом деле это не так. В анализе связей необходимо на самой первой стадии исследования явным образом сформулировать предположение об «истинной» модели зависимости между показателями.

Оценим коэффициенты Ь₀ и 6, уравнения:

Из курса школьной математики нам известно, что через две точки можно провести прямую, причем только одну. На языке регрессионного анализа это означает, что модель не будет содержать случайной составляющей; ее предсказание будет совершенно точным, остатки будут равны нулю. Этот пример мы рассматриваем исключительно для того, чтобы понять внутреннюю «механику» метода наименьших квадратов.

В первом наблюдении X = 1. Предсказанное значение Y — Ь₀ + 6, х 1= Y = Ь_а + />, (по формуле 10.12). Остаток е, для первого наблюдения составляет е, = К, — К, = 3 — (6″ + + Ь_х) = 3 — Ь₀ — by Напоминаем, что 3 — наблюдаемое значение Y в первом случае.

Во втором случае Х= 2. Следовательно, Y = Ь₀ + А, х2 = Ь₀ + + 2/>|. Остаток е₂ = У₂ — Y₂ = 4 — (b₀ + 2b_t) = 4 — 26, — b₀.

Сумма квадратов остатков.

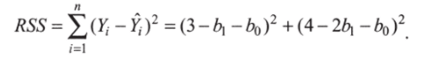
Преобразуем это выражение, используя школьную формулу (о — b — с)² = а² + Ь² + с² — lab — lac + 2 bc

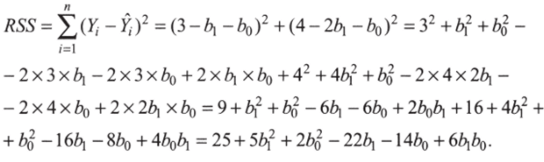
Теперь необходимо найти такие Ь₀ и by чтобы сумма квадратов остатков была минимальной. Это задача на поиск экстремума; соответственно, производная RSS должна быть приравнена к нулю. У нас два параметра, поэтому будем дифференцировать RSS одновременно по Ь₀ и по by

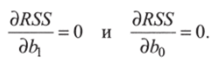
Возьмем частные производные:

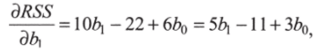
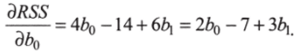
Решим систему уравнений:

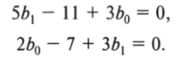
В результате получим Ь₀ = 2, 6, = 1. Оцененная модель имеет вид У = 2 + X/.

Как мы уже отмечали, ключевой параметр в нашей модели — р, геометрически являющийся угловым коэффициентом прямой. Знак коэффициента регулирует направление связи, величина р, — силу связи. Рассмотрим механизм этого влияния более детально, включив в анализ уже знакомые понятия — дисперсии (стандартного отклонения) и корреляции.