Алгоритм шифрования DES

Общая схема алгоритма. Алгоритм шифрования DES (Data Encryption Standard) был опубликован в 1977 г. и предназначался для защиты важной, но несекретной информации в государственных и коммерческих организациях США. DES основан на схеме Фейстеля. Реализованные в DES идеи были во многом позаимствованы в более ранней разработке корпорации IBM — шифре «Люцифер» (в IBM работал X. Фейстель, автор одноименной схемы). Но для своего времени «Люцифер» был слишком сложным, и его реализации отличались низким быстродействием.

Алгоритм DES допускает эффективную аппаратную и программную реализацию, причем возможно достижение скоростей шифрования до нескольких мегабайт в секунду. Шифр DES блочный — преобразования в нем проводятся блоками по 64 бита. Ключ — 56-битный. Могут использоваться 64-битные ключи, но значащими являются только 56 бит — каждый восьмой разряд предназначен для контроля четности (шифр разрабатывался тогда, когда аппаратура была не слишком надежной и подобные проверки были необходимы). 56 бит — это восемь семибитовых ASCII символов, т. е. ключ (пароль) не может быть больше восьми букв. Если вдобавок использовать только буквы и цифры, то количество возможных вариантов будет существенно меньше максимально возможного числа 2^j6.

Шифрование производится в 16 раундов. В каждом раунде к тексту применяются единичные комбинации простых криптографических преобразований: замена, а затем — перестановка, зависящая от ключа.

После первоначальной перестановки (IP) блок разбивается на правую (R) и левую (L) половины длиной по 32 бита. Затем выполняется 16 раундов преобразований F, в которых данные объединяются с ключом. После 16-го раунда правая и левая половины объединяются, и алгоритм завершается последней перестановкой 1Р~обратной по отношению к первоначальной (рис. 2.6).

После заключительного раунда DES левая и правая половины не меняются местами, вместо этого объединенный блок 7?₁₆L₁₆ используется как вход заключительной перестановки IP ^!. В этом нет ничего особенного, перестановка половинок с последующим циклическим сдвигом привела бы к такому же результату. Это сделано для того, чтобы алгоритм имел сходную структуру как для шифрования, так и для дешифрирования.

Начальная перестановка IP (Initial Permutation) задается табл. 2.1.

Биты входных данных нумеруются по порядку, начиная с единицы. Таблица трактуется следующим образом: значение 58-го бита входной последовательности перемещается в битовую позицию 1, бит 50 — в битовую позицию 2, бит 42 — в битовую позицию 3 и т. д.

Конечная перестановка — IP~¹ — является обратной по отношению к начальной IP и задается табл. 2.2.

Таблицы, задающие все перестановки и замены, жестко определены стандартом.

Начальная перестановка IP и соответствующая заключительная перестановка IP ¹ не влияют на безопасность DES. Эта перестановка в первую очередь служила для облегчения побайтной загрузки данных открытого текста и шифротекста в микросхему DES (поскольку DES появился рань;

Рис. 2.6. Общая схема алгоритма DES.

Таблица 2.1

Начальная перестановка IP

Таблица 2.2

Конечная перестановка IP ¹

ше 16- и 32-битовых микропроцессорных шин). Поскольку программная реализация этой многобитовой перестановки нелегка (в отличие от тривиальной аппаратной), во многих программных реализациях начальная и заключительные перестановки не используются. Хотя такой новый алгоритм не менее безопасен, чем DES, он не соответствует стандарту и поэтому не может называться DES.

На каждом этапе биты ключа сдвигаются, и затем из 56 битов ключа выбираются 48 битов с помощью перестановки со сжатием (PC). Правая половина входных данных увеличивается до 48 битов с помощью перестановки с расширением (Е или ЕР), а затем объединяется посредством XOR с 48 битами смещенного и переставленного ключа, проходит через восемь 5-блоков, образуя 32 новых бита, и переставляется снова (Р). Эти четыре операции выполняются функцией раундового преобразования Е (рис. 2.7). Затем результат функции F объединяется с левой половиной с помощью XOR. В итоге этих действий появляется новая правая половина, а затем левая и правая половины переставляются местами.

Рис. 2.7. Схема раундового преобразования шифра DES.

Если В, — это выходные данные (результат) /-го раунда, L_i и В, — левая и правая половины B_j} K_t — 48-битовый раундовый ключ, a F — раундовое преобразование, выполняющее все подстановки, перестановки и побитовое XOR с ключом, то /-й раунд DES (рис. 2.8) может быть описан как.

Рассмотрим подробнее операции, производимые в каждом из раундов алгоритма DES.

Перестановка с расширением. Перестановка с расширением Е (или ЕР, Expansion Peimutation) расширяет 32-битный правый полублок входного текста до 48 бит. Е производит дублирование и перестановку некоторых элементов блока. Эта функция решает две задачи:

• • приводит размер правой половины в соответствие с длиной ключа для последующего их сложения с помощью операции XOR;
• • обеспечивает влияние одного входного бита на две таблицы замен вместо одной, что ускоряет рост зависимости битов результата (шифротекста) от каждого из битов исходных данных. Это называется лавинным эффектом.

Рис. 2.8. Раунд шифрования DES

Алгоритм DES спроектирован так, чтобы как можно быстрее добиться зависимости каждого бита шифротекста от каждого бита открытого текста и каждого бита ключа.

Перестановка с расширением приведена на рис. 2.9 и задается табл. 2.3.

Рис. 2.9. Схема перестановки с расширением.

Таблица 2.3

Перестановка с расширением Е

Хотя выходной блок больше входного, перестановка с расширением Е генерирует для каждого входного блока уникальный выходной блок. После расширения полученный 48-разрядный блок складывается побитно по модулю 2 (XOR) с раундовым ключом X, схема генерации которого будет рассмотрена ниже.

Подстановка с помощью S-блоков. 48-битовый результат сложения расширения правого блока и раундового ключа разбивается на восемь фрагментов, но шесть бит, которые подаются на входы соответствующих таблиц замен (S-блоков). У каждого S-блока 6-битовый вход и 4-битовый выход (рис. 2.10), всего используется восемь различных S-блоков.

Рис. 2.10. Блок замены DES

Таблицы замен являются фиксированными и содержат четыре строки, но 16 значений от 0 до 15 (4-битовые числа). Строки и столбцы таблиц замены нумеруются, начиная с нуля (табл. 2.4).

Таблица 2.4

S-блоки алгоритма DES

Каждый отдельный 6-битовый подблок обрабатывается отдельным S-блоком следующим образом и определяет, под какими номерами столбцов и строк искать выходное значение. Пусть на вход подстановки подается 6-разрядный блок В = Ь_ХЬ₂.Ь^. Тогда совокупность старшего и младшего разрядов Ьф₆ (число от 0 до 3) будет указывать номер строки, а четырехбитное значение Ь._}Ь₃Ь_ЛЬ₅ (число от 0 до 15) — номер столбца. Ячейка на пересечении найденных строки и столбца определяет выходное значение подстановки.

Пример 2.5.

Пусть на вход шестого S-блока (т.с. биты с 31 по 36 результата ХОК) попадает 110 011 (рис. 2.11). Первый и последний биты, объединяясь, образуют 11₂ = 3, что соответствует 3-й строке S₆. Средние четыре бита образуют 1001₂ ⁼ 9, что соответствует 9-му столбцу S₆. Элемент S₆, находящийся па пересечении 3-й строки и 9-го столбца, — это 14 = 1110₂. Выход S₆ — битовая строка 1110 (вместо 110 011 подставляется 1110).

Рис. 2.11. Пример действия S-блоков (S₆).

Подстановка с помощью S-блоков является ключевым этапом DES. Sблоки нелинейны, и именно они в большей степени, чем все остальное, обеспечивают безопасность DES.

На последнем шаге 4-битные значения, полученные после выполнения замен, объединяются в 32-битное число, после чего над ним выполняется преобразование Р, представляющее собой простую перестановку (табл. 2.5).

Таблица 2.5

Перестановка Р

Поскольку DES построен на схеме Фейстеля, результат перестановки с помощью P-блока объединяется посредством XOR с левой половиной первоначального 64-битового блока. Затем левая и правая половины меняются местами, и начинается следующий раунд. После последнего раунда DES левая и правая половины местами не меняются.

Расшифрование DES проводится абсолютно так же, как и шифрование, однако с обратным порядком использования раундовых ключей. В i-м раунде расшифровки используется ключ K_xl__t.

Процедура расширения ключа. Схема процедуры расширения ключа алгоритма DES приведена на рис. 2.12 (символом «< обозначена операция циклического сдвига влево).

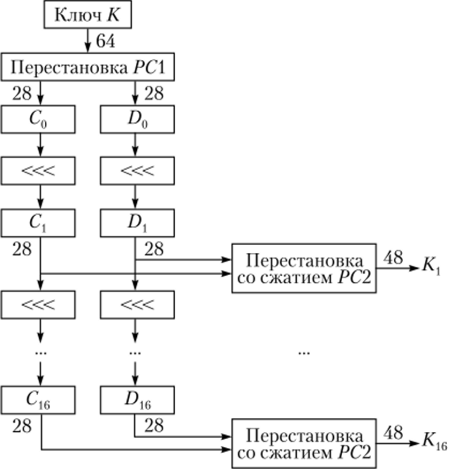
Рис. 2.12. Вычисление раундовых ключей Как было отмечено ранее, секретный ключ шифра DES имеет длину 64 бита, но каждый восьмой предназначается лишь для контроля четности, поэтому эффективная длина ключа — 56 бит. Функция PC 1 (Permuted Choice — выбор с перестановкой) осуществляет перестановку элементов исходного блока, отбрасывая биты четности (8-й, 16-й и т. д. биты). Начальное преобразование ключа определяется таблицей перестановки (табл. 2.6).

После перестановки полученный блок делится на полублоки С₀ и D₀ длиной 28 бит каждый. В зависимости от номера раунда полублоки C_t и D_tнезависимо друг от друга преобразуются путем циклического сдвига влево на одну или две позиции (табл. 2.7).

После сдвига половины ключа объединяются, а затем выбирается 48 из 56 битов. Поскольку при этом не только выбирается подмножество битов,.

Таблица 2.6

Перестановка PCi процедуры расширения ключа.

Таблица 2.7

Величина циклического сдвига влево.

но и изменяется их порядок, эта операция называется перестановкой со сжатием (РС2). Ее результатом является набор из 48-битовых раундовых ключей. Перестановка со сжатием определяется табл. 2.8.

Таблица 2.8

Перестановка со сжатием РС2

Сочетание циклического сдвига и сжимающей перестановки приводит к тому, что в каждом раундовом ключе используется уникальный набор битов исходного ключа шифрования. Каждый бит используется приблизительно в 14 из 16 подключей, хотя не все биты используются в точности одинаковое число раз.

При расшифровке можно применять ту же процедуру расширения ключа, но использовать раундовые ключи в обратном порядке. Существует и другой вариант — в каждом раунде процедуры расширения ключа вместо циклического сдвига влево выполняется циклический сдвиг вправо (табл. 2.9).

Таблица 2.9

Величина циклического сдвига вправо при генерации ключей расшифрования.

Такой подход сразу даст нужные для расшифровки ключи раундов. Возможность выполнения расширения ключа «на лету» (особенно, если эта возможность существует как для шифрования, так и для расшифровки) считается достоинством алгоритма шифрования, поскольку в этом случае:

• • расширение ключа можно выполнять параллельно шифрованию (расшифровке) — экономится время;
• • нет необходимости хранить ключи других раундов, кроме текущего — экономится память.

Безопасность DES. Шифр DES является наиболее изученным — с самого начала его использования криптоаналитики со всего мира прилагали массу усилий по его взлому. Фактически DES дал развитие многим новым направлениям криптоанализа, таким как линейный, дифференциальный криптоанализ, криптоанализ на связанных ключах.

Все предложенные варианты криптоанализа полноценного (полнораундового немодифицированного) DES оказались лишь ненамного эффективнее метода «грубой силы». К тому же они требовали огромного количества пар «открытый текст — шифротекст», получение которых на практике весьма затруднено.

Некоторое время шифр DES считался достаточно безопасным. Однако по мере развития вычислительной техники короткий 56-битный ключ привел к тому, что атака путем полного перебора ключевого множества стала относительно легко реализуемой. Кроме того, сразу после появления DES были обнаружены слабые ключи.

Слабые ключи. Из-за того что первоначальный ключ изменяется при получении подключа для каждого этапа алгоритма, определенные первоначальные ключи являются слабыми. Первоначальное значение расщепляется на две половины, каждая из которых сдвигается независимо. Если все биты каждой половины равны нулю или единице, то для всех этапов алгоритма используется один и тот же ключ. Это может произойти, если ключ состоит из одних единиц, из одних нулей или если одна половина ключа состоит из одних единиц, а другая — из одних нулей. Кроме того, два слабых ключа обладают другими свойствами, снижающими их безопасность.

Четыре слабых ключа показаны в шестнадцатеричном виде в табл. 2.10 (каждый восьмой бит — это бит четности).

Таблица 2.10

Слабые ключи DES.

Кроме того, некоторые пары ключей при шифровании переводят открытый текст в идентичный шифротекст. Иными словами, один из ключей пары может расшифровать сообщения, зашифрованные другим ключом пары. Это происходит из-за метода, используемого DES для генерации подключей, — вместо 16 различных подключей эти ключи генерируют только два различных подключа. В алгоритме каждый из этих подключей используется восемь раз. Такие ключи, называемые полуслабыми ключами, в шестнадцатеричном виде приведены в табл. 2.11.

Ряд ключей генерирует только четыре подключа, каждый из которых четыре раза используется в алгоритме. Эти возможно слабые ключи перечислены в табл. 2.12.

Использование слабых ключей делает возможным применение метода криптоанализа, называемого слайдовой атакой. 64 слабых ключа — малая часть полного набора возможных ключей. Если ключ выбирается случайно,.

Таблица 2.11

Полу слабые пары ключей DES.

Таблица 2.12

Возможно слабые ключи DES.

вероятность выбрать одни из слабых ключей пренебрежимо мала. Кроме того, можно всегда проверять сгенерированный ключ на слабость.

Других слабых ключей DES в процессе исследований найдено не было.

Ключи-дополнения. Выполним побитное дополнение ключа, заменяя все нули на единицы и все единицы — на нули. Теперь, если блок открытого текста зашифрован оригинальным ключом, то дополнение ключа при шифровании превратит дополнение блока открытого текста в дополнение блока шифротекста. Если х обозначает дополнение х, то верно следующее:

На каждом этапе после перестановки с расширением подключи подвергаются операции XOR с правой половиной. Прямым следствием этого факта и является приведенное свойство комплиментарное™.

Это означает, что при выполнении вскрытия DES с выбранным открытым текстом нужно проверять только половину возможных ключей: 2⁵⁵ вместо 2⁵⁶. Э. Бихам (Eli Biham) и Л. Шамир (Adi Shamir) показали, что существует вскрытие с известным открытым текстом, имеющее ту же сложность, для которого требуется не меньше известных открытых текстов.

Вопрос, является ли такое свойство слабостью, так как появление комплиментарных блоков открытого текста в большинстве сообщений крайне маловероятно, остается открытым.

Лавинный эффект DES. В блочных многораундовых шифрах лавинный эффект обычно достигается благодаря тому, что в каждом раунде изменение одного входного бита ведет к изменениям нескольких выходных. Чтобы проверить наличие хорошего лавинного эффекта в конкретном алгоритме, можно использовать несколько критериев.

Криптографический алгоритм удовлетворяет лавинному критерию, если при изменении одного бита входной последовательности изменяется в среднем половина выходных битов. Приведенный лавинный критерий оценивает лавинный эффект по открытому тексту, аналогичным образом может быть определен лавинный критерий для оценки лавинного эффекта по ключу (при изменении одного бита ключевой последовательности изменяется в среднем половина выходных битов).

Криптографический алгоритм удовлетворяет строгому лавинному критерию, если при изменении одного бита входной последовательности каждый бит выходной последовательности изменяется с вероятностью ½. Криптографический алгоритм удовлетворяет критерию независимости битов, если при изменении любого входного бита любые два выходных бита изменяются независимо.

Для практической оценки лавинного эффекта будем использовать первый из перечисленных критериев (лавинный критерий по тексту и, но ключу). Для этого используют понятие кодового расстояния. Кодовым расстоянием d (расстояние Хэмминга) двух битовых последовательностей называется количество бит, на которые последовательности отличаются.

В работе В. Столлингса^[1] приведены результаты лавинного эффекта по тексту (табл. 2.13) при шифровании алгоритмом DES двух 64-битовых последовательностей, различающихся между собой одним (первым) битом:

• 0 0 0 0 0 0 0 0 и
• 10 000 000 0 0 0 0 0 0 0

с ключом.

1 1 001 011 100 100 1 100 010 11 100 11 000 11 000 110 010;

и лавинного эффекта по ключу (табл. 2.14) при шифровании последовательности:

1 101 000 10 000 101 10 111 1 111 010 10 011 1 110 110 11 101 011 10 100 100.

с двумя различными ключами, различающимися лишь одним (первым) битом:

• 1 110 010 1 111 011 1 101 111 11 000 11 101 100 110 001 1 101 110 и
• 110 010 1 111 011 1 101 111 11 000 11 101 100 110 001 1 101 110.

Таблица 2.13

Лавинный эффект по тексту (DES)¹

Таблица 2.14

Лавинный эффект по ключу (DES)²

Таким образом, DES демонстрирует достаточно сильный лавинный эффект. При малых изменениях, как в открытом тексте, так и в ключе шифрования, наблюдаются различия более чем для половины битов, лавинный эффект оказывается явно заметным уже после нескольких раундов шифрования. Каждый бит выхода зависит от всех битов входа уже после пяти раундов, а после восьми раундов эта зависимость случайна.

Кодовое расстояние дает абсолютные величины — число несовпадающих бит. Однако у разных алгоритмов шифрования размер блоков входного и, соответственно, выходного текста может быть различным. Для возможности сравнения различных алгоритмов (вариантов алгоритма с разной длиной блока) следует использовать относительную величину X = d/N, где N — длина блока алгоритма.

При такой трактовке лавинного эффекта 0 < X < N, в графическом представлении X будет близким к ½. Данные табл. 2.13 и 2.14 для относительной величины X приведены на рис. 2.13.

Рис. 2.13. Лавинный эффект алгоритма DES (X).

Проектирование S-блоков DES. Лавинный эффект в большей степени достигается за счет использования S-блоков, поэтому их проектирование является крайне ответственной задачей. После появления публикаций о дифференциальном криптоанализе IBM раскрыла критерии проектиро-^[2][3]

вания S-блоков алгоритма DES. Критерии проектирования S-блоков следующие:

• • ни один выходной бит S-блока не должен быть слишком близок к линейной функции входных битов;
• • если зафиксировать крайние левый и правый биты S-блока, изменяя четыре средних бита, то каждый возможный 4-битовый результат получается только один раз;
• • если два входа S-блока различаются только одним битом, результаты должны различаться по крайней мере на два бита;
• • если два входа S-блока различаются только двумя центральными битами, результаты должны различаться, но крайней мере на два бита;
• • если два входа S-блока различаются двумя первыми битами, а их последние два бита совпадают, результаты не должны быть одинаковыми;
• • для любого ненулевого 6-битового различия между входами не более чем восемь из 32 пар входов могут приводить на выходе к одинаковому различию.

• [1] Столлингс В. Криптография и защита сетей: принципы и практика. М.: Издательскийдом «Вильямс», 2001.
• [2] Столлингс В. Криптография и защита сетей: принципы и практика.
• [3] Там же.