Шифр Шамира. 
Криптографические методы защиты информации

Шифр Шамира (Adi Shamir) был первым, позволяющим организовать обмен секретными сообщениями по незащищенной линии связи без обмена секретными ключами. Рассмотренная ранее система Диффи — Хеллмана позволяет сформировать только секретный ключ, а передача сообщения потребует использования некоторого шифра.

Шифр Шамира заключается в следующем. Пусть имеются два абонента, А и В, соединенные линией связи, и, А хочет передать секретное сообщение В. А выбирает большое простое число р и открыто передает его абоненту В. Затем, А случайно выбирает два числа х_{ и х₂, такие, что они являются обратными друг другу по модулю р — 1:

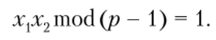
Числа х_х и х₂ являются личным ключом абонента, А он держит их в секрете и передавать не будет.

Абонент В также случайно выбирает два числа г/, и у₂, такие, что:

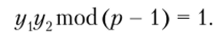
Числа у_{ и у₂ являются личным ключом абонента В и держатся в секрете.

Числам и у_{ выбираются абонентами случайно так, чтобы они были взаимно простыми с р — 1. Причем *, и г/, следует искать только среди нечетных чисел, так как р — 1 — четно. Числа х₂ и у₂ вычисляются с помощью расширенного алгоритма Евклида.

Теперь абонент, А может передать свое сообщение М, используя трехступенчатый протокол. Сообщение М рассматривается как число. Если М < р, то М передается сразу; если же М > р, то перед отправкой сообщение представляется в виде последовательности m_v m_v …, т₍, где все т. < р. Сообщения m_jf i = 1, t передаются последовательно, при этом для шифрования каждого m_i рекомендуется случайно выбирать новые пары ключей х_х и х₂, г/, и у₂; в противном случае надежность криптосистемы снижается. Таким образом, не умаляя общности, можно рассмотреть только случай М < р:

• 1) А вычисляет число X, = M^v> mod р, где М — исходное сообщение, и пересылает X, абоненту В;
• 2) В, получив X, вычисляет число У, = Xf¹ mod р и передает У, абоненту А,
• 3) А вычисляет число Х₂ = У*² mod р и передает его В;
• 4) В, получив Х₂, вычисляет число У₂ = Х₂² mod р, У₂ и есть исходное сообщение М.

Покажем, что У₂ = М. Заметим, что на основании теоремы Ферма для любого целого е > 0 выполняется: x^modp = x^{k (j)}~^i)+r modp = (l***)modp = _{= x}^.nod (^-i)_mocj p_{? где} r = emod (p — 1). Тогда.

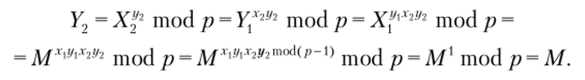
Значения X_vX₂n У, могут передаваться по открытому каналу, поскольку получение на их основе значений секретных ключей x_v х₂ и г/, практически невозможно (утверждение базируется на вычислительной сложности задачи дискретного логарифмирования при больших значениях р).

Никто другой, кроме абонента В, не сможет вычислить значения М, так как в вычислениях используются секретные ключи абонента В.

Пример 3.21.

Пусть Л хочет передать В сообщение М = 10. Л выбирает простое р = 23, х_х = 7 — взаимно простое с р — 1 = 22 (НОД (7, 22) = 1) и с помощью расширенного алгоритма Евклида вычисляет^ = х_х ¹ mod (р - 1) = 7 ¹ mod 22 = 19. Аналогично В выбирает параметры гу, = 5 — взаимно простое с 22 (НОД (5, 22) = 1) и вычисляет у₂ = г/,^-1 mod (р — 1) = 9. Протокол Шамира:

• 1) А —? В: X, = М^хЛ mod р = 10⁷ mod 23 = 14;
• 2) В — А: У, = Х^уХ mod р = 14⁵ mod 23 = 154;
• 3) А — В: Х₂ = Y* mod р = 15¹⁹ mod 23 = 19;
• 4) В проводит расшифрование: У₂ = X^yl mod р = 19⁹ mod 23 = 10 = М.

Шифр Шамира может быть легко обобщен на произвольное число абонентов.

Основным недостатком шифра является необходимость многоступенчатого обмена данными между абонентами, что в ряде случаев может оказаться весьма неудобным.