Методы определения поверхностного натяжения жидкостей и удельной свободной поверхностной энергии твердых тел

Основная характеристика свойств поверхности раздела фаз — удельная свободная поверхностная энергия и численно равная ей величина поверхностного натяжения, а — может быть сравнительно легко и с большой точностью определена для легкоподвижных границ раздела фаз жидкость — газ и жидкость — жидкость. Существует большое число детально разработанных методов определения по;

• 5^е
• 63

верхностного натяжения [14]Остановимся лишь на общих принципах основных методов измерения поверхностного натяжения жидкостей.

Методы измерения поверхностного натяжения жидкостей делят на статические, полустатические и динамические.

Статические методы основаны на изучении устойчивого равновесного состояния, к которому самопроизвольно приходит изучаемая система. Это позволяет получать истинно равновесные значения поверхностного натяжения, что очень важно при изучении растворов, особенно растворов высокомолекулярных соединений, для которых характерно длительное установление равновесного состояния поверхностных слоев. К числу статических относятся методы капиллярного поднятия, лежащей и висящей капли (пузырька), вращающейся капли, уравновешивания пластинки и др.

Метод капиллярного поднятия в его простейшем варианте основан на формуле Жюрена (1.21). При этом применяют тонкие капилляры, что обеспечивает сферичность поверхности мениска; использование же капилляров, хорошо смачиваемых жидкостью (0 = 0°), позволяет избежать трудностей, связанных с определением краевого угла.

При более точных измерениях необходимо учитывать поправку на объем жидкости над нижним уровнем мениска; при сферической форме мениска эта поправка равна разности объема цилиндра с высотой, равной радиусу основания, и полусферы того же радиуса, т. е.

тг* ~яг³ =1 лг³.При очень точных измерениях учитывают отклонение формы мениска от сферической (особенно, когда применяются широкие капилляры). С этой целью используют результаты численного интегрирования дифференциального уравнения Лапласа, которые приводятся в таблицах. Метод капиллярного поднятия может давать точность определения поверхностного натяжения до десятых и сотых долей мН/м.

В противоположность методу капиллярного поднятия группа методов, основных на изучении формы капель и пузырьков в поле силы тяжести, принципиально включает учет отклонения их формы от сферической, т. е. требует интегрирования уравнения Лапласа. При измерении поверхностного натяжения эти-^[1]

ми методами обычно находят какие-либо характерные геометрические параметры, показывающие степень отклонения поверхности от сферической (например, для капли, изображенной на рис. 1−27, ее максимальную ширину ^ и расстояние Н* от вершины до максимального сечения d_mах). Сопоставляя результаты измерений с табулированными значениями этих параметров, полученными численным интегрированием уравнения Лапласа, находят величину поверхностного натяжения а. Эта группа методов особенно ценна для определения поверхностного натяжения жидкостей при высокой температуре. Для этого капли фотографируют с помощью длиннофокусных оптических систем либо в рентгеновских лучах.

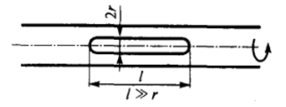
Рис. 1−31. Равновесная форма вращающейся капли.

Метод вращающейся капли позволяет измерять очень низкие значения межфазного натяжения на границах двух жидкостей. В этом методе трубка, заполненная жидкостью, приводится во вращение вокруг своей оси (рис. 1−31). В трубку вводится капля другой жидкости с меньшей плотностью. За счет действия центробежных сил эта менее плотная жидкость стремится расположиться ближе к оси вращения и, не касаясь стенок, вытягивается в тонкий столбик. Измеряя размеры столбика и скорость вращения со, можно при известной разности плотностей жидкостей (pi — Р2) определить поверхностное натяжение о межфазной поверхности. В первом приближении (при аппроксимации столбика цилиндром с радиусом г) имеем:

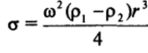
Несколько особняком среди других статических методов определения поверхностного натяжения находится удобный и точный метод уравновешивания пластинки (метод Вильгельм и). В этом методе закрепленную на коромысле весов тонкую пластинку шириной d, как правило, хорошо смачиваемую исследуемой жидкостью, погружают в жидкость. На поверхности пластинки с обеих ее сторон образуются мениски (рис. 1−32). Форма их поверхности и максимальная высота поднятия жидкости определяются уравнением Лапласа. Суммарный вес поднятой жидкости, приходящийся на единицу длины периметра пластинки, не зависит от.

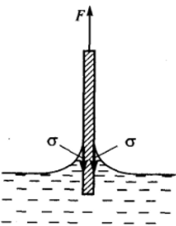
Рис. 1−32. Условия равновесия при измерении поверхностного натяжения по методу Вильгельми.

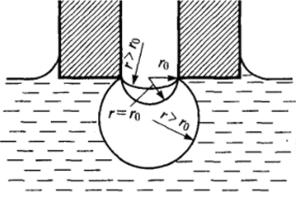
Рис. 1−33. Изменение радиуса кривизны поверхности пузырька при измерении поверхностного натяжения по методу максимального давления.

формы мениска и при нулевом краевом угле смачивания равен поверхностному натяжению о. Поэтому сила F которую необходимо приложить для уравновешивания пластинки, равна произведению поверхностного натяжения жидкости на удвоенную ширину пластинки, соответственно поверхностное натяжение определяется из условия, а = F/(2d) (при достаточно малой толщине пластинки). Этот метод в принципе не требует учета каких-либо поправок на форму мениска.

Полу статические методы определения поверхностного натяжения, как и статические, основаны на достижении системой некоторого равновесного состояния, но для полустатических методов это равновесие неустойчиво. Определение поверхностного натяжения основано здесь на изучении условий, при которых система теряет свое равновесие.

Так как приближение к границе устойчивости системы можно производить очень медленно, полустатические методы позволяют получать значения поверхностного натяжения, весьма близкие к равновесным. Однако при исследовании каждой новой системы необходим подбор оптимальной скорости приближения к равновесному состоянию, чтобы измерения не были чрезмерно длительными и вместе с тем обеспечивали получение близких к истинно равновесным результатов. Среди полустатических методов наиболее употребительны метод наибольшего давления, необходимого для образования в жидкости пузырька (или капли другой жидкости), метод отрыва кольца от поверхности жидкости и методы взвешивания и счета капель (сталагмометрия).

Вметоде наибольшего давления под действием приложенного извне избыточного давления Ар через калиброванный капилляр (рис. 1−33) в объем жидкости продавливается пузырек газа или капля другой жидкости. По мере роста пузырька радиус кривизны его поверхности /-уменьшается и достигает минимального значения, равного радиусу капилляра когда поверхность пузырька приобретает форму полусферы. При дальнейшем увеличении объема пузырька радиус кривизны его поверхности возрастает (г > /*>). Следовательно, капиллярное давление р_а = 2а/г при г = по достигает своего максимального значения, равного 2ст//&. Соответственно при Ар < 2о/го система механически устойчива; при Ар > 2а//*> капиллярное давление не может уравновесить приложенного давления Ар: пузырек теряет свою устойчивость и, быстро разрастаясь, отрывается от поверхности. При этом обычно происходит заметный спад разности давлений в капилляре и внешней жидкости Ар, что позволяет четко фиксировать максимальное значение перепада давления, отвечающего условию Артах ⁼ 2с/го. Это значение используют для определения величины а:

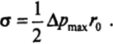
Если диаметр капилляра не очень мал, то для большей точности измерений необходимо вводить поправки на несферичность поверхности пузырька. Как и в ряде других методов, часто прибегают к относительным измерениям, сравнивая результаты с данными для другой жидкости, для которой значение, а известно с высокой точностью.

В методе отрыва кольца (метод Дю-Нуи) измеряется усилие F, необходимое для отрыва от поверхности жидкости тонкого кольца радиуса r_Ki хорошо смачиваемого жидкостью (0 = 0°). В первом приближении можно считать, что связь поверхностного натяжения, а с силой отрыва F определяется выражением, аналогичным тому, которое используется в методе Вильгельми, только вместо ширины пластинки здесь фигурирует длина периметра кольца 2nr_Ki т. е. F= 4яг_ка. Однако на самом деле искривление поверхности жидкости в местах ее соприкосновения с кольцом приводит к тому, что векторы поверхностного натяжения отклоняются от вертикали (рис. 1−34). Кроме того, приходится учитывать роль капиллярного давления, действующего на поверхность кольца и создающего дополнительную.

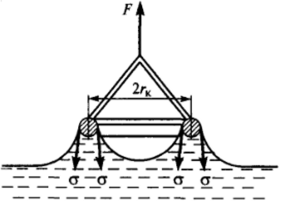
Рис. 1−34. Измерение поверхностного натяжения по методу отрыва кольца.

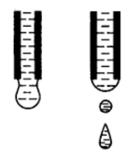
Рис. 1−35. Отрыв капли от торца капилляра.

силу, препятствующую отрыву кольца (подобно капиллярной стягивающей силе менисков). Поэтому для более точных расчетов, а пользуются выражением.

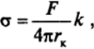
где к — поправочный коэффициент, зависящий от геометрии кольца, может быть найден с помощью специальных таблиц, рассчитанных на основе численного интегрирования уравнения Лапласа.

Метод Дю-Нуи прост в аппаратурном оформлении, достаточно точен и часто используется для определения поверхностного натяжения жидкостей; значительно реже его применяют для определения межфазного натяжения на границе жидкость — жидкость, поскольку в этом случае трудно реализовать условие 0 = 0°.

Широкое применение, особенно для определения межфазного натяжения жидкость — жидкость, получил сталагмометрический метод. Он основан на определении веса капли, отрывающейся под действием силы тяжести от плоской поверхности торцевого среза капилляра (рис. 1−35). Для этого обычно с помощью микрошприца (в более старых конструкциях — под действием собственного веса жидкости) выдавливают определенное число капель исследуемой жидкости и, зная их суммарный вес, вычисляют средний вес одной капли. Теория сталагмометрического метода, связывающая вес отрывающейся капли с поверхностным натяжением, достаточно сложна, но хорошо разработана математически, и данные, необходимые для расчета поверхностного натяжения, табулированы. В самом грубом приближении можно считать, что к моменту отрыва капли ее вес Р уравновешивается силами поверхностного натяжения, равными произведению поверхностного натяжения на длину окружности капилляра: Р= 2ппр. Реальные условия отрыва капли сложнее: перешеек между каплей и частью жидкости, остающейся на конце капилляра, уже диаметра капилляра; кроме того, при отрыве помимо большой капли образуется еще одна или несколько мелких, возникающих при разрыве неустойчивой перемычки между каплей и жидкостью на торце капилляра. Как и в методе отрыва кольца, в уточненное выражение для массы капли вводят поправочный коэффициент к, значения которого рассчитаны и приводятся в таблицах:

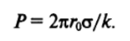
Метод сталагмометрии, особенно с применением электроннооптических устройств для регистрации числа капель, удобен и достаточно точен, что и обусловило его широкое использование в лабораторной практике.

Динамические методы определения поверхностного натяжения имеют более специальное назначение; они применяются в основном для изучения существенно неравновесных состояний поверхностных слоев жидкостей и скорости установления равновесной структуры их поверхности. Это особенно относится к методу колеблющихся струй, позволяющему изучать свойства поверхности жидкости через очень малые промежутки времени после их образования. Суть метода заключается в следующем.

С помощью эллиптического отверстия образуют струю в форме эллиптического цилиндра; под действием сил поверхностного натяжения, стремящихся придать струе форму цилиндра с круговым сечением, и инерционных сил устанавливаются поперечные колебания струи — большая и малая оси эллипса поочередно меняются местами. Теория, развитая Дж. Рэлеем, а затем Н. Бором и Сатерлендом, позволяет связать длину волны на поверхности струи, определяемую экспериментально, с поверхностным натяжением жидкости. Сопоставление полученных таким способом значений поверхностного натяжения с результатами определения их статическим или полустатическим методами позволяет сделать выводы о скорости установления равновесной структуры поверхностных слоев, кинетике адсорбции и т. д. (см. гл. II).

Важную, хотя и трудноразрешимую задачу представляет измерение поверхностной энергии твердых тел. Трудности связаны с тем, что для твердых тел, как правило, не удается реализовать термодинамически обратимое увеличение поверхности раздела фаз, в частности из-за больших необратимых затрат энергии на пластическое деформирование. Тем не менее разработано несколько методов, позволяющих измерять поверхностную энергию твердых тел (или хотя бы оценивать ее).

Для пластичных твердых тел вблизи точки плавления (в основном для металлов) удается реализовать разработанный Тамманом и Удиным метод нулевой ползучести. К тонким полоскам фольги шириной dподвешиваются грузы разного веса (рис. 1−36). Образцы тщательно термостатируются при температуре несколько ниже температуры плавления в течение достаточно длительного времени. Затем измеряется изменение длины образцов А/. В зависимости от веса груза / происходит либо удлинение образцов, либо сокращение их длины под действием силы поверхностного натяжения; обычно наблюдается линейная зависимость удлинения от приложенной силы. Точке пересечения прямой A 1(F) с осью абсцисс («нулевой ползучести») отвечает равенство нагрузки Fсилам поверхностного натяжения по периметру фольги. Точное рассмотрение, учитывающее изменение формы образца при постоянстве его объема, показывает, что в условие равновесия должен быть введен коэффициент /2, так что.

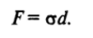
Определенные таким методом значения, а для различных твердых тел приведены в табл. 1.3.

Таблица 1.3. Значения поверхностной энерган а твердых тел, определенные различными методами

‘Условное обозначение методов: н. п.— нулевой полузчести, р. к.— раскалывания кристалла.

В противоположном случае весьма хрупких твердых тел, особенно монокристаллов с хорошо выраженной спайностью, например слюды, удается реализовать предложенный Обреимовым метод расщепления по плоскости спайности. В этом методе обычно изме;

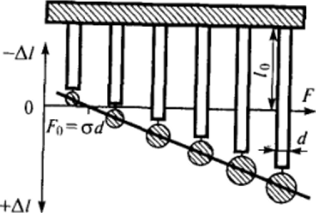
Рис. 1-36. Схема определения поверхностного натяжения методом нулевой ползучести.

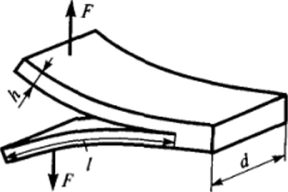
Рис. 1-37. Схема определения поверхностного натяжения методом расщепления монокристалла.

ряется сила Fc, которую необходимо приложить для того, чтобы заранее образованная в твердом теле трещина стала развиваться дальше (рис. 1−37).

Связь силы F_t с поверхностным натяжением а, проявляющимся в данном случае как работа образования новой поверхности, с длиной трещины /, а также толщиной Л, шириной d и модулем Юнга Е отщепляемой пластинки дается уравнением.

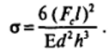
Для определения поверхностной энергии твердых тел используют также зависимость растворимости от размера частиц с привлечением уравнения Томсона (Кельвина). Существенное ограничение на применение этого метода накладывает то обстоятельство, что повышенная растворимость частиц, полученных при механическом измельчении, связана также с появлением в них многочисленных дефектов — упругих и неупругих искажений решетки в результате механического воздействия.

• [1] См. также: Лабораторные работы и задачи по коллоидной химии/Под ред.Ю. Г. Фролова и, А С. Гродского. М., Химия, 1986; Практикум по коллоидной химии/Под ред. И. С. Лаврова. М., Высшая школа, 1983.