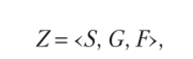Решение задач методом разбиения на подзадачи

Идея метода состоит в следующем. Если путь решения задачи неясен (или неизвестен), то нужно постараться найти какую-то точку опоры, от которой (или до нее) путь известен. Это точка может быть в любом месте — в начале, в середине, в конце, но она должна быть. Этой точке, очевидно, будет соответствовать некоторое состояние на пути от S_n до 5_Ц. Если эта точка 5, — определена, то к ней уже можно применить какое-либо действие и этим изменить состояние предметной области, т. е. приблизиться к возможному решению. Для нового состояния также ищется точка опоры на оставшемся пути, к ней снова применяется какое-то (или то же самое) действие и т. д. — пока не будет решена вся задача.

Чтобы детально описать этот метод, вернемся к определению понятия задачи. Для этой цели воспользуемся понятием пространства состояний. В более общем, чем прежде, виде задачу Z можно представить следующим образом: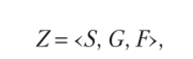

где S — множество начальных состояний; G — множество операторов, переводящих предметную область из одного состояния в другое; F — множество целевых состояний.

При таком обозначении промежуточные состояния 5, — удобнее обозначать через /, поскольку они теперь представляют собой как бы промежуточные цели.

Конечной целью сведения задачи к подзадачам является получение таких элементарных задач, решения которых очевидны. Элементарными считаются задачи, которые могут быть решены за один шаг, т. е. за одно применение какого-либо оператора из множества G.