Граничные условия для векторов В и Н

Рассмотрим магнитное поле вблизи границы раздела двух сред с различной магнитной проницаемостью pi и р₂;

Допустим, что магнитное поле не перпендикулярно границе раздела двух сред.

Разложим векторы В и Н на две компоненты, из которых одна параллельна границе раздела двух сред, а вторая — перпендикулярна. Перпендикулярную компоненту назовём нормальной, а параллельную — тангенциальной.

Начнём с рассмотрения нормальной компоненты вектора магнитной индукции В_п. Воспользуемся для этого теоремой Гаусса для магнитного поля (см. разд. 4.1.10).

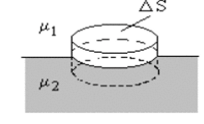
Выделим вблизи границы раздела двух сред цилиндрический объём бесконечно малой высоты с площадью основания AS. Верхнее основание расположено в среде с магнитной проницаемостью р_ь а нижнее — в среде с ц₂ • Согласно теореме Гаусса, магнитный поток через замкнутую поверхность равен нулю.

В данном случае полный магнитный поток через выбранную поверхность равен сумме потоков В_п. через верхнее и нижнее основания и через боковую поверхность цилиндра.

Поскольку высота боковой поверхности бесконечно мала, магнитный поток через неё бесконечно мал. Следовательно, полный магнитный поток равен сумме потоков через верхнее и нижнее основания.

Полный магнитный поток нормальной компоненты вектора магнитной индукции равен нулю, следовательно, потоки через верхнее и нижнее основания равны между собой:

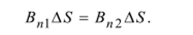
Это означает, что нормальная компонента вектора магнитной индукции на границе раздела двух сред не изменяется:

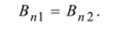
По определению напряжённости В = |д₀ц//, поэтому и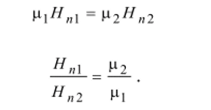

Таким образом, нормальная компонента вектора напряжённости магнитного поля на границе раздела двух сред изменяется. Значение нормальной составляющей напряжённости магнитного поля в средах с разной магнитной проницаемостью различно.

Перейдём к рассмотрению тангенциальной компоненты векторов В и Н. Воспользуемся для этого теоремой о циркуляции вектора напряжённости магнитного поля (см. разд. 4.2.).

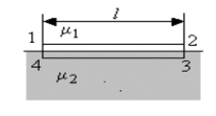
Выделим вблизи границы раздела двух сред замкнутый контур 1−2-3−4 прямоугольной формы (см. рисунок).

Длина горизонтальной стороны прямоугольника равна /, а высота прямоугольника бесконечно мала.

Если на границе раздела двух сред нет тока, то }н^ = 0, т. е. циркуляция вектора напряжённости магнитного поля на границе раздела двух сред равна нулю.

Компоненты циркуляции, но сторонам прямоугольника, перпендикулярным границе разделы, пренебрежимо малы, так как высота прямоугольника бесконечно мала.

Компоненты циркуляции по параллельным сторонам соотвстст;

2 4.

венно равны J Н|<�Л и J Н ₂</1 .

1 3.

Если длина участков 1−2 и 3−4 настолько мала, что напряжённости можно считать постоянными, то н, и Н ₂ можно вынести за знак интеграла. Тогда в результате интегрирования получим векторы 1₁₂ и 1₃₄, направление которых определяется направлением обхода контура.

Таким образом, циркуляция вектора напряжённости на границе раздела двух сред оказывается равной Н, • 1,₂ + Н₂ • 1₃₄ = 0.

Учитывая, что скалярное произведение двух векторов равно произведению их модулей на косинус угла между ними, получаем Я_т1/-//_т2/= 0 (минус обусловлен тем, что векторы 1₁₂ и 1₃₄ противоположны по направлению).

Следовательно, тангенциальная составляющая вектора напряжённости магнитного поля в средах с разной магнитной проницаемостью одинакова: II_т1 = //_т2.

В то же время тангенциальная составляющая вектора магнитной индукции при переходе из одной среды в другую изменяется:

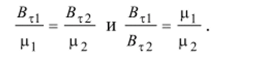
Полученные результаты означают, что силовые линии магнитного поля на границе раздела двух магнетиков преломляются (т. е. изменяют свой наклон):

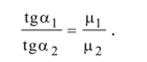aside class="viderzhka__img" itemscope itemtype="http://schema.org/ImageObject">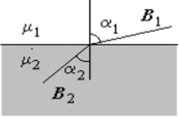

На рисунке показано, что в среде с большей магнитной проницаемостью (|и, > ц₂) силовые линии отклоняются от нормали к границе раздела двух сред (это значит, что их густота увеличивается).

Из полученных результатов также следует, что если в образце магнетика сделать узкую щель, параллельную силовым линиям магнитного поля в веществе, то напряжённость магнитного поля в щели будет равна напряжённости магнитного поля внутри магнетика. Это вытекает из того, что тангенциальная составляющая вектора напряжённости магнитного поля на границе раздела двух сред не изменяется.

Поскольку нормальная составляющая вектора магнитной индукции нс изменяется на границе раздела, значение индукции магнитного поля внутри магнетика и в узкой щели, перпендикулярной направлению магнитного поля, одинакова.

Эти особенности в поведении тангенциальной составляющей напряжённости и нормальной составляющей индукции магнитного поля лежат в основе методов практических измерений напряжённости и индукции магнитного поля внутри магнетиков.