Нормальное распределение. 
Теория вероятностей и математическая статистика

Нормальным законом распределения (законом Гаусса) называют распределение вероятностей непрерывной случайной величины X, если ее плотность вероятности определяется следующей формулой:

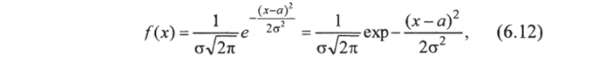
где а и a² = D (X) — параметры распределения, интерпретируемые соответственно как математическое ожидание (среднее значение) и дисперсия случайной величины X.

Соответствующая функция распределения вероятностей случайной величины имеет следующий вид:

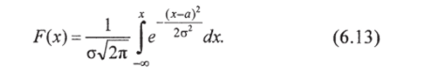
График плотности вероятности /х) и функции распределения F (x) для нормального закона распределения случайной величины X представлены на рисунке.

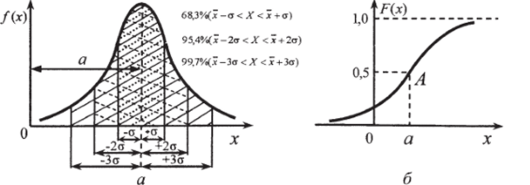
Плотность вероятности/(х) и функция распределения F (x)

Отметим некоторые свойства графика/х).

• 1. График плотности вероятности fix) имеет колоколообразный вид и симметричен относительно прямой х = а.
• 2. В точке х-а функция достигает максимума: f_max = 1/(о/2л).
• 3. Параметр а характеризует форму кривой распределения: чем меньше а, тем «уже» и «выше» график/*).
• 4. На участке от (х-о) до (х+о) размещается 68,3% всех значений*, (х-2о, х+2а) —95,4%, (х-За, х+Зо)—99,7%.

Нормальное распределение с параметрами, а и, а кратко записывается как X~N (a, а). Нормальное распределение X ~ N (a, a)

с параметрами а = 0, а = 1 называется стандартным или нормированным. Обозначение: X~N (0,1).

Функция распределения F (x) случайной величины X~N (a, ст) может быть выражена через функцию Лапласа.

Вероятность того, что случайная величина при нормальном распределении примет значение, принадлежащее интервалу (дц, хт):

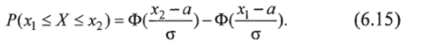
Вероятность того, что абсолютная величина отклонения меньше положительного числа 6 (по абсолютной величине),.

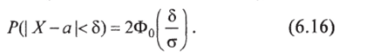
В частности, при а = 0 справедливо равенство.

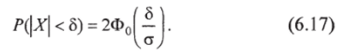
Пример 6.10. Рост взрослых мужчин является случайной величиной, распределенной по нормальному закону. Пусть математическое ожидание равно 170 см, а дисперсия — 36. Найти плотность вероятности этой случайной величины. Вычислить вероятность того, что хотя бы один из наудачу выбранных четырех мужчин будет иметь рост от 168 до 172 см.

Решение. Пусть случайная величина X выражает рост взрослых мужчин, Х -из наудачу выбранных четырех мужчин имеет рост от 168 до 172 см.

По условию математическое ожидание а=170, а дисперсия ?> = 36. Отсюда среднее квадратичное отклонение.

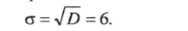
Следовательно, искомая плотность вероятности.

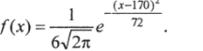
Воспользуемся формулой.

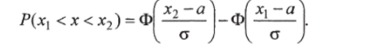
Подставив Х = 168, *2 = 172, а- 170, о = 6, и учитывая свойство функции Лапласа Ф (-х) = - Ф (х), получим.

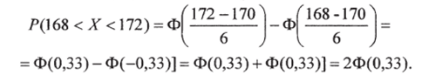
По таблице прил. 2 находим 2Ф (0,33) = 2 • 0,1293 = 0,2586.

Таким образом, вероятность того, что случайно выбранный мужчина имеет рост от 168 до 172 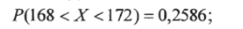см Обозначим A_hA₂, A₃ и Л₄ — события, состоящие в появлении мужчин с ростом от 168 до 172 см соответственно в первом, втором, третьем и четвертом испытаниях. Эти события независимы в совокупности и имеют одинаковую вероятность:

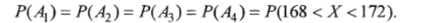
По формуле (3.8) искомая вероятность того, что хотя бы один из наудачу взятых четырех мужчин имеет рост от 168 до 172 см равна.

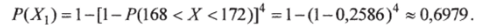
Пример 6.11. Исследования показали, что здоровые люди в значительной мере отличаются по содержанию в крови фермента каталазы. В табл. 6.6 приведены данные обследования 1000 людей. Определите математическое ожидание и среднее квадратичное отклонение фермента каталазы. Сравните данные распределения с нормальным законом, имеющим те же параметры (М и о).

Таблица 6.6. Содержание в крови фермента каталазы.

Решение. Составим расчетную таблицу 6.7, для этого:

• 1) запишем числовые значения случайной величины X (содержание фермента каталазы в крови) во вторую строку;
• 2) запишем вероятности в третью строку; в последнем столбце помещаем накопленную вероятность событий (контроль: 0,04 + 0,1 + 0,2 + 0,3 + 0,2 + 0,12 + 0,04 = I);
• 3) произведения вероятности р, на значения х, запишем в четвертую строку; сумму чисел строки (т.е. математическое ожида-

П ние М (Х) = ^?^р₁х,)) помещаем в последнем столбце;

>>1.

4) произведение вероятности р, на квадрат отклонения случайной величины х, от ее математического ожидания М (Х) запишем в пятую строку; сумму чисел строки (т.е. дисперсию) помещаем в последнем столбце.

В итоге получаем следующую расчетную табл.6.7:

Таблица 6.7. Результаты расчета параметров распределения.

По данным таблицы находим параметры распределения:

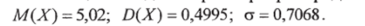
Далее составим статистическое распределение фермента каталазы в крови (табл. 6.8). Для этого:

• 1) минимальные значения границы х* каждого из равноотстоящих интервалов (ширина шага Лх = 0,5) запишем во вторую строку: здесь следует считать каждое значение х‘ граничным для соответствующего интервала (например, среднюю х, =3,5 относить к интервалу 3,25 < х, < 3,75 и х* = 3,25);
• 2) используя параметры распределения (М, D и а), вычислим значения z, соответствующие границам интервалов z, =(х,-М)1а, которые поместим в третью строку; найденные по таблице прил. 2 значения Ф (г,) запишем в четвертую строку.

В итоге получим сводную табл. 6.8.

Таблица 6.8. Значения границы равноотстоящих интервалов и Ф (г/).

Используя данные таблицы, найдем вероятность попадания случайной величины X в первый интервал (со средним — 3,5):

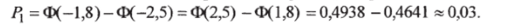
Аналогично вычислим вероятности попадания X в остальные интервалы:

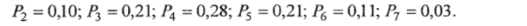
Сравнив наблюдаемые значения Р, с вероятностями р, соответствующих интервалов, делаем вывод о почти точном совпадении теоретического (нормального) и полученного на опыте эмпирического распределения. Следовательно, содержание в крови фермента каталазы является случайной величиной X, распределенной по нормальному закону.

Пример 6.12. Производится взвешивание лекарственного препарата без учета систематических погрешностей измерений. Случайные погрешности взвешивания подчинены нормальному закону со средним квадратичным отклонением ст = 20 г. Найти вероятность того, что взвешивание будет произведено с абсолютной погрешностью, не превосходящей по абсолютной величине i0 г.

Решение. Если в формулу (6.16) подставить значения о = 20 и 5 = 10, то получим вероятность того, что взвешивание будет произведено с абсолютной погрешностью 5 измерения, не превосходящей заранее заданного значения:

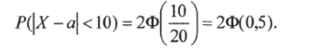
По таблице прил. 2 находим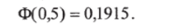

Таким образом, искомая вероятность.

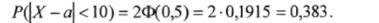
Пример 6.13. Длина скальпеля X представляет собой случайную величину, распределенную по нормальному закону распределения и имеет среднее значение 150 мм, а среднее квадратичное отклонение — 0,2 мм. Необходимо: а) записать выражение плотности распределения; б) найти вероятность того, что длина скальпеля будет заключена в интервале от 149,7 до 150,3 мм; в) найти вероятность того, что величина отклонения (абсолютная погрешность) не превышает 0,1 мм; г) найти, каким должно быть задано отклонение, чтобы процент скальпелей, отклонение которых от среднего не превышает заданного, повысился до 54%.

Решение. а) Подставляя исходные данные в формулу (6.12), полагая при этом гаг = 150, а = 0,2, получим выражение для плотности вероятности случайной величины X

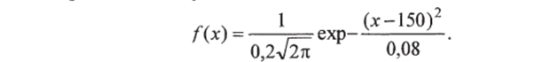
б) Вероятность того, что длина скальпеля окажется в пределах от 149,7 до 150,3 мм, по формуле (6.15) равна.

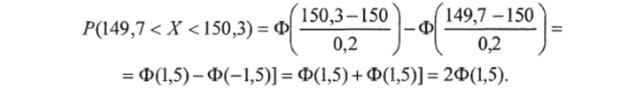
По таблице прил. 2 находим Ф (1,5) = 0,4332, отсюда искомая вероятность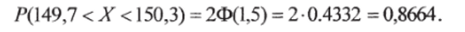

в) По формуле (6.16) найдем вероятность того, что величина отклонения не превышает заданного значения.

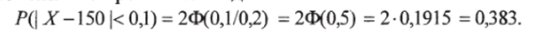
г) По условию процент скальпелей, отклонение которых от среднего не превышает заданного, повысился до 54%.

Поэтому можно записать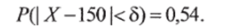

g.

С другой стороны, Р (X -1501< 5) = 2Ф (—), следовательно, а.

• 6 5
• 2Ф (—) = 0,54, а значит Ф (—) = 0,27. В таблице прил. 2 находим, а а

Ъ 6.

значение аргумента функции Ф (—), которое равно — = 0,74. От;

а, а сюда искомое отклонение Ъ = 0,74ст = 0,74 • 0,2 = 0,15 мм.