Задание.
Моделирование электромеханических систем

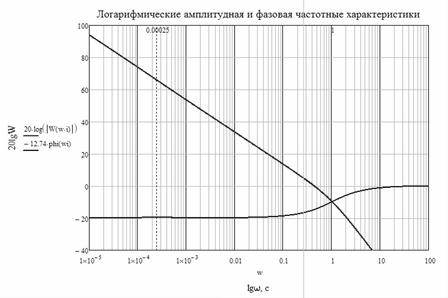
Анализируя влияние квантования сигнала по времени и сравнивая период дискретизации сигнала и величину постоянных времени объекта управления, можно определенно сказать, что исследуемую систему следует рассматривать как непрерывную, так как > Так как модуль передаточной функции звена запаздывания всегда равен единице, то исходная ЛАЧХ не изменится, запаздывание изменит лишь ЛФЧХ (рис. 10). Фазовая… Читать ещё >
Задание. Моделирование электромеханических систем (реферат, курсовая, диплом, контрольная)
Выполнить сравнительный анализ динамических возможностей систем регулирования.
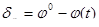
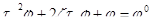
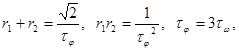
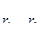
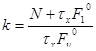
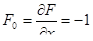
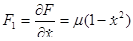
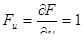
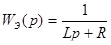
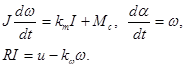
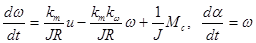
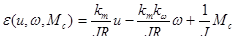
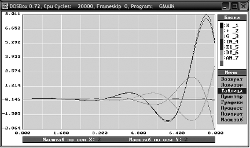
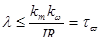
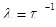
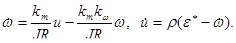
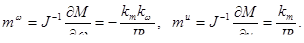
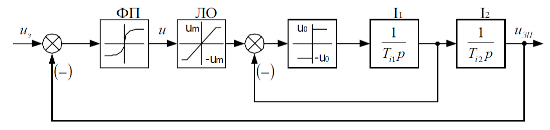
Рисунок 10.1 — Структурная схема.
Звено чистого запаздывания. Это звено без искажения воспроизводит на выходе входную величину, как идеальное пропорциональное звено, но с той разницей, что выходная величина запаздывает относительно входной на постоянное время. Уравнение такого звена имеет вид:
где — время запаздывания.
Очевидно, характеристики этого звена будут:
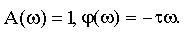
Отсюда АФЧХ:
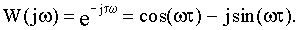
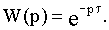
В качестве примера звена можно назвать длинную электрическую линию без потерь, механический транспортер и т. д.
По существу, это звено относится к нелинейным. Однако при расчетах САУ с такими звеньями можно применять методы теории линейных систем. Поэтому часто элементы, закон движения которых мало изучен или трудно представим в аналитической форме, после некоторой идеализации представляются в виде звеньев запаздывания.
Оценка влияния запаздывания ОИ на величину критического коэффициента Нам известна величина времени запаздывания объекта исследования:.
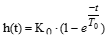
С его учетом изменим передаточную функцию разомкнутой системы.
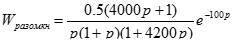
.
Так как модуль передаточной функции звена запаздывания всегда равен единице, то исходная ЛАЧХ не изменится, запаздывание изменит лишь ЛФЧХ (рис. 10). Фазовая характеристика пересекает ось на частоте, меньшей частоты среза. Система неустойчива.
Рассчитаем переходную характеристику замкнутой САУ с учетом запаздывания. Для этого построим в программе модель системы, состоящую из усилителя с коэффициентом Р1 =0,05, интегратора, упругого звена (Р1=4000, Р2=4200), звена запаздывания (Р1=0, Р2=100) и линейного звена (Р1=1, Р2=1). Подаем на вход сигнал в виде единичной ступенчатой функции —. В весовом сумматоре, которым пользуемся для создания ООС, задаем следующие коэффициенты —, , (т.е. на 3-ий вход сумматора подаем инвертируемый сигнал с выхода системы).
Обозначаем выходы системы.
Переходим к расчету переходной характеристики.
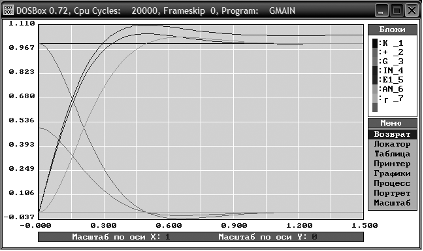
Полученная переходная характеристика показана на рис. 12. Как и предполагалось, система потеряла устойчивость.
Понизим коэффициент для более подробной оценки влияния запаздывания.
Примем .
Переходная характеристика показана на рис. 13. Она имеет колебательный характер. Перерегулирование составляет 45%, время регулирования 863 секунды.
Примем .
Переходная характеристика показана на рис. 14. Она имеет колебательный характер, запаздывает на 100 секунд. Перерегулирование 3,3%, время регулирования 360 секунд.
Для определения напряжения на зажимах двигателя в любом режиме его работы необходимо рассчитать полное сопротивление двигателя Zдв, полное сопротивление линии Zл и эквивалентное сопротивление.
Zэ = Zл + Zдв.
по схеме замещения на рис. 1.
Сопротивление двигателя в комплексной форме:
Zдв = (R0+jХ0)(R11+jХk)/(R0+R11) j (Х0 + Хk)= Rдв +jXдв=1,302+j0,719 ,.
где:
Rдв = (R20 R11 +R0 R211 +Х20R11 + Х2k R0) /(R0 +R11) 2+ (Х0 + Хk) 2=1,302, Ом;
Xдв = (X20Xk+ X2k X0 + R20Xk +R211Х0) /(R0 + R11)2+ (Х0 + Хk) 2=0,719;
R11 = R1+ R2/s=0,134+0,018/0,017=1,704.
Z11 ==1,725 Ом.
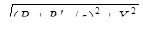
Тогда.
Z’дв =Zдв е j дв=1,487Ґе j0,505.
где:
Zдв ==1,487 Ом;
дв = arctg (Хдв/Rдв)=0,505.
Эквивалентное сопротивление:
Zэ = Zл + Zдв =Z'э е jэ=1,49Ґе j0,505=2,47,.
где:
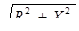
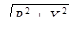
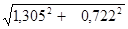
Z’э ===1,49.
Rэ =Rл + Rдв=1,305.
Хэ = Xл + Xдв=0,722.
э = arctg (Хэ/Rэ)=0,505.
Ток, потребляемый двигателем из сети:
I1ф = Uсфн/ Z11 = 147, А, где:
Uсфн = U1фн /()1-В.
— номинальное фазное напряжение в питающей сети.
Напряжение на зажимах двигателя:
U1ф = I1ф Zдв = 147Ґ1,487=218,8, В.
Потери напряжения в линии:
U1 = Uсфн, — U1ф = 219,39 -2 18,8=0,591 В.
Ток рабочей ветви:
I2ф= U1ф/ Z11 = 218,8/1,725=127, A,.
Электромагнитная мощность:
Рэ = 3· I22ф (R2/ s) =3Ґ1272 Ґ(0,026/0,017) = 75 820, Вт.
Активная мощность на валу двигателя:
Р2 = Рэ (1- s)=75 820Ґ(1−0,017)=74 556, Вт.
Активная мощность, потребляемая двигателем из сети:
Р1= 3· U1ф I1ф cosдв =84 726 Вт.
Потеря активной мощности определяется:
Р = Р1 — Р2 = 84 726 — 75 556 = 9 170 Вт.
Реактивная мощность, потребляемая двигателем из сети:
Q1= 3· U1ф I1ф sinдв = 46 816 вар.
Полная мощность, потребляемая двигателем из сети:
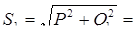
96 831, кВА.
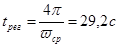
В контуре управления анализируемые системы содержат микропроцессорные устройства, работающие с дискретными сигналами, т. е. такие системы являются не непрерывными, а дискретно — непрерывными. Микропроцессорные устройства квантуют непрерывный сигнал и по уровню и по времени. Квантование по уровню происходит потому, что амплитуда дискретного сигнала ограничена некоторой совокупностью значений, определяемой разрядностью микропроцессора. Но квантование по уровню по сравнению с квантованием по времени создает на выходе эффект второго порядка малости, поэтому обычно при рассмотрении динамики системы в первом приближении квантованием по уровню пренебрегают.
Анализируя влияние квантования сигнала по времени и сравнивая период дискретизации сигнала и величину постоянных времени объекта управления, можно определенно сказать, что исследуемую систему следует рассматривать как непрерывную, так как >.
Структурная математическая модель непрерывной системы управления термическим оборудованием с пропорциональным законом регулирования показана на рисунке ниже.
Математическое моделирование показателей рабочих и энергетических характеристик АД производится по известной математической модели и методике 1.
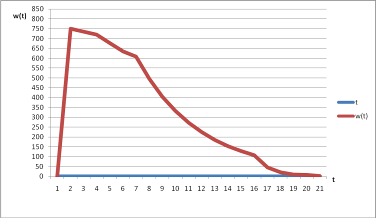
Рисунок 10.2. Весовая характеристика апериодического звена второго порядка.
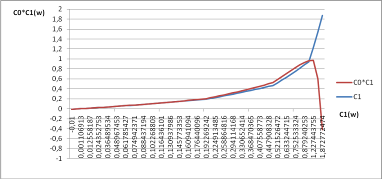
График зависимости С1С0 = f (C1) для ПИ — регулятора.
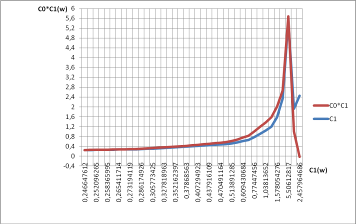
График зависимости С1С0 = f (C1) для ПИД — регулятора При математическом моделировании показателей рабочих и энергетических характеристик АД задаются скольжением s=(0,25; 0,5; 0,75; 1,0; 1,25)*sн и напряжением.
U1=(0.8; 0.85; 0.9; 1.0; 1.05; 1.1)*U1.
и определяют cos;; n2; M; I1ф; U1; Р1; Р2; Q1; S1; Q1c; S1c; Р; U (табл.2 и 3) Величина потери напряжения U не должна превышать (-0,05…+0,1)Uн [2].
По данным вычислений (таблица 5) строят: рабочие характеристики двигателя Р1; cos;; M; I; n2; s =f (P2) и оценивают потерю напряжения в питающей линии.
Энергетические характеристики асинхронного электродвигателя и ЛЭП строятся по значениям, которые приведены в таблице 5: U1; Р1; Р2; Q1; S1; Q1c; S1c; Р; U; cos; = f (U1).