Метод скользящей средней

Основан на вычислении средних величин за укрупненные периоды времени. Цель — абстрагироваться от влияния случайных факторов, взаимопогасить их влияние в отдельные годы.

Для расчета используют следующий алгоритм.

• 1. Определяют длину интервала сглаживания /, включающего в себя / последовательных уровней ряда (/ < п). При этом надо иметь в виду, что чем шире интервал сглаживания, тем в большей степени взаимопогашаются колебания и тенденция развития носит более плавный, сглаженный характер. Чем сильнее колебания, тем шире должен быть интервал сглаживания.
• 2. Разбивают весь период наблюдения на участки, при этом интервал сглаживания как бы скользит по ряду с шагом, равным /.
• 3. Рассчитывают средние арифметические из уровней ряда, образующих каждый участок.
• 4. Заменяют фактические значения ряда, стоящие в центре каждого участка, на соответствующие средние значения.

При этом удобно брать длину интервала сглаживания / в виде нечетного числа: 1= 2р + 1, так как в этом случае полученные значения скользящей средней приходятся на средний член интервала. Наблюдения, которые берутся для расчета среднего значения, называются активным участком сглаживания.

При нечетном значении / все уровни активного участка могут быть представлены в виде.

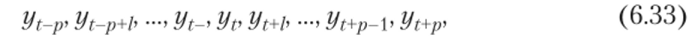
где y_t — центральный уровень активного участка; y_t__p, y_t__p+i — последовательность из р уровней активного участка, предшествующих центральному; у_1Ур-1, y_t+p — последовательность из р уровней активного участка, следующих за центральным.

Тогда скользящая средняя рассчитывается по формуле.

где у_{ — фактическое значение /-го уровня; y_t — значение скользящей средней в момент t 2р + 1 — длина интервала сглаживания.

Процедура сглаживания приводит к устранению периодических колебаний во временном ряду, если длина интервала сглаживания берется равной или кратной периоду колебаний. Для устранения сезонных колебаний часто требуется использовать четырехи двенадцатичленные скользящие средние, но при этом не будет выполняться условие нечетности длины интервала сглаживания. Поэтому при четном числе уровней принято первое и последнее наблюдение на активном участке брать с половинными весами:

Тогда для сглаживания сезонных колебаний при работе с временными рядами квартальной или месячной динамики можно использовать 4- и 12-членные скользящие средние:

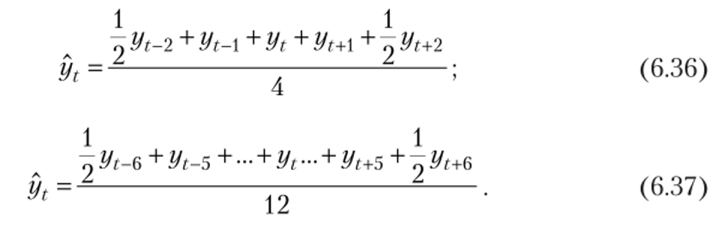
В формуле с четырехчленным скользящим средним каждый активный участок содержит пять уровней, в формуле с 12-членным — 13 уровней, при этом крайние уровни имеют половинные весовые коэффициенты.

При использовании скользящей средней с длиной активного участка / = 2р + 1 первые и последние р уровней ряда сгладить нельзя, их значения теряются. Очевидно, что потеря значений последних точек является существенным недостатком, так как для исследователя последние «свежие» данные обладают наибольшей информационной ценностью.

Рассмотрим один из приемов, позволяющих восстановить потерянные значения временного ряда при использовании простой скользящей средней. Для этого необходимо следующее.

• 1. Вычислить средний абсолютный прирост на последнем активном участке.
• 2. Получить р сглаженных значений в конце временного ряда путем последовательного прибавления среднего абсолютного прироста к последнему сглаженному значению.

Аналогичную процедуру можно реализовать для оценивания первых уровней временного ряда.

Метод простой скользящей средней применим, если графическое изображение динамического ряда напоминает прямую. Когда тренд выравниваемого ряда имеет изгибы и для исследователя желательно сохранить мелкие волны, то применение простой скользящей средней нецелесообразно.

Если для процесса характерно нелинейное развитие, то простая скользящая средняя может привести к существенным искажениям. В этих случаях следует использовать взвешенную скользящую среднюю.

При построении взвешенной скользящей средней на каждом активном участке значение центрального уровня заменяется на расчетное, определяемое по формуле средней арифметической взвешенной.

где — весовые коэффициенты.

Простая скользящая средняя учитывает все уровни ряда, входящие в активный участок сглаживания, с равными весами (w), а взвешенная средняя приписывает каждому уровню вес, зависящий от удаления данного уровня до уровня, стоящего в середине активного участка. Это вызвано тем, что при простой скользящей средней выравнивание на каждом активном участке производится по прямой (полиному первого порядка), а при сглаживании по взвешенной скользящей средней используются полиномы более высоких порядков, чаще всего 2-го или 3-го порядка. Поэтому метод простой скользящей средней может рассматриваться как частный случай метода взвешенной скользящей средней.

Отметим важные свойства весовых коэффициентов:

• — они симметричны относительно центрального уровня;
• — сумма весов с учетом общего множителя, вынесенного за скобки, равна единице;
• — наличие как положительных, так и отрицательных весов позволяет сглаженной кривой сохранять различные изгибы кривой тренда.

В табл. 6.10 приведены фактические данные о динамике ВВП в России за 1995—2013 гг. и расчеты по выравниванию этого ряда тремя методами.

Таблица 6.10

Выравнивание данных о динамике ВВП России за период 1995— 2013 гг. методами укрупнения интервалов, скользящей средней и аналитического выравнивания