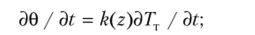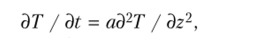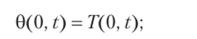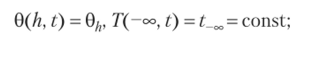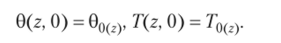Физико-математическая постановка задачи прогноза температуры в термодинамической системе «приземной слой воздуха — подстилающая поверхность»

Если рассматривать подстилающую поверхность как однородное бесконечное полупространство, в котором имеет место однородный поток тепла, то процесс теплообмена подстилающей поверхности с приземным слоем воздуха описывается системой из двух уравнений:

— турбулентной теплопроводности для воздуха.

— кондуктивной теплопроводности для подстилающей поверхности.

где k (z) — коэффициент турбулентности воздуха, зависящий от координаты z — расстояния от земной поверхности, м²/ч; а = Л,/су — коэффициент температуропроводности, м²/ч.

Совместные решения этих уравнений находятся при следующих краевых условиях:

— на границе обеих сред при z = 0 должно удовлетворяться уравнение теплового баланса.

— условие непрерывности температуры при переходе через поверхность имеет вид.

— на высоте z = h и z = температуры равны своим средним значениям:

В приведенных формулах приняты следующие обозначения: X, су — коэффициент теплопроводности и объемная теплопроводность подстилающего грунта; у_вс_в — объемная теплопроводность приземного слоя воздуха.

Решение данной системы дифференциальных уравнений при рассмотренных краевых условиях, достаточно полно отражающих физические процессы, происходящие в системе «приземной слой воздуха — подстилающий грунт», получено методом последовательных приближений для T (z, t) и 0(2, t).

В связи со значительными трудностями практической реализации данной задачи в рассмотренной постановке, прежде всего из-за того, что теплофизические характеристики воздуха и слоистой конструкции являются функциями координат ги?, часто ограничиваются решением только одного уравнения для подстилающего грунта, задаваясь граничным условием на поверхности 'ДО, t.) = f (t) — в виде функции, являющейся результирующей теплообмена на границе «грунт — воздух».

При краткосрочных прогнозах функция f (t) задается в виде гармонических колебаний с циклом t = 24 ч вида.

где со = 2л/24 — круговая частота.

Если необходимо прогнозировать температурный режим в дорожной конструкции на срок более одних суток, то граничное условие на поверхности задается в виде сложной гармонической функции.