Выталкивающая сила. 
Закон Архимеда

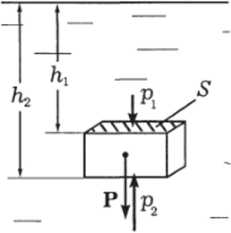
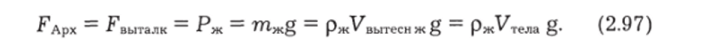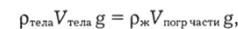На погруженное в жидкость тело действует выталкивающая сила, обусловленная тем, что нижняя поверхность тела (рис. 2.57) находится на большей глубине Ьг, чем верхняя h. В результате разности этих давлений выталкивающая сала равна весу жидкости, вытесненной телом (закон Архимеда):

Если вес тела Р > F_Apx, то оно тонет, если Р < Fa_Px, — всплывает, а при Р = Р_Арх находится в состоянии безразличного равновесия в любой точке жидкости.

Это относится и к воздушным шарам в атмосфере, но с двумя поправками. Во-первых, давление в атмосфере меняется с высотой по.

другому закону (см. раздел 1 главы 3), вовторых, газ в шаре легко сжимается и расширяется, так что давление внутри него всегда почти равно давлению снаружи. В результате шар при подъеме либо раздувается, увеличивая свой объем, либо при твердой оболочке выпускает часть газа. Попробуйте составить программу для компьютера для расчета подъема шара.

Если тело плавает и над поверхностью жидкости находится некоторая его часть, а под ней остается объем погруженной части V_n0r_P (рис. 2.58), то условием равновесия будет равенство силы притяжения к Земле и выталкивающей силы Архимеда:

так что = р"."/р_ж. Например, плотность льда составляет 0,9 от плотности воды и под уровнем воды будет 0,9 от всего объема льдины, а сверху — только одна десятая часть.

Пример. Рассмотрите приведенную в пакете ПАКПРО программу Arh.imed.pas в каталоге MechMech_spl_sr. Запустите ее в работу, разберитесь, как программа отвечает на ваши вопросы.