Вероятностно-экономическая модель. 
Управление запасами в цепях поставок

В основу данной модели оптимизации размера страхового запаса положена зависимость для общих затрат, в которой рассматриваются только два слагаемых: затраты на хранение CX (Q) и издержки дефицита Сд (.

Входящие в формулу (6.18) затраты на хранение C_X(Q) могут быть представлены в виде.

где с_х — затраты на хранение единицы продукции в единицу времени.

Для расчета издержек, связанных с дефицитом, в общем случае используется зависимость где с_д — издержки из-за дефицита, руб/ед. • год; 1(х_р) — функция или интеграл потерь.

Для нормального закона распределения значения 1(х_р) — табулированы (прил. 1).

При подстановке (6.19), (6.20) в формулу (6.18) получим.

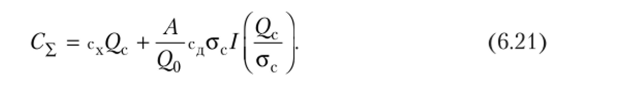
Очевидно, что искомая величина страхового запаса Q. входит неявно в функцию потерь. Поэтому для расчета Q следует воспользоваться численным методом. Покажем это на примере.

? Разбор ситуации Предположим, что специалист по управлению запасами имеет следующие данные: потребность в продукте А = 1200 ед., оптимальная партия поставки (2о = ЮО ед.; затраты на хранение единицы продукта с_х= 50 руб/ед. • год; потери из-за дефицита оцениваются в размере с_д = 100 руб/год; ст_с = 20 ед. Специалист рассчитал, что страховой запас должен быть Q. - 21 ед. Каковы будут затраты, связанные со страховым запасом? Правильно ли с точки зрения минимума затрат специалист определил размер страхового запаса?

Для страхового запаса в 21 ед. х_р = — = 1,037, а интеграл потерь /(1,037) =.

= 0,0776. Подставим имеющиеся данные в (6.21) и найдем суммарные затраты, связанные со страховым запасом:

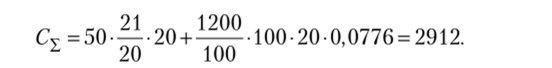
В табл. 6.2 приведены результаты расчетов для других значений страхового запаса. Она показывает, что минимальные суммарные издержки С_г = = 2139 руб. соответствуют страховому запасу Q.= 35 ед.

Таблица 6.2

Расчет оптимальной величины страхового запаса.

* Оптимальная величина страхового запаса.

Воспользовавшись прил. 1, определим вероятность отсутствия дефицита при Qc = 35 ед.:

Рассчитаем также «коэффициент удовлетворения спроса»¹, или «уровень доступности запасов»^[1][2]:

Таким образом, при условии минимума издержек страховой запас составит Q. = 35 ед., вероятность отсутствия дефицита Р ( 1,75) = 0,98, а коэффициент удовлетворения спроса FR = 0,9958. Это означает, что из 1000 ед., запрошенных потребителем, 997 будут готовы к продаже.

Как видно из расчетов, специалист по управлению запасами определил неоптимальное значение страхового запаса с точки зрения минимума общих затрат, связанных со страховым запасом. Его решение вызовет снижение коэффициента удовлетворения спроса.

? Научная дискуссия Для оценки величины страхового запаса в условиях неопределенности Д. Дж. Бауэрсоксом и Д. Дж. Клоссом^[3] рекомендована формула.

где k — коэффициент, определяемый с помощью табулированной функции потерь I (k); а₍. — среднее квадратичное отклонение, формула (6.5).

Для расчета входящей в формулу функция I (k) предлагается воспользоваться зависимостью.

При подстановке /(1,75) получим.

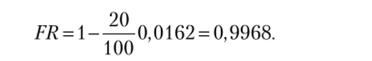
где S_L — величина дефицита; Q — размер заказа.

Пример. Рассчитаем страховой запас поданным, приведенным в работе Д. Дж. Бауэрсокса и Д. Дж. Клосса: Q = 300 ед.; S_L = 0,99; 7 = 10 дн.; о_т = = 2 дн.; D = 5 ед.; ст₀ = 2,54 ед. По формуле (6.5) находим.

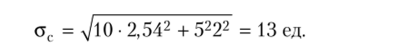
Затем по формуле (6.24).

и, наконец, по формуле (6.21) при k = 0,4 (см. табл. 6.3).

Таким образом, страховой запас в 5 ед. «обеспечивает насыщение спроса клиентов на 99% при размере заказа 300 ед.».

В табл. 6.3 приведены результаты расчетов также при других размерах заказа: 200 и 100 ед. Из нее следует парадоксальный вывод: чем меньше размер заказа Q, гем больше страховой запас Остр;

Поскольку в комментариях к формулам ничего не говорится об ограничениях, то был проведен расчет при Q = D = 5 ед., т. е. при Т = 1 день. Величина запаса составила Q<- = 29,6 ед., следовательно, превзошла среднюю ежедневную поставку в 6 раз!

Таблица 63

Зависимость страхового запаса от размера заказа

Примечание. При Q= 100, 200 и 300 результаты взяты из работы Д. Дж. Бауэрсокса и Д. Дж. Клосса, остальные расчеты выполнены авторами.

Полученные результаты настораживают не только с точки зрения страхового запаса, но и возможной вариации «величины дефицита» S_L. Так, при Q = 300 ед., а_с = 13 ед. варьирование значений функции /(к) от 0,3989 до 0,0003 в (6.24) привело к изменению S_L всего на 0,017, т. е. от S_f = 0,983 до S_L = 1,00. Но не поддается объяснению область значений, когда «величина дефицита» S_r становится меньше нуля, что противоречит физической сущности данной вероятностной характеристики. Например, в анализируемом примере при /(к) = 0,4 и Q = 5 ед. находим.

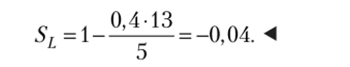
Попытаемся объяснить возникновение данного «парадокса» с помощью рис. 6.4.

В работе американских специалистов расчет страхового запаса произведен при Q = 50 ед., Т = 10 дн. В этом случае при заданной вероятности Р разбросу случайных величин времени цикла Т соответствует линия А, которая может быть названа базовым уровнем (см. рис. 6.4).

Перенесем нулевой уровень вверх по вертикальной оси (0'), тем самым уменьшая Т. Учитывая, что для реализации ежедневного расхода наблюдается сильное перемешивание, и данные реализации расходятся в виде «пучка», ограниченного линиями QqF, разбросу случайных величин Тбудет соответствовать линия С. Если перенести нулевой уровень в точку 0″, то продолжительность цикла возрастает, и разбросу случайных величин Т будет соответствовать линия D.

Таким образом, некорректность расчета по (6.5) состоит в том, что для разных Q и, соответственно, Т подставляется одно и то же значение а_г, поэтому разброс случайных величии Т ограничен параллельными линиями В.

Важно запомнить

Формула (6.5) будет верна в случае, если вместо Т и а_ш, соответствующих базовому уровню, будут подставлены среднее и среднее квадратическое отклонение новой продолжительности цикла заказа (L, g_l).

Если для новых условий нет данных для определения статистических параметров продолжительности функционального цикла, то для учета изменившихся условий следует ввести в расчет параметр, позволяющий учесть подобие (подобие треугольников на рис. 6.4). В качестве такого параметра может использоваться коэффициент вариации.

Допустим, что статистические_параметры, характеризующие ежедневный расход (или объем продаж), D и a_D — постоянны и не зависят от продолжительности цикла Г; закон распределения ежедневных продаж — нормальный. Для продолжительности цикла, подчиняющегося нормальному закону, среднее значение равно Г, а среднее квадратическое отклонение.

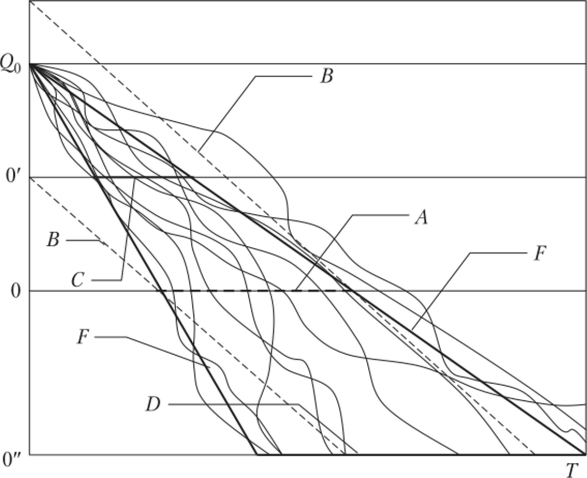
Рис. 6.4. Графическая интерпретация корректировки формулы (6.5)^1.

где u_r — коэффициент вариации, определенный на основе статистической обработки для базовой выборки.^[4]

Например, если статическая информация собрана для базового уровня цикла заказа с параметрами Т = 10 дн., а_т = 2 дн. и х>_т= 0,2, то для цикла с L — 20 дн., соответственно, a_{L = 2}о ⁼ 0"2 • 20 = 4 дн.

Таким образом, формула (6.5) может быть записана в виде.

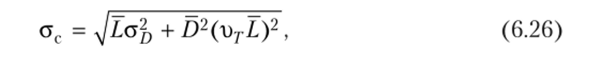
где L — среднее значение продолжительности цикла заказа, отличное от базового уровня.

Справедливость (6.26) была_доказана с помощью имитационного моделирования при различных Q, L, v_r, результаты которых оказались близкими к полученным по (6.26).

• [1] Сток Дж. Р., Ламберт Д. М. Стратегическое управление логистикой.
• [2] Бауэрсокс Д. Дж., Клосс Д. Дж. Логистика. Интегрированная цепь поставок. 2-е изд.М.: Олимп-Бизнес, 2005.
• [3] Бауэрсокс Д. Дж., Клосс Д. Дж. Логистика. Интегрированная цепь поставок.
• [4] Модели и методы теории логистики / под ред. В. С. Лукинского. 2-е изд. С. 293.