Закон толерантности. 
Математические методы в биологии и экологии. 
Биофизическая динамика продукционных процессов. 
Часть 1

Наряду с законом лимитирования в моделировании экологических систем часто применяется принцип совокупного действия факторов. Согласно этому принципу, для существования любой системы необходима совокупность факторов, каждый из которых имеет некоторые пределы, в которых живая система может существовать. Таким образом, существует многомерная область параметров — величин этих факторов, допустимых дтя жизни живой системы (организма, вида, биогеоценоза). Это и есть область тех значений факторов, к которым живая система толерантна.

Для исследования зависимости реакции экологической системы от тех или иных факторов в современной науке используют метод функций отклика. Этот метод широко применяется в инженерных науках, например, теории автоматического регулирования или теории планирования эксперимента. Его суть заключается в использовании информации об отклике системы на известные воздействия для получения оператора перехода по схеме: воздействие — реакция. В терминах теории сложных систем динамика сложной открытой системы, каковой является экосистема, характеризуется описанием связи между входными и выходными сигналами.

Идея функций отклика восходит к работам немецкого агрохимика Митчерниха и была им сформулировала в начале века как «закон физиологических взаимосвязей» (Mitchernich et al., 1921). Митчерних утверждал, что величина урожая зависит от уровней всех факторов роста, и тем самым противопоставлял свой закон принципу минимума Либиха.

Американский ученый В. Шелфорд в 1913 г. сформулировал «закон толерантности», утверждающий, что как недостаток, так и избыток любого внешнего фактора (для растения — азота, фосфора, света, углекислого газа и пр.) может быть вредным для биологического объекта (организма, популяции) (Shelford, 1929). Доказательством этого служит факт, что функции отклика — зависимости количественных оценок тех или иных характеристик популяций от важнейших факторов внешней среды (содержания питательных веществ, температуры) — имеют колоколообразную форму. Пределы, в которых может существовать живой организм, называют диапазоном толерантности. Тогда под лимитирующим фактором понимается тот, который приближается или выходит за пределы толерантности.

В экологической литературе (Одум, 1975; Федоров, Гельманов, 1980; Левич и др., 1997) закон толерантности рассматривается как продолжение и расширение принципа Либиха. Лимитирующим при этом называют фактор, по которому для достижения заданного относительного изменения функции отклика необходимо минимальное относительное изменение значения фактора. Такое определение требует подробного изучения зависимости функций отклика от всей совокупности экологических факторов в каждом конкретном случае, что связано с использованием приемов многофакторного эксперимента и аппарата многомерной математической статистики. Практическое использование такого подхода к исследованию большинства природных экосистем затруднено из-за недостатка экспериментальных данных и отсутствия систематических наблюдений.

Применение метода функций отклика для описания сложных экологических систем подразумевает решение задачи идентификации параметров нелинейных систем достаточно большой размерности. Это стало возможным лишь в последние десятилетия XX в. в связи с появлением принципиально иовьгх возможностей обработки временных рядов, новых пакетов решения систем дифференциальных уравнений, новых оптимизационных пакетов для проведения процедуры идентификации параметров, новых информационных технологий. Важным вопросом моделирования систем на основе метода функций отклика является анализ и обработка экспериментальных данных и использование робастных процедур, приводящих к тому, что результаты обработки мало зависят от наличия данных с большими ошибками.

Сложность экологических систем приводит к тому, что функциональную связь между компонентами системы трудно описать традиционными методами, которые используются, например, в классических задачах динамики популяций или работах по описанию распространения загрязнений с помощью уравнений гидрои аэродинамики. Если не удается описать функциональную связь в «простых» и известных науке терминах, исследователи прибегают к аппроксимации этой функциональной связи на основе геофизических и экологических представлений с помощью разумно подобранных математических функций. Эти функции могут быть при помощи процедур оптимизации достаточно хорошо приближены к наблюдаемой в природе или эксперименте функции в интересующей нас области изменения переменных.

Математическое определение функции отклика следующее. Функцией отклика k-го показателя на воздействие совокупности экологических факторов (xi, Х2, …, х_п) называется функция отображающая экологическое пространство е (хь Х2, …, х_п) на шкалу I^k, которая в каждой точке (xi, Х2, …, х_п)-пространства е сопоставляет число ip^k(x 1, Х2, …, х_п) на шкале /*, т. е. <�р^к: е —? 1^к.

Частной функцией отклика показателя или процесса называют функцию зависимости значений этот показателя от одного экологического фактора, т. е. функцию одной переменной fj (xj). Примеры частных функций отклика скорости роста растения на изменение внешних факторов приведены па рис. 1.2.

Обобщенной функцией F^k называется функция зависимости значений k-го показателя или процесса от всех рассматриваемых факторов, представленная как комбинация частных функций отклика. В зависимости от постановки задачи в качестве обобщенной функции отклика может выступать суммарная биомасса экосистемы или отдельного вида, урожай или такие обобщенные характеристики, как функция (индекс) благополучия системы, функция резистентности, функция модификации и др.

Рис. 1.2. Вид частных функций отклика скорости развития растения сои в период между всходами и бутонизацией: Т — максимальная суточная температура воздуха (град. С); t — минимальная суточная температура воздуха; W — влажность почвы, L — продолжительность светового дня (час) (Малкина-Пых, 1997).

клика:

Наиболее часто используемые на практике частные функции от.

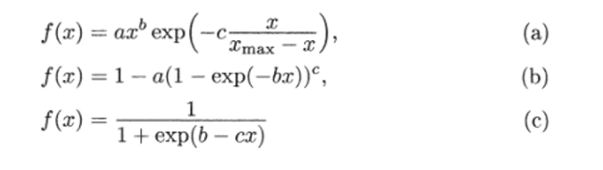
и их модификации. Здесь а, 6, с, ?_тах — параметры, подлежащие идентификации.

Формирование обобщенной функции отклика представляет собой наиболее сложную задачу. Обычно используют мультипликативное представление, позволяющее очертить в многомерном пространстве факторов границу толерантности системы:

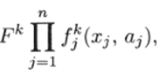
где fj (Xj, Qj) — частные функции отклика; a, j — вектор параметров, подлежащих идентификации; п — количество рассматриваемых факторов.

Задача идентификации обобщенной функции отклика является задачей нелинейной регрессии с достаточно большим количеством параметров идентификации. Задача не может быть упрощена путем снижения ее размерности за счет выделения отдельных частных функций отклика или путем линейной аппроксимации, так как эти процедуры неправомерны в силу сложности системы и неоднозначности связей ее компонентов.

В отличие от классических моделей популяционной динамики и гидродинамики параметры функции отклика не имеют физического или биологического смысла, однако их сочетания, определяющие положение кардинальных точек (например, максимумов) частных функций отклика, могут иметь конкретный биологический смысл и называются параметрами связи. Они также используются при решении задачи идентификации. При решении задачи идентификации параметров в качестве начальных приближений можно использовать экспериментальные данные по отдельным процессам (частным функциям отклика).

Аппарат функций отклика успешно применялся для решения проблем, связанных с анализом отклика лесных экосистем на изменения окружающей среды (Teller et al., 1992), изучения проблем риска (Hubert, 1996). Разработка теорий функций отклика и применение для широкого круга задач экологической экспертизы и формирования индексов качества окружающей среды представлены в работах И. Г. Малкиной-Пых и Ю. А. Пых (1997; 1998). В этих работах также решаются практические задачи прогнозирования продуктивности сортов сельскохозяйственных культур, оптимизации режимов орошения и внесения удобрений, прогнозирования последствий загрязнения территории радионуклидами, предсказания самоочищения звеньев экосистемы от различных поступивших загрязнителей, в том числе пестицидов, прогнозирования динамики органического вещества почв при их использовании для производства сельскохозяйственной продукции и др.