Независимость аксиом ИВ

Свойство независимости аксиом формальной системы означаег, что никакую из аксиом нельзя вывести из других. Для выбранной нами формальной системы ИВ это свойство выполняется.

Если говорить более строго, то свойство независимости можно сформулировать так. Рассмотрим формальную систему ИВ 3, которая отличается от рассмотренной нами формальной системы ИВ тем, что в ней есть только схемы аксиом (А1) и (А2). Независимость третьей схемы аксиом означаег, что в ИВ 3 не выводится формула.

Аналогично формулируются и два других свойства независимости.

Доказательства независимости будут опираться на общий метод, который часто применяется для доказательства независимости аксиом. Основная идея состоит в том, чтобы найти некоторую модель (или интерпретацию), для которой верна данная аксиоматика, и в дайной модели найти какойлибо инвариант, присущий всем аксиомам, кроме испытуемой. Далее проверяется, что правила вывода не изменяют значения инварианта, а отсюда, как следствие, имеем, что интересующую нас аксиому нельзя вывести из остальных. Таким образом, к примеру, и была доказана независимость V постулата Евклида (аксиомы о параллельных прямых) от остальных аксиом геометрии.

В случае исчисления высказываний мы будем строить модели, используя функции, которые зависят от переменных, принимающих значения в некотором множестве М, и принимают значения в том же множестве М. Если заданы функции f-(x) и /_>(#, у), соответствующие отрицанию и импликации, то для каждой формулы ИВ определим функцию, которая реализуется этой формулой, так же, как это было сделано в разделе 1.2: переменной соответствует функция [xi]: Xj Xi если формула А имеет вид ~В, то [А] = f-([B]); а если А = ?->(7, то [А] = /_"([?], [С]). Мы здесь используем обозначение [А] для функции, реализуемой формулой А.

Теорема 1.38. Третья аксиома не зависит от первых двух.

Доказательство. Зададим модель булевыми функциями f-](x) = х, /_Дж, у) = (ж—>у). Функции, которые получаются из первых двух схем аксиом подстановкой вместо отрицания и импликации функций f- и являются тавтологиями (тождественно равны 1). Действительно, в эти аксиомы отрицание вообще не входит, а /_> совпадает с импликацией. Поэтому можно утверждать, что в формальной системе ИВ 3 выводимы только тавтологии.

Теперь подставим функции f- и /_+ в формулу (АЗ), соответствующую третьей аксиоме:

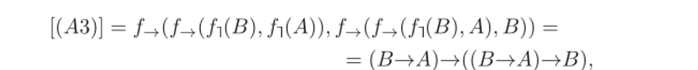
где в последней формуле использована стандартная интерпретация формул ИВ. Вычисление.

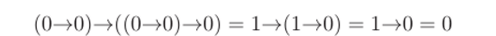
показывает, что эта функция не является тавтологией. Значит, формула (АЗ) невыводима в системе ИВ 3. ?

Теорема 1.39. Первая аксиома не зависит от второй и третьей.

Доказательство. Построим модель с множеством значений {О, О⁷, 1}. Такие странные обозначения объясняются выбором функций /|, /_д при ограничении на множество {0,1}.

они принимают те же значения, что и обычные булевы отрицание и импликация (см. таблицу 1.1).

Проверим, что формула (А2).

(вторая схема аксиом) реализует в такой модели функцию, тождественно равную 1. Значение f->(x, y) никогда не равно 0', поэтому значение формулы (А2) в данной модели отлично от 1 только в том случае, когда [x—>(y—tz)] = 1, а [(x—>y)—>(x—>z)] = 0. Применяя ко второму равенству то же самое рассуждение, получаем условия:

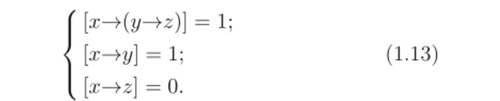
Если х = 1, то из второго условия в (1.13) получаем у = 1, а из первого [у—>z] = [1 —>z] = 1, что противоречит третьему условию. Если х = (У, то из второго условия у = 1, но тогда из третьего условия z ф 1. Значит, [y->z] ф 1,.

[х—>(у->z) = 0, а это противоречит первому условию. Случай х = 0 противоречит третьему условию. Несовместность условий (1.13) показывает, что значение функции, реализуемой формулой (А2) тождественно равно 1.

Проверим то же свойство для формулы (АЗ).

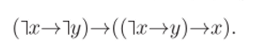
Аналогично предыдущему рассуждению убеждаемся, что если значение формулы (АЗ) не равно 1, то х ф 1, а [~]х] = 1. Но /_Дж, 0) = /_>(х, 0') при любом х, поэтому формула (АЗ) в этом случае принимает такие же значения, как и булева функция в стандартной модели (и, значит, равна 1).

Кроме того, из таблицы 1.1 легко видеть, что если х = 1 и f^(x, y) = 1, то у = 1. Значит, применение правила вывода сохраняет формулы, реализующие тождественно равные 1 функции.

Поэтому из аксиом (А2) и (АЗ) можно вывести лишь формулы, реализующие тождественно равные 1 функции. Для завершения доказательства заметим, что.

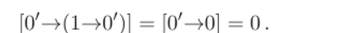
Поэтому формула (х—>(у—>х)) реализует функцию, которая не равна 1 тождественно ?

Теорема 1.40. Втощя аксиома не зависит от первой и третьей.

Доказательство. Здесь мы выберем множеством значений функций {0,1,2}, а функции f-(x) и /_"(#, у) зададим таблицей 1.2.

Докажем, что формула х—>(у—>х) (первая схема аксиом) реализует функцию, тождественно равную 0. Из таблицы 1.2 видно, что /_>. принимает отличное от 0 значение на трёх наборах переменных (0,1), (0,2) и (1,1). Но из таблицы.

видно, что если х = 0, то [у—>х] = [у—>0] = 0; а если х = 1, то [у—>х] = [у—" 1] Ф 1.

Аналогичным образом проверим, что формула.

• (третья схема аксиом) также реализует функцию, тождественно равную 0. Рассмотрим возможные варианты, когда внешняя импликация даёт отличное от 0 значение.
• • Случай (1,1): [1х—>1у] = 1 влечёт [la:] = 0, [1 у] = 2, но последнее равенство невозможно.
• • Случай (0,1): если [(По:—>а/)—= 1, [1т—>1у] = 0, то * = 2, [1т] = 1, [1 х->у = [1—>у] = 0, [1 х-Лу] = [1—>1 у] = = 0. Из последнего равенства заключаем, что [1у] = 0, у = 1. Пришли к противоречию, так как [1—"1] ф 0.
• • Случай (0,2): если [(1т—"у)—i>х] = 2, то х = 1, а [1 х—>у] принимает значения 0 или 1. Значит, [1т—>у) = [0—"у], а у принимает значения 0 или 2. Поэтому [1 у] = 1. Но тогда [1т—>1 у] = [0—> 1] = 2 ф0.

Кроме того, из таблицы легко видеть, что если х = 0 и /-> (я, у) = 0, то у = 0. Значит, применение правила вывода сохраняет формулы, реализующие тождественно равные 0 функции.

Поэтому из аксиом (А1) и (АЗ) можно вывести лишь такие формулы, которые задают функции, тождественно равные 0.

Проверим, что соответствующая второй схеме аксиом формула (х—>(у—>z))—>{(х—>у)—>(x—>z)) реализует функцию, которая не равна 0 тождественно:

Независимость второй схемы аксиом доказана. ?