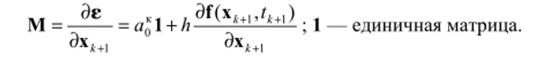О других методах

Среди численных методов интегрирования дифференциальных уравнений выделяют:

=> одношаговые методы, в которых значение x*+i искомой функции на очередном шаге (в момент /*+i) вычисляется на основе значения лд на предыдущем шаге;

=> многошаговые методы, в которых jc*+i вычисляется по значениям, найденным на нескольких предыдущих шагах.

Од пошаговые методы базируются на разложении искомого решения в окрестности точки в ряд Тейлора и использовании формул численного дифференцирования для вычисления производных в нескольких промежуточных точках шага. К ним относятся явные алгоритмы Рунго — Кутта, простейшим из которых является рассмотренный выше алгоритм Эйлера. В алгоритмах Рунге — Кутта вычисления производных заменяются вычислениями значений функции в нескольких промежуточных точках шага. Алгоритм четвертого порядка можно представить в следующем виде.

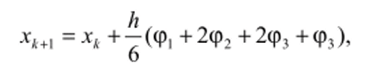
где (р, — угловые коэффициенты касательных в различных точках: ф] — в начальной точке **, /* шага; ф2, Фз — в середине шага; фд — в конце шага. Коэффициенты ф, вычисляются, но следующим формулам:

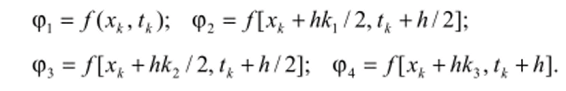
Приведенный алгоритм имеет порядок р = 4, поэтому методическая погрешность невелика (оценивается как Л7г) и вычисления можно проводить с относительно большим шагом.

В многошаговых методах численного интегрирования используется информация о предыдущих точках, полученных в процессе вычисления. К ним относятся методы Адамса — Бэшфорта и Адамса — Мултона.

Явные алгоритмы Адамса — Бэшфорта описываются выражением:

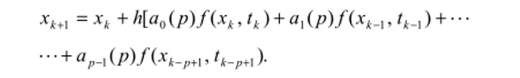
Коэффициенты а"(п = 0, 1,…, р -1) зависят от порядкар и определяются из решения соответствующей системы уравнений. Значение р = 1 соответствует явному алгоритму Эйлера (6), а р = 3 — трехшаговому алгоритму третьего порядка:

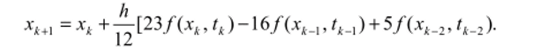
Для начала вычислений необходимо располагать значениями функций в р = 3 предыдущих точках.

Неявные алгоритмы Адамса — Мултона вычисляются по формуле:

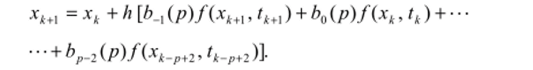
Значения р = 1 соответствует неявному алгоритму Эйлера, р = 2 — алгоритму трапеций, а р = 3 — более точному двухшаговому алгоритму Адамса — Мултона третьего порядка:

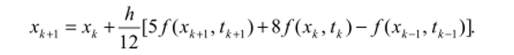
Достоинство многошаговых алгоритмов проявляется в возможности более легкого контроля над распространением ошибки, а также в большей эффективности, поскольку функция вычисляется в двух точках, а не в четырех, как в алгоритме Рунге — Кутта.

Формулы дифференцирования назад. Линейные многошаговые формулы, используемые при численном интегрировании дифференциальных уравнений, получаются путем:

=> аппроксимации искомой функции интерполяционным полиномом;

=> выбора коэффициентов полинома таким образом, чтобы его значения совпадали с найденными на предыдущих шагах значениями решения и его производной.

Многошаговые формулы строятся по известным значениям **+!-*>, */Н2-Р> ->*А+Ь функции л (/) и производных х’м-р, х’ь-2-р,…"**+ь Ах’ы в МО;

менты tk*-p, tk2 fn …"/д+i" /*+|. Случай /1=0 приводит к формуле, которая называегся прогнозом (предсказанием), а случай А — 1 — к формуле коррекции.

Формулы дифференцирования назад (ФДН), или обратного дифференцирования, не требуют знания производных в предшествующие моменты времени. В их основе лежит представление производной х*+1 искомой функции x (t) в точке /*+1 через значение л*+1 и известные значения в р предшествующих точках х_к, х_к", …, (/^-предысторию). Формулы дифференцирования назад для прогноза и коррекции имеют вид.

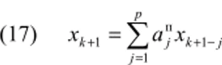
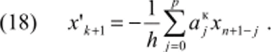
В явную формулу прогноза (17) входят только известные из предыдущих шагов значения х_к-и •••" **+i-р функции х (/). Она позволяет определить начальное значение jc*+i для коррекции. Неявная формула (18) коррекции после подстановки се в исходное дифференциальное уравнение х' =J[x, t) позволяет итерационным методом получить более точное значение лг*+/* где /— номер итерации. Таким образом, получив один раз прогнозируемое значение переменной ее значение путем итераций уточняется, но формуле коррекции.

Метод численного интегрирования с использованием ФДН (17), (18) называется методом р-го порядка. Построенные на его основе алгоритмы устойчивы, позволяют изменять нс только шаг, но и порядок, обеспечивают предельную для линейных многошаговых методов точность расчета.

В основе вывода ФДН лежит представление точного решения x (t) на интервале t_k+i-_P- /*н в виде полинома р-й степени P (t) = (Xq+ a +…+СС_pt^p, проходящею через р + 1 точку «х/^i- С помощью полинома можно построить систему линейных алгебраических уравнения для определения коэффициентов я,-ФДН.

Покажем использование ФДН для решения системы дифференциальных уравнений.

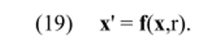
полагая, что входящие в (17), (18) величины являются векторами x*+i-p" х*+2-#">—" Х*-Ь ^хк и их значения известны.

Подставим (18) в (19) и перепишем в виде.

На данном шаге сумма известна в (20) и может быть представлена вектооом г. Тогда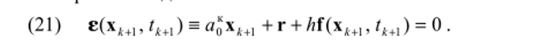

Итерации можно выполнить по методу Ньютона — Рафсона: 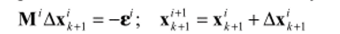где верхний индекс обозначает номер итерации; М — якобиан уравнения (21);