Связь ожидаемой полезности с отношением к риску

Вопрос об ожидаемой полезности возникает в ситуации, когда речь идет о принятии решений в условиях риска. Как уже было отмечено ранее, выбор ЛПР, а следовательно, его функция полезности зависят от информации, которой он владеет, а также от его вкусов и предпочтений. Далее будет исследовано, как отношение ЛПР к риску влияет на вид его функции полезности.

Ранее были отмечены некоторые трудности, связанные с понятием полезности денежного дохода г и ее измерения. Возможность рассматривать такие доходы и соответствующие им функции полезности возникает в ситуации, когда действие других факторов является столь незначительным, что им можно пренебречь. Далее речь пойдет именно о таких доходах и полезностях.

Выпуклые функции полезности.

Определение

Говорят, что вещественная функция g, определенная на интервале (а, Ь) вещественной прямой, выпукла на (я, Ь), если для любых двух точек х и у из (а, Ь) и любого числа а, такого, что 0.

Геометрически соотношение (14.10) означает, что отрезок прямой, соединяющей любые две точки кривой у = g (x), нигде между этими двумя точками не лежит ниже кривой.

Функция g называется строго выпуклой на (я, Ь), если в (14.10) имеет место строгое неравенство для всех нар различных точек х и у из (а, Ь). Геометрически это означает, что функция g выпукла и кривая у = g (x) не содержит линейных кусков. Примеры графиков выпуклых функций представлены на рис. 14.1.

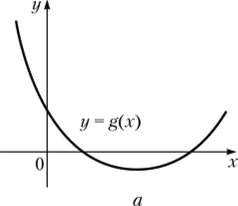
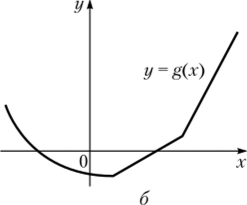
Рис. 14.1. Строго выпуклая функция g (я); выпуклая функция g, не являющаяся строго выпуклой (б).

Основной результат, известный как неравенство Йенсена, представлен в виде следующей теоремы. Данное неравенство относится к математическим ожиданиям выпуклых функций и верно независимо от того, конечен или бесконечен интервал (а, Ь), на котором задана выпуклая функция. Если интервал конечен, то он может быть как открытым, так и замкнутым в своем конце.

Теорема (неравенство Йенсена)

Пусть g — выпуклая функция на интервале (а, Ь) и — случайная величина, такая, что Р{^ е (a, b)} = 1 и существуют средние Е% и Eg (^). Тогда E (_g(X)) >gm.

Если функция g строго выпукла и Р{^ = E (q) ^ 1}, то имеет место строгое неравенство.

Рассмотрим теперь ситуацию, в которой множество R доходов является интервалом (а, б) денежных выигрышей г и функция полезности ?/данного индивидуума (ЛПР) строго выпукла на (а, Ь). Из неравенства Йенсена следует, что тогда этот индивидуум предпочтет игру со случайным выигрышем ?, из интервала (а, !/) игре с заведомым выигрышем В частности, если интервал (а, Ь) содержит точку 0, то игру с нулевым средним он предпочтет тому, чтобы вообще не играть.

Обратите внимание!

По этим причинам можно называть лиц со строго выпуклой функцией полезности «любителями риска» или «ищущими риск» (от англ, risk loving, risk seeking).

Понятно, что два любителя риска будут заключать пари с равными ставками относительно того, выпадет герб или решетка, поскольку они оба предпочитают играть, нежели смотреть.

Обратите внимание!

В случае нестрогой выпуклости функции полезности ее линейная часть соответствует нейтральности игрока к риску (от англ, risk neutral).