Управляемость линейных стационарных объектов

Пусть уравнение (1.12).

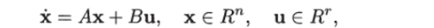
описывает стационарную систему, т. е. матрицы А и В являются постоянными. Введем в рассмотрение матрицу.

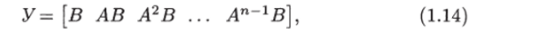
столбцы которой представляют собой столбцы матрицы В и произведений матриц ЛВ, Л²В, …, А^п~¹В. Эту матрицу называют матрицей управляемости.

Критерий управляемости линейных стационарных систем.

Линейный стационарный объект вполне управляем тогда и только тогда, когда матрица управляемости имеет максимальный ранг, т. е. когда ее ранг равен п.

Напомним, что ранг матрицы равен числу независимых строк, числу независимых столбцов и порядку отличного от нуля минора максимальной размерности.

Определение 1.2. Пару (А, В) называют управляемой или вполне управляемой, если ранг матрицы управляемости (1.14) равен п.

Ниже при доказательстве критерия управляемости используется теорема Кэли-Гамильтона, которая формулируется следующим образом [32]:

любая (п х п) -матрица удовлетворяет своему характеристическому уравнению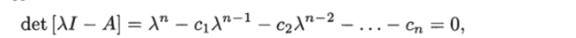

т. е. справедливо равенство

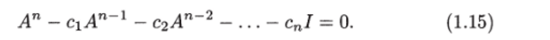
Доказательство критерия управляемости. В силу утверждения 1.1 достаточно ограничиться случаем, когда х (0) = х° = = 0. Решение уравнения (1.12) при постоянных матрицах А и В и начальном условии х (0) = х° = 0 имеет вид (см. (1.10)).

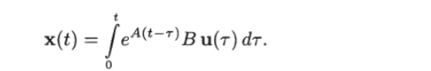
Отсюда, положив t = tf и x (tf) = х-^, получим.

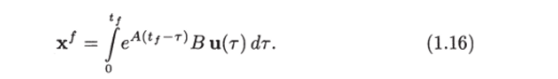
Необходимость. Из определения матричной экспоненты имеем 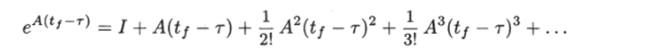Подставив это выражение в равенство (1.16), получим.

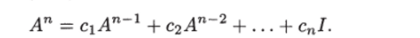aside class="viderzhka__img" itemscope itemtype="http://schema.org/ImageObject">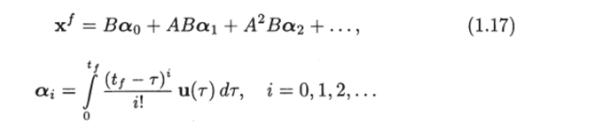

Из равенства (1.15) получаем где Умножив обе части этого равенства справа на матрицу В, получим.

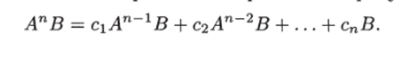
Умножив обе части последнего равенства слева на А и подставив справа вместо А^пВ его выражение из последнего равенства, найдем.

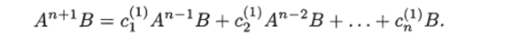
Далее, продолжая аналогичные операции над получаемыми соотношениями, будем иметь.

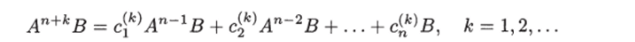
Используя эти соотношения, можно исключить из (1.17) все А¹ В с / Следовательно, конечное значение x (tf) = х* может быть представлено в виде линейной комбинации столбцов матрицы управляемости, и точка, определяемая этим значением, при любом кусочно непрерывном управлении будет принадлежать пространству, порождаемому столбцами матрицы управляемости. Поэтому если ранг матрицы управляемости меньше п, то будет существовать подпространство, в которое нельзя будет перевести объект.

Достаточность. Объект будет вполне управляем, если уравнение (1.16) относительно неизвестного управления имеет решение при любом хЛ Решение будем искать в виде [15].

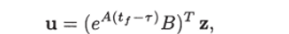
где z — вектор из Rⁿ. Подставив это выражение для управления в уравнение (1.16), получим.

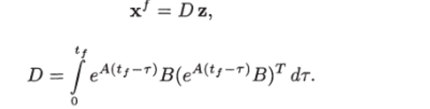
где Таким образом, вопрос о существовании решения интегрального уравнения свелся к вопросу о существовании решения алгебраического уравнения. Полученное алгебраическое уравнение имеет решение при любом х*^, если detD^O. Следовательно, достаточно показать, что выполняется это неравенство. Допустим, что это не так: det D = 0. Тогда соответствующее однородное уравнение имеет ненулевое решение, т. е. существует вектор z ф 0 такой, что D z = 0. Умножив это равенство слева на т? и подставив выражение для ?>, получим.

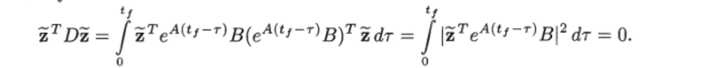
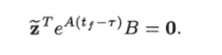
В силу непрерывности подынтегрального выражения последнее равенство возможно, если на всем интервале 0 ^ т ^ tf выполняется равенство Дифференцируя это тождество по т, получим соотношения.

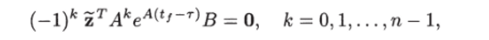
откуда при г = tj находим.

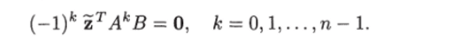
Заметим, что А⁰ = /. Из последних равенств следует, что ненулевой вектор z из Rⁿ ортогонален всем векторам-столбцам матрицы управляемости, что невозможно, так как ранг матрицы управляемости равен п. Следовательно, допущение, что det D = 0, неверно. Критерий управляемости полностью доказан.

Пример 1.2. Определить, при каких значениях параметра а объект, заданный уравнениями вполне управляем.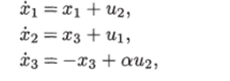

Решение. Матрицы А и В в данном случае имеют вид.

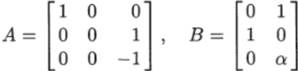
Найдем произведения матриц АВ и А²В:

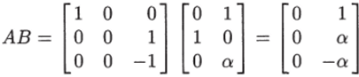
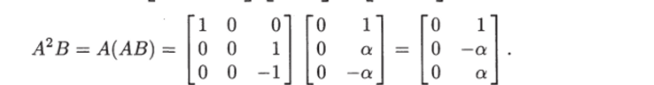
Для матрицы управляемости имеем.

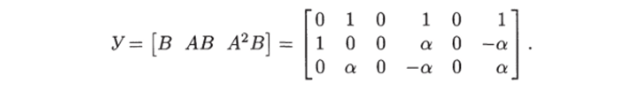
Минор, составленный из первого, второго и четвертого столбцов, имеет вид.

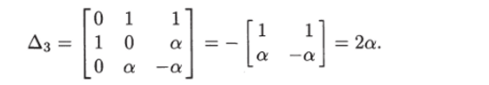
Он отличен от нуля при а ф 0. При а = 0 все элементы последней строки матрицы управляемости обращаются в нуль, и ранг матрицы управляемости не может быть больше 2. Поэтому рассматриваемый объект вполне управляем при а ф 0.

Утверждение 1.2. Одномерная управляемая система, описываемая уравнением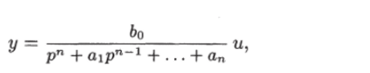

где 6о Ф 0, вполне управляема.

Доказательство. Как было показано в параграфе 1.2, если преобразовать последнее уравнение в нормальную форму, то уравнение состояния примет вид.

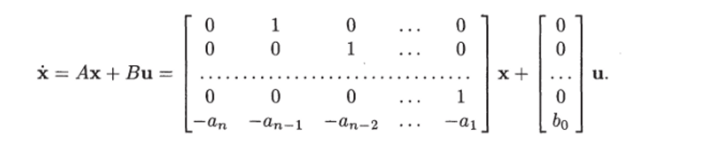
Вычислим произведения матриц, необходимые для получения матрицы управляемости:

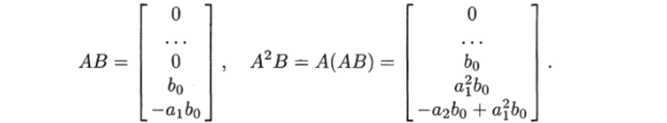
Продолжая вычисления, нетрудно заметить, что в произведении Л^кВ (к < п — 1) в (к + 1)-й строке снизу стоит &о, выше — одни нули и в произведении А^п~¹В в первой строке (сверху) стоит &оПоэтому в матрице управляемости на неглавной диагонали будут стоять одни &о, левее этой диагонали — одни нули. Следовательно, детерминант матрицы управляемости будет отличен от нуля, и управляемая система вполне управляема.

Инвариантность свойства управляемости к линейным преобразованиям.

Свойство управляемости при неособом линейном преобразовании не меняется. Действительно, рассмотрим неособое линейное преобразование.

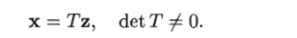
При таком преобразовании уравнение (1.12) принимает вид.

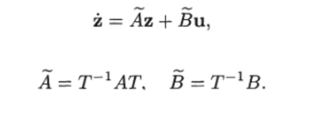
где Убедимся, что пара (А, В) вполне управляема. Для матрицы управляемости этой пары имеем.

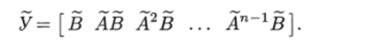
Как нетрудно убедиться,.

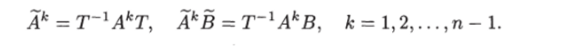
Подставив эти выражения в последнее соотношение, получим.

Так как матрица Т^-1 неособая и ее ранг равен п, то ранг матрицы управляемости У «преобразованного объекта» равен рангу матрицы управляемости У исходного объекта.