Метод функций ляпунова

Основы общей теории устойчивости были заложены А. М. Ляпуновым в его книге «Общая задача об устойчивости движения», которая вышла в 1892 г. В этой книге им был предложен общий метод исследования устойчивости движения, который называется вторым или прямым методом Ляпунова. Этот метод основан на построении специальной функции, которая получила название функции Ляпунова. Прямой метод Ляпунова получил дальнейшее развитие в трудах российских и зарубежных авторов. Метод исследований, основанный на построении функции Ляпунова, включая прямой метод Ляпунова, стали называть методом функций Ляпунова.

Знакопостоянные и знакоопределенные функции

В большинстве случаев функции Ляпунова являются знакоопределенными, а их производные — знакоопределенными или знакопостоянными функциями. Познакомимся с этими функциями.

Определение знакопостоянных и знакоопределенных функций.

Рассмотрим функцию V (x), определенную в некоторой области D С Rⁿ и функцию Г (х, ?), определенную на прямом произведении D х [0, оо), т. е. при х € D и 0 ^ < оо. Область D содержит начало координат: 0 € D. Функции V(х) и V(х, ?) являются непрерывными и обладают непрерывными производными по всем своим аргументам.

Функция У (х) называется знакоположительной или положительно полуопределенной в области D, если Г (0) = 0 и V (x)^0 всюду на D, и называется знакоотрицательной или отрицательно полуопределенной в области D, если Г (0) = 0 и Г (х) ^ 0 всюду на D.

Функция V{x, t) называется знакоположительной или положительно полуопределенной в области D, если при всех t ^ to (?о ^ 0) V(0, t) = 0 и V(х, t) ^ 0 всюду на D, и знакоотрицательной или отрицательно полуопределенной в области D, если при всех t ^ to (to ^ 0) Г (0, t) = 0 и V(х, t) ^ 0 всюду на D.

Знакоположительные и знакоотрицательные функции в области D называются знакопостоянными функциями области D.

Функция V'(x) называется положительно определенной в области если К (0) = 0 и V (x) > 0 всюду на D, кроме точки х = О, и называется отрицательно определенной в области D, если У (0) = 0 и К (х) < 0 всюду на D, кроме точки х = 0.

Функция V(х, t) называется положительно определенной в области D, если при всех t ^ to (to ^ 0) V (0, t) = 0 и найдется такая положительно определенная в области D функция V⁺(x), что при всех t ^ ^ to V (x, t) > К⁺(х) всюду на D, кроме точки х = 0, и называется отрицательно определенной в области D, еслиК (х, t) является положительно определенной в области D.

Положительно определенные и отрицательно определенные функции в области D называются знакоопределенными функциями в области D. Очевидно, знакоопределенные функции являются частным случаем знакопостоянных функций.

Функции, которые не являются знакопостоянными функциями в области D, называются знакопеременными функциями в области D.

В качестве примера рассмотрим следующие функции:

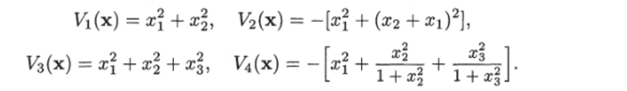
Среди этих функций в пространстве R³ функция Vi (x) является положительно полуопределенной, функция У^(х) «отрицательно полуопределенной, функция Уз (х) — положительно определенной и функция V^x) — отрицательно определенной. Функции Ц (х) и V^(x) являются знакопостоянными, а функции Уз (х) и V^(x) ^— знакоопределенными. В пространстве R² функция Vi (x) является положительно определенной, а функция V^x) — отрицательно определенной.

Если К (х) является знакоопределенной функцией, то существует такое положительное число rj, что все поверхности К (х) = с, где |с| < < 77, являются замкнутыми относительно точки х = 0 поверхностями; если V (x) является знакоопределенной функцией и |V (х) | оо при |х| —" оо, то все поверхности V(х) = с при любом с являются замкнутыми относительно точки х = 0 поверхностями [7].

Покажем на примере, что не при всех знакоопределенных функциях V(х) все поверхности V (x) = с при любом с являются замкнутыми относительно точки х = 0 поверхностями. В качестве примера рассмотрим в пространстве R² положительно определенную функцию вид.

В этом случае при с = г² уравнение поверхности V(х) = с принимает.