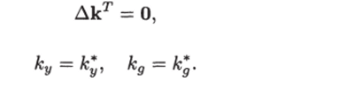Алгоритмы адаптивного управления с ЭМ

Задачу синтеза адаптивной системы управления с ЭМ содержательно можно сформулировать следующим образом. Заданы уравнения объекта и эталонной модели. Требуется синтезировать алгоритм адаптивного управления, т. е. алгоритм управления (основного контура) и алгоритм адаптации, при которых система глобально устойчива и ошибка слежения — разность между выходными сигналами основного контура и эталонной модели — сходится к нулю при стремлении времени к бесконечности.

Здесь предполагается, что эталонная модель задана, хотя она должна быть определена исходя из заданных требований к синтезируемой системе управления. Это связано с тем, что определение эталонной модели по заданным требованиям к системе управления является обычной задачей управления и не связано со спецификой адаптивного управления.

Алгоритм адаптивного управления линейным объектом 1-го порядка.

Начнем изучение метода синтеза адаптивных систем управления с ЭМ со случая, когда объект описывается линейным уравнением 1-го порядка.

Здесь у — выход, и — вход (управление), ао, &о ^— неизвестные параметры, знак параметра &о известен.

Пусть на основании заданных требований к синтезируемой системе выбрана эталонная модель, которая описывается уравнением.

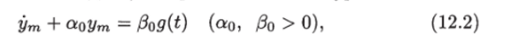
где Ут — выход эталонной модели, g (t) — задающее воздействие, которое предполагается ограниченным.

Требуется найти алгоритм адаптивного управления, при котором ошибка слежения стремится к нулю при t —> оо:

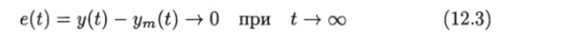
и система глобально устойчива.

Утверждение 12.1. Алгоритмом адаптивного управления с ЭМ (12.2) объектом (12.1), обеспечивающим глобальную устойчивость и выполнение целевого условия (12.3), является алгоритм управления

совместно с алгоритмом адаптации

где ky_f k_g — варьируемые параметры, 7 — произвольная положительная константа.

Доказательство. Как отмечалось, при адаптивном управлении с ЭМ одним из основных требований является возможность принятия варьируемыми параметрами регулятора идеальных значений, т. е. таких значений, при которых уравнение основного контура совпадает с уравнением эталонной модели. Покажем, что алгоритм (12.4а) удовлетворяет этому условию.

Подставив выражение для управления (12.4а) в уравнение объекта (12.1), получим уравнение основного контура.

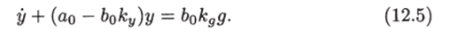
Это уравнение совпадает с уравнением эталонной модели (12.2), когда.

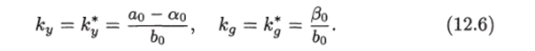
Дальше, чтобы можно было использовать метод функций Ляпунова, преобразуем уравнения синтезированной системы управления в уравнения в отклонениях — переменных е, А/с_у, ДА^, где.

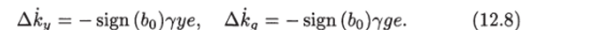
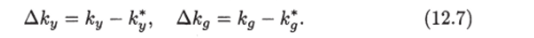
Так как к* и к* являются константами, алгоритм адаптации (12.46) можно записать в виде Для получения уравнения для переменной е вычтем из уравнения основного контура (12.5) уравнение эталонной модели (12.2):

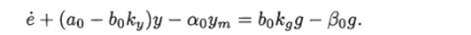
Прибавив и вычитая из левой части аоу, получим.

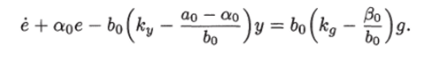
Итак, адаптивная система управления в новых переменных описывается уравнениями (12.8) и (12.9).

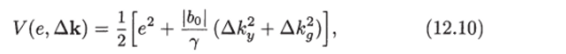
где Дк = {Ак_у Ак_д)^т. Производная от этой функции по времени имеет вид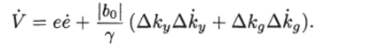

Учитывая обозначения (12.6) и (12.7), последнее уравнение можно представить в виде.

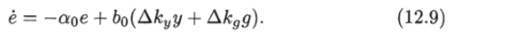
В качестве кандидата на функцию Ляпунова рассмотрим квадратичную форму Подставив в правую часть выражения для производных из уравнений адаптивной системы управления (12.8) и (12.9), получим.

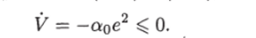
Таким образом, квадратичная форма (12.10) является функцией Ляпунова для синтезированной системы, и эта система устойчива по Ляпунову. Так как V (e, Дк) > 0 (положительно определена) и V ^ 0, функция V (e, Дк) и соответственно переменные е, Ак_у(к_у) и Ак_д(к_д) (см. (12.10)) являются ограниченными. Кроме того, квадратичная форма К (е, Дк) как функция времени стремится к конечному пределу при t оо.

Так как по условию задачи задающее воздействие g (t) ограничено, то, как следует из (12.9), производная ё и соответственно вторая производная V = 2аоеё ограничены. Следовательно, первая производная V равномерно непрерывна, по лемме Барбалата V —> 0 и, как следствие, e (t) —> 0 при t -> оо.

Из приведенного анализа следует, что ограниченность переменных и сходимость ошибки слежения e (t) к нулю гарантируется при любых положительных 7, а₀ и 0q.

При адаптивном управлении с ЭМ основное целевое условие — это обеспечение сходимости к нулю ошибки слежения e (t) = y (t) — ym (t). Если параметры регулятора принимают идеальные значения, то, естественно, это условие будет выполнено. Однако, как покажем ниже, из сходимости к нулю ошибки слежения не следует параметрическая сходимость — сходимость варьируемых параметров к идеальным значениям.

Параметрическая сходимость зависит от структуры задающего воздействия. Если задающее воздействие простое, например константа, то по окончании процесса адаптации варьируемые параметры в зависимости от начальных условий могут принять различные значения. Проанализируем этот вопрос на примере рассмотренной выше адаптивной системы управления.

Как было показано, ошибка слежения е (?)0 стремится к нулю при t оо. Следовательно, можно принять, что при достаточно большом времени e (t) = 0 и e (t) = 0. Тогда из уравнения (12.9) следует.

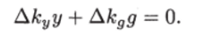
Если задающее воздействие является константой (g (t) = до), то по окончании переходного процесса, т. е. при достаточно больших значениях t (см. (12.2)),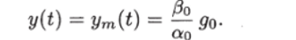

Подставив это выражение в предыдущее равенство, получим.

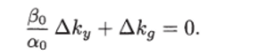
Отсюда видно, что параметры регулятора сходятся не к определенной точке, а к любой точке прямой. Однако когда задающее воздействие g (t) обладает таким свойством, что вектор сигналов v = (у д)^т удовлетворяет так называемому условию постоянного возбуждения, сходимость к нулю ошибки слежения влечет за собой параметрическую сходимость [69].

Определение 12.1. Условие постоянного возбуждения п-векторного сигнала v (t) выполняется, если существуют положительные константы Т и, а такие, что при любом t > 0.

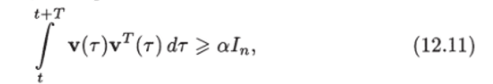
где 1_п — единичная матрица порядка п.

Покажем, что в случае адаптивной системы с объектом 1-го порядка, которую мы рассмотрели, при выполнении условия (12.11) имеется параметрическая сходимость.

Используя векторные обозначения Дк = (Ak_y Ак_д)^т и v = = (у д)^т, уравнение, которое получается из (12.9) при e (t) = e (t) = = 0, можно записать в виде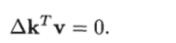

Умножив последнее равенство справа на ^т и проинтегрировав от t до t + T, получим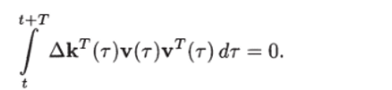

По окончании процесса адаптации, т. е. при достаточно большом t, вектор Дк становится постоянным, и его можно вывести за знак интеграла: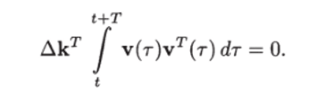

или Отсюда следует, что если выполняется условие постоянного возбуждения сигнала (12.11), то.