Б теория точечных оценок

Несмещенные оценки с минимальной дисперсией

Предположим, что о распределении случайной величины X известно, что оно принадлежит некоторому параметрическому семейству распределений. Для непрерывной случайной величины это означает, что известен вид плотности /?(л: 10), но неизвестно значение параметра 0, определяющего конкретную плотность. Параметр 0 может быть вектором. Например, для нормального распределения 0 = (р, ст)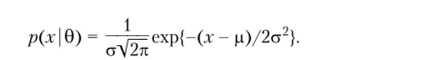

Для дискретной случайной величины р (х | 0) будет обозначать вероятность Р (Х = .г). Например, для пуассоновского распределения.

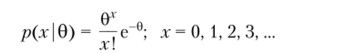
Пусть т (0) — некоторый числовой параметр, представляющий для нас интерес. Например, т (0) = 0, т (р, а) = р, т (р, а) = р/а.

Рассмотрим задачу оценивания, состоящую в построении такой функции t = (х₍, …, х_п), чтобы при подстановке вместо аргументов х_х,…, х" данных выборки получены числа, близкие к т (0). Такую близость можно обеспечить лишь в среднем. Поэтому требования, предъявляемые к качеству оценок, формулируется в вероятностных терминах, относящихся к распределению оценок, рассматриваемых как случайные величины. Это требование, состоящее в том, чтобы значения оценки в большинстве опытов были близки к значению оцениваемого параметра, можно сформулировать в виде следующего определения.

Определение. Оценка t = (x_h …, х_п) называется несмещенной для т (0), если …, х") = т (0) для всех 0, где М_е ;

символ математического ожидания при условии, что случайный вектор (рс, …, х_п) имеет распределение L (x |0) = = р (х₁|6)…р (х"|0). _ _.

Например, как показанно выше, х и S² — несмещенные оценки для р и а² соответственно.

Как правило, одно лишь требование несмещенности не выделяет оценку t (x) однозначно, поэтому теперь желательно потребовать малость дисперсии этой оценки. Чтобы статистика могла служить хорошей оценкой данного параметра т (0), необходимо, чтобы распределение этой статистики было сосредоточенно в достаточной близости от неизвестного значения т (0) и вероятность больших отклонений этой статистики от т (0) была достаточно мала. Тогда при систематическом многократном применении этой статистики в качестве оценки данной характеристики в среднем будет получаться приемлемая точность. Вероятность больших отклонений будет мала, и они будут встречаться редко. Таким образом, среди всех несмещенных оценок t (x) для т (0) более желательной является та оценка, которая имеет минимальную дисперсию D$(t (x)) = M (t (x) — т (0))² для всех 0.

Такие оценки называются несмещенными оценками с минимальной дисперсией (НОМД).

Определение. Несмещенной оценкой с минимальной дисперсией называется такая оценка t*(x _1?…, х_п)_у что Dt* < Dt для всех 0, для любой несмещенной оценки t (x_{,…, х_п) параметра т (0). Уже эти требования, как правило, выделяют оценку t (x) однозначно, если такая оценка вообще существует. Существование же НОМД имеет место далеко не всегда, так как дисперсия для этих оценок должна быть минимальной равномерно по 0. Это обстоятельство является, пожалуй, самым серьезным аргументом против таких сильных требований.

Определение. Оценка t (pC,…, х_п) называется состоятельной оценкой параметра т (0), если она сходится по вероятности к т (0) при неограниченном увеличении числа наблюдений, т. е.

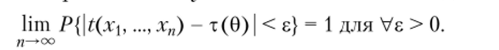
Итак, состоятельность оценки означает, что при достаточно большом количестве наблюдений п со сколь угодно большой достоверностью отклонение оценки от истинного значения параметра меньше любой наперед заданной величины.

Для того чтобы несмещенная оценка была состоятельной, достаточно, чтобы дисперсия оценки стремилась к нулю при п—> °° (это следует из неравенства Чебышева) [11 — 13].

Пример 6.1. Показать что оценки.

являются состоятельными оценками.

Решение. По закону больших чисел.

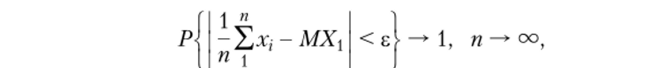
1 Д т. е. оценка а) состоятельна, так как х = - 2^xf,

п х

1 Д т. е. оценка а) состоятельна, так как х = - 2^х{,

п х

Первый член является средним арифметическим случайных величин xf_y следовательно, он сходится по вероятности к Mxf, второй член сходится по вероятности к [Мх]². Это означает, что 5² по вероятности сходится к Mxf — {МхУ = Dxy. Следовательно, оценка является состоятельной, но она не является несмещенной.

Пример 6.2 (существование нескольких несмещенных оценок).

X_t…, х_п — независимые одинаково распределенные случайные величины, имеющие пуассоновское распределение Оценка

является несмещенной оценкой для дисперсии. Из того, что для пуассоновского распределения математическое ожидание и дисперсия равны 0 и х является несмещенной оценкой для 0 следует, что х является несмещенной оценкой для дисперсии 0. Кроме того, любая комбинация ах + (1 — a)5j² является несмещенной оценкой 0 (а е °°), т. е.

Однако оценка х имеет наименьшую дисперсию.

Пример 6.3 (когда не существует несмещенной оценки). Производится одно наблюдениех, где х — случайная величина, имеющая пуассоновское распределение с неизвестным параметром 0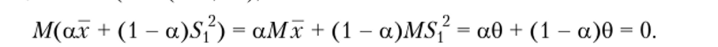

Показать, что для т (0) ⁼ q не существует несмещенной оценки.

Решение. Предположим, что t (x) является несмещенной оценкой т (0), т. е. M_Qt (x) = т (0), откуда.

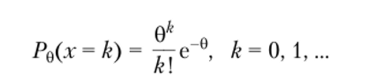
Окончательно.

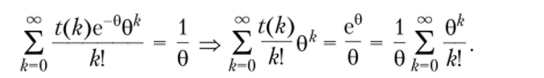
И как легко понять, что не существует функции t (x), для которой последнее равенство было бы справедливо для всех 0 > 0.

Пример 6.4 (когда несмещенная оценка абсурдна). Случайная величина X имеет геометрическое распределение

(число неудач, предшествующих первому успеху в последовательности испытаний Бернулли). Пусть проводится одно наблюдение х. Несмещенной оценкой параметра р является оценка.

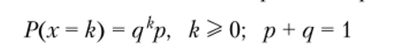
Действительно,.

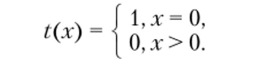
Однако эта оценка абсурдна, так как, например, если первый успех получен на втором испытании, т. е. х = 1, то абсурдно говорить, что вероятность успеха р = 0.