Крутильные колебания. 
Сопротивление материалов с использованием вычислительных комплексов

При крутильных колебаниях роль массы т исполняет момент инерции массы J_nr Уравнение колебательного движения имеет вид.

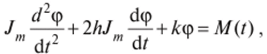
где к — жесткость стержня при кручении. Жесткости при кручении и при изгибе разные.

Решение этого уравнения аналогично решению уравнения (14.1). Соответственно подобным получается и выражение дчя круговой частоты со:

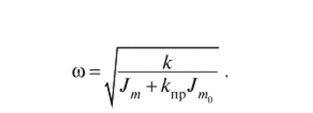
Замечания к расчету собственных частот колебаний

Ранее рассматривалось только определение собственной частоты системы с одной степенью свободы, как правило, для прямых стержней. Для рам и кривых брусьев движение точек в процессе колебаний происходит по сложным криволинейным траекториям и следует учитывать несколько степеней свободы. В этом случае расчет многократно усложняется.

Расчет колебаний систем с большим числом степеней свободы лучше всего производить с использованием метода конечных элементов, как описано в гл. 24. Для различных случаев колебания двух-трех массовых систем готовые формулы для определения собственных частот можно найти в справочниках.

Следует иметь в виду, что при рассмотрении балки как системы с одной степенью свободы она не перестает быть системой с бесконечным числом степеней и с бесконечным количеством собственных частот. На рис. 14.9 приведены формы колебания на первых трех собственных частотах консольной балки.

Рис. 14.9. Формы колебания консольной балки.

Собственные частоты со, и максимальные амплитуды колебаний Aj приведены для линейки из оргстекла длиной 0,5 м. Заметим, что никакой кратности собственных частот не наблюдается. Амплитуда колебаний максимальна для первой (низшей) собственной частоты. Для второй она уже в три раза меньше, для третьей — в 10 раз меньше, чем для первой. Для четвертой собственной частоты амплитуда исчезающе мала. Если дотронуться рукой, можно ощутить дрожание линейки, но померить амплитуду колебаний уже нельзя.

Наибольшие деформации и напряжения в любой системе возникают при резонансе на первой собственной частоте, поэтому для расчета на прочность важно знать именно первую (низшую) собственную частоту. Формулы (14.8) и (14.13) можно использовать и при расчете рам для определения первой собственной частоты. При этом ошибка может быть довольно большой.

Не следует забывать, что расчеты на прочность вообще не отличаются высокой точностью. Какими бы точными не были расчетные формулы, ошибка в определении механических свойств материала и в выборе коэффициента запаса, необходимость учета вероятности разрушения не позволяют достигнуть высокой точности расчета.

Ориентировочно можно определить и первую собственную частоту сложной конструкции. Допустим, перед вами «черный ящик» — сложная конструкция с исполнительным органом-рычагом. Для оценки его собственной частоты определим жесткость конструкции. Подвесим на рычаг любой груз весом F и измерим перемещение Д_стат под действием этого груза. Тогда жесткость к = F/Д_стаг По формуле (14.8) определяем ориентировочную низшую собственную частоту конструкции.

Частота колебаний исполнительного органа при эксплуатации не должна приближаться к собственной частоте колебаний конструкции. Если простейший расчет по формуле (14.8) показывает близость таких частот, надо изменить жесткость системы или ее массу. Иногда достаточно положить на раму мешок с песком, чтобы резко уменьшить собственную частоту конструкции, или приварить какую-нибудь перекладину, чтобы увеличить жесткость и собственную частоту.