Евклидовы кольца. 
Дискретный анализ. 
Основы высшей алгебры

Далее мы будем искать максимальные идеалы в специальных кольцах, которые называются евклидовыми.

По определению, коммутативное кольцо R называется евклидовым, если для пего выполнены следующие свойства.

Е1: Кольцо R — целостное (т. е. в нём нет делителей нуля: из ab = 0 следует, что а = 0 или b = 0).

Е2: Для каждого ненулевого элемента кольца определена числовая характеристика — норма, которая принимает целые неотрицательные значения. Т. е. норма — это такое отображение N: R{0} Z, что N® ^ 0.

ЕЗ: Возможность деления с остатком означает, что для любых элементов а, Ъ кольца, Ъ ф 0, существуют такие q, г, что а = qb + г и либо г = 0, либо N® < N (b). Элемент г называется остатком от деления а на Ь. Это основное свойство нормы. Собственно, отсюда и возник термин «евклидово». Дело в том, что в дошедших до нас рукописях термин «деление с остатком» впервые появляется в сочинениях Евклида.

Е4: Норма произведения двух ненулевых сомножителей больше либо равна норме любого из сомножителей. Формально: для любых a, b € R, а Ф 0, b Ф 0 выполнено N (ab) ^ ^ тах (Л^г(а), N (b)).

Утверждение 2.23. Евклидово кольцо является кольцом с единицей.

Доказательство. Выберем такой ненулевой элемент е^г евклидова кольца R, что N (e') принимает минимально возможное положительное значение (здесь существенно, что значения норм элементов целые неотрицательные, поэтому минимум достигается). Разделим произвольный элемент а на е' с остатком: а = qe' + г. По свойству ЕЗ верно одно из двух: либо N® < < N (e'), либо г = 0. Первое невозможно в силу минимальности нормы е'. Значит, а = qe'. Итак, все элементы кольца кратны е' (делятся без остатка). В частности, это верно и для самого.

ee' = ее'. Но тогда для любого а? R имеем ае' = аее т. е. е'(а — ае) = 0. Поскольку кольцо R целостное и е' ф 0, получаем а — ае = 0. Значит, е является единицей кольца R. ?

Рассмотрим два основных примера евклидовых колец.

Пример 2.24. Кольцо Z целых чисел — евклидово. Норма — это модуль числа. Свойства 1, 4 очевидны. Возможность деления с остатком тоже проверяется без труда: для a, b € Z, b > 0, обозначим q = max{s | а ^ sb}. Заметим, что qb 4- Ъ > а. Поэтому если а ф qb, то дчя г = а — qb выполнено г < Ь. Для b < 0 полагаем q = min{5 | а ^ sb], свойства остатка проверяются аналогично.

Пример 2.25. Пусть F — некоторое поле. Оказывается, что кольцо многочленов F[x] над полем F — евклидово. Норма — это степень многочлена.

По следствию 2.11 в кольце F[x] нет делителей 0, так как их нет в поле F (см. утверждение 2.21).

По утверждению 2.10 степень произведения двух ненулевых многочленов равна сумме степеней сомножителей, отсюда следует свойство 4 из определения евклидова кольца.

Делить многочлены с остатком можно «в столбик», как учат в школе делить обычные целые числа. Формально возможность деления с остатком можно проверить по индукции. Пусть мы рассматриваем деление с остатком на многочлен д (х) = до + 9ix + У**² + • • • + 9dX^d, 9d Ф 0. Для многочленов / степени меньше d имеем представление / = 0? д + /, deg / < deg#. Это база индукции. Теперь предположим, что мы умеем делить с остатком на д многочлены степени меньше п. Рассмотрим многочлен степени п:

Многочлен / = / — /п#^ ^{1 xU}~^d9 имеет степень, меньшую п, поэтому его можно разделить с остатком на д:

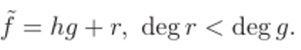
Но тогда.

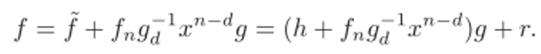
Значит, / также можно разделить на д с остатком.

Замечание 2.26. В определении деления с остатком мы не требовали единственности неполного частного и остатка. Это требование не нужно для доказательства основных свойств евклидовых колец. Отмстим, однако, что для кольца многочленов, как и для кольца целых чисел, неполное частное и остаток определены однозначно.

Действительно, пусть / = qg + r = q₂g + г₂. Тогда (Qi ~ (72)9 + (**2 — п) = 0. Из этой формулы сразу получаем, что Qi = q-2, так как deg г, < deg <7. Но тогда и г = г₂.

Далее мы рассматриваем только евклидовы кольца.

Теорема 2.27. Евклидовы кольца — это кольца главных идеалов.

Обратное, вообще говоря, неверно.

Доказательство. Пусть I С R — идеал. Предположим, что элемент а Е I имеет наименьшую норму среди всех ненулевых элементов идеала. Теперь возьмем любой другой элемент идеала b и разделим его на а с остатком: 6 = qa 4- г, N® < N (a). Но г = b — qa Е /, поэтому в силу минимальности нормы а получаем, что г = 0, т. е. b = qa. Таким образом, I = (а). ?

Пусть а, Ь — два элемента (евклидова) кольца R. Наибольшим общим делителем, а и b называют такой элемент d, что а = qd, b = rd, и для любого общего делителя d! (а = q’d', b = r’d') выполнено d = d’d." для какого-то d" Е R. Наибольших общих делителей в смысле данного определения может быть много. Скажем, 5 и —5 являются наибольшими общими делителями чисел 10 и 15 в кольце Z.

Пусть di и с/₂ — два наибольших общих делителя. Тогда по определению d = d’d₂ = d’d" d, т. е. d’d" = 1. Мы видим, что наибольшие общие делители отличаются на множитель, для которого в кольце есть обратный. И наоборот, если d — наибольший общий делитель, а е — обратимый элемент (делитель единицы), то ed — также наибольший общий делитель. Действительно, если а = qd, b = rd, то а = (qe~^l)(ed), b = (ге^-1)(?</); если d = d’d", то ed = (ed')d" .

Итак, наибольшие общие делители отличаются множителями, которые являются делителями единицы.

Два элемента кольца называются ассоциированными, если они различаются делителями единицы: а ~ b равносильно а = eb,? — делитель единицы. Ассоциированность является отношением эквивалентности. Несложная проверка этого утверждения оставляется читателю в качестве упражнения.

Мы будем обозначать наибольший общий делитель через (а, Ь) и понимать под этим традиционным обозначением любой из наибольших общих делителей.

Теорема 2.28. Наибольший общий делитель двух элел1ентов евклидова кольца можно представить как линейную комбинацию элементов а, Ь с коэффициентами из кольца: (а, Ь) = = га + qb, r, q € R.

Доказательство. Рассмотрим множество /, состоящее из всех элементов кольца вида га -t- qb, г, q е Л. Проверим, что это множество — идеал:

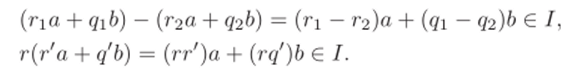
Поскольку кольцо евклидово, то этот идеал — главный, т. е. I = (d).

Докажем, что d — наибольший общий делитель а, Ь. Вопервых, поскольку а = еа + 06 € /, b = 0а + eb е /, получаем, а = 5(/, b = td. Во-вторых, поскольку del, его можно представить в виде d = га + qb. Значит, если а = q’d', b = г*d!, то.

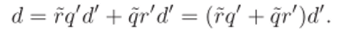
Как уже было показано, любой другой наибольший общий делитель d отличается от d на множитель е, который является делителем единицы. Поэтому d = (er)a + (eq)b. ?

Замечание 2.29. Обозначение (а, Ь) двусмысленно: так обозначается нс только наибольший общий делитель элементов а, 6, но и идеал, порожденный элементами а, b (наименьший идеал, содержащий эти элементы). В случае евклидовых колец эта двусмысленность не существенна, поскольку идеал (а, Ь) является главным идеалом, порожденным наибольшим общим делителем (а, Ь).

Элементы евклидова кольца R называются взаимно простыми, если их наибольший общий делитель равен единице.

Частным случаем теоремы 2.28 является основная теорема теории делимости: если числа п и т взаимно просты, то можно подобрать два таких целых х и у, что хп + ут = 1. Ясно также, что из теоремы 2.28 следует, что для любых двух целых п, т можно подобрать такие целые числа х, у, что хп + ут = (п, га). Используя эти утверждения, можно определить порядок элемента в циклической группе С_п и описать все порождающие элементы С_п.

Утверждение 2.30. Пусть т — целое число. Тогда порядок т в аддитивной группе Ъ_п вычетов по модулю п равен d = — n/(n, m).

Доказательство. Во-первых, dm = dm = п • (ш/(п, га)) = = 0. Во-вторых, если sfh = 0, s Ф 0, то sm = tn. Так как (п, гп) = хп + ут, то s (n, т) = sxn + sym делится на п. Но тогда s (n, т) ^ п и s ^ d. ?

Следствие 2.31. В аддитивной группе Z_r, порождающими элементами являются в точности те вычеты х, для которых (п, х) = 1.

Вернемся к общей теории. Пусть есть три элемента а, Ь, с целостного кольца с единицей и а = be. Рассмотрим идеалы (а), (6), т. е. все кратные а и все кратные Ь. Имеет место Утверждение 2.32. (а) С (6).

Доказательство. Возьмем какой-нибудь элемент из идеала (а). Он может быть представлен в виде ad. = b (cd) G (6). ?

Если элемент b ассоциирован с а, т. е. b = а • е, то, а = 6 • е~^х. Следовательно, (а) С (6), (b) С (а) и поэтому (а) = (6). Другими словами, если два элемента различаются делителем единицы, то они порождают одинаковые идеалы.

Элемент b называется собственным делителем ненулевого элемента а, если а = Ьс и 6, с необратимы.

Утверждение 2.33. Пусть b — собственный делитель а. Тогда, а не является делителем b, т. е. b ф ad.

(Значит, b? (а) и потому (а) С (6).).

Доказательство. От противного. Пусть а = Ьс. Предположим, что b = ad. Тогда а = a (cd) и а (1 — cd) = 0. Так как мы рассматриваем кольца без делителей нуля, то по крайней мере один из сомножителей в левой части равен 0. Поскольку а ф 0, то 1 = cd. Элемент d — обратный к с, приходим к противоречию. ?

Лемма 2.34. Если, а ф 0 разлагается в произведение собственных делителей Ьс, то N (b) < N (a).

Доказательство. Разделим b на а с остатком: b = qa -Ь г. Поскольку b — собственный делитель, то г Ф 0, N® < N (a). Но а = Ьс. Поэтому b = qcb + г, т. е. г = 6(1 — qc) ф 0. Следовательно, N (a) > N® ^ А^г(6) (норма произведения не меньше нормы ненулевого сомножителя). ?

Попутно, для завершения картины, выведем из этой леммы еще одну несложную теорему. Элемент кольца называется простым, если у него нет собственных делителей, а он сам не является делителем единицы.

Теорема 2.35. Каждый элемент евклидова кольца разлагается в произведение простых элементов и делителя единицы.

Доказательство. Индукция по величине нормы. В качестве базы индукции рассмотрим утверждение теоремы для элементов с минимальной нормой. Очевидно, что они простые: в противном случае они имели бы собственные делители, и эти делители имели бы меньшую норму.

Предположим, что утверждение теоремы верно для всех значений нормы, меньших либо равных некоторому числу т. Возьмем следующее значение нормы ra + .s, т. е. наименьшее из значений нормы, ббльпшх гп (существенное отличие от стандартной индукции здесь в том, что никто не утверждает, что значения норм идут подряд). Пусть N (a) = m + s. Если а — простой элемент, то утверждение выполняется. Если а — не простой, то он разлагается в произведение собственных делителей, норма которых меньше нормы а: а = be, N (b) < iV (a), N© < N (a). Для Ь, с утверждение справедпиво в силу предположения индукции, значит оно справедливо и для а. ?

Мы уже доказали (утверждение 2.33) что непростой элемент не можег породить максимальный идеал (равносильная форма: всякий главный максимальный идеал порождается простым элементом). Верно и обратное:

Теорема 2.36. Простой элемент р порождает максимальный идеал (р).

Доказательство. По теореме 2.22 идеал является максимальным тогда и только тогда, когда кольцо классов вычетов по этому идеалу является полем, т. е. разрешимо уравнение ах = 6, а Ф 0. Докажем, что в кольце R/(p) такое уравнение обязательно разрешимо.

Рассмотрим наибольший общий делитель (а, р). Так как р — простой, его делители — только единицы и ассоциированные с р элементы. Но а на р не делится (а ф б, значит, а (р)). Поэтому (а, р) — делитель единицы. По теореме 2.28 единицу можно представить в виде линейной комбинации а и р:

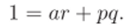
Докажем, что rb — решение уравнения ах = Ь. Так как b = = 16= (ar + pq)b = a (rb) 4- p (qb), то.

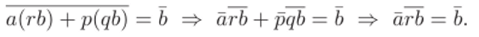
Итак, мы доказали, что любое линейное уравнение разрешимо, значит, кольцо классов вычетов R/{p) иоле, а потому идеал (р) — максимален. ?

В евклидовых кольцах существует простой способ нахождения наибольшего общего делителя и решения уравнения ха+ yb = (а, 6), который называется расширенным алгоритмом Евклида.

Утверждение 2.37. Для любых элементов a, b, q евклидова кольца выполнено (а, 6) = (а — qb, 6).

Доказательство. Пусть d — общий делитель а и 6, т. е. а — о! d, b — b’d. Тогда а — qb = a’d — qb’d — (а' — qb')d, гак что d является общим делителем а — qb и Ь. И наоборот, если a—qb = cd, b = b’d, то а = qb—cd = (qb'—c)d. Значит, множество общих делителей для пар а, b и а — qb, b одинаково. ?

Утверждение 2.38. Решениями однородного линейного уравнения с двумя переменными ах + by = 0 с коэффициентами из евклидова кольца R (а и b не равны одновременно нулю) являются

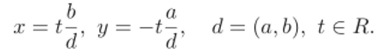
Доказательство. Разделив обе части уравнения на наибольший общий делитель (а, 6), получим равносильное уравнение, коэффициенты которого взаимно просты. Поэтому достаточно решить уравнение ах 4- by = 0 со взаимно простыми коэффициентами.

Если (a, b) = 1, то по теореме 2.28 для некоторых u, v Е R выполнено аи 4- bv = 1. Умножим равенство ах 4- by = 0 на и:

и (ах + by) = иах 4- uby = (1 — bv)x 4- иЪу = х 4- b (by — их) = 0.

Таким образом, х = tb при некотором t Е R. Но тогда by = = —ах = —tab и у = —ta. С другой стороны, любая пара (tb, —ta) является решением уравнения ах 4-by = 0. ?

Расширенный алгоритм Евклида работает следующим образом. Вначале вычисляется последовательность остатков (собственно алгоритм Евклида):

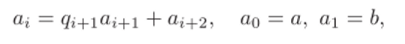
пока а*+2 0. Последние числа в этой последовательности.

a_t = qt+iat+i, a_t+1, причем a_t+1 = (a_0?ai) = (a, 6).

Почему алгоритм Евклида работает конечное число шагов и дает правильный ответ? Нормы элементов а, уменьшаются при г > 1, поскольку каждый следующий элемент является остатком от деления на предыдущий. Значит, после конечного числа шагов остаток станет нулю. Корректность ответа следует из утверждения 2.37:

Вторая часть алгоритма (расширенный алгоритм Евклида) строит последовательность пар Х{, у*, начиная с x_t = -1, yt. = Qt+i 4−1 по следующим рекуррентным формулам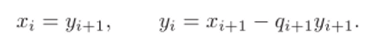

По индукции проверяется, что.

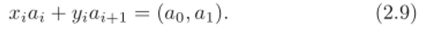
Это верно при i = t, так как.

Если (2.9) верно при i + 1, то оно верно и при г:

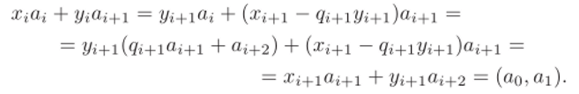
Пара (хо, уо), полученная в результате работы второй части алгоритма, будет решением уравнения ах + by = (а, Ь). Остальные решения отличаются от этого на решение однородного уравнения, так как если ахо + Ьуо = (о, 6) и ах + by = = (а, 6), то (ах + by) — (ахо + Ьу₀) = а (х — ж₀) + Ку ~ Уо) = 0. Поэтому общее решение линейного неоднородного уравнения имеет вид.