Корни многочленов над конечным полем

Теперь будем решать уравнения в конечном поле. Рассмотрим иоле GF (pⁿ), а в нём — какой-нибудь элемент 0, и будем интересоваться многочленами, для которых этот элемент является корнем.

Определение 3.29. Многочлен т (х) называется минимальной функцией для 0, если т (х) — нормированный¹) многочлен минимальной степени, для которого 0 является корнем. Другими словами, должны выполняться три свойства:

• а) т ()3) = 0;
• б) /(/?) Ф 0 при f (x) ф 0, deg f (x) < degm (a:);
• в) коэффициент при старшей степени в т (х) равен 1.

Пример 3.30. Пусть поле представлено как кольцо классов вычетов по модулю неприводимого многочлена а (х) = ао + + ах + • • • + а_пх^п. Для класса вычетов {х} полином а~^га (х) является минимальной функцией. Действительно, {х} является его корнем:

т. е. {х} — корень а (х), но тогда {х} является корнем и а"¹а (х). Докажем минимальность. Предположим, что существует многочлен Ьо + Ьх 4- • • • -I- 6_n_ix^n₁, для которого.

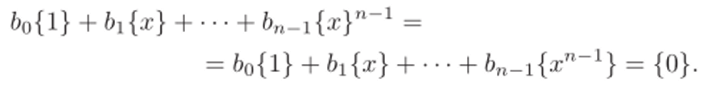
Это равенство задает линейную зависимость между {1}, {х}, {х²}, … {х^п-1}, которые образуют базис поля как векторного пространства над GF (p). Поэтому все 6* = 0.

Приведем несколько простых свойств минимальных функций.

Утверждение 3.31. т (х) — неприводимый, многочлен.

Доказательство. Предположим, что т (х) = mi (x)m2(x), причем degmj (x) > 0, поскольку многочлены нулевой степени — константы — образуют группу обратимых элементов в кольце многочленов над нолем. Но гп (в) = 0, поэтому хотя бы один из множителей или гаД/З) также должен равняться нулю (в поле делителей нуля нет). Значит, один из сомножителей имеет корень /9, а его степень меньше степени т (х). Это противоречит минимальности т (х). ?

Утверждение 3.32. Пусть т (х) — минимальная функция для /3, и Р также является корнем многочлена /(х). Тогда /(х) делится натп (х).

Доказательство. Разделим /(х) на ш (х) с остатком: /(х) = = и (х)тп (х) + v (x), degt; < degm. Подставляя в это равенство /9, получаем 0 = /(/9) = = v (/3). Т. с. /9 является корнем ц (х), что противоречит минимальности га (х). ?

Следствие 3.33. Для каждого р есть ровно одна минимальная функция.

Действительно, пусть минимальных функций две. Они взаимно делят друг друга, а значит, различаются на обратимый множитель (константу). Поскольку минимальная функция нормирована, эта константа равна 1, т. е. функции совпадают.

Утверждение 3.34. Для каждого /3? GF (pⁿ) существует минимальная функция и ее степень не превосходит п.

Доказательство. Рассмотрим следующие элементы поля: 1, /3, /З², …, /З^п, их п + 1 штука, а размерность GF (pⁿ) как векторного пространства над GF (p) равна п. Значит, эти элементы линейно зависимы, т. е. существуют такие коэффициенты со,…, с", что.

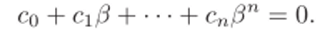
Следовательно, /3 — корень многочлена Со—CX-——--с_пх^п. Значит, минимальной функцией для /3 какой-нибудь будет нормированный неприводимый делитель этого многочлена. ?

Теорема 3.35. Любой ненулевой элемент поля GF (pⁿ) является корнем многочлена х^р «¹ — 1.

Доказательство. Ненулевые элементы поля образуют группу по умножению, порядок этой группы равен р^п — 1. Порядок любого элемента (т. е. порядок циклической подгруппы, порожденной этим элементом) по теореме Лагранжа делит порядок группы. Возьмем произвольный элемент а, обозначим его порядок через к. Тогда р^п — 1 = kq, or = 1, откуда получаем.

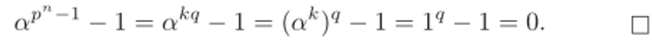
Следствие 3.36. Все элементы поля GF (pⁿ), не исключая нуля, являются корнями многочлена х^р — х.

Доказательство. Вынесем х за скобку:

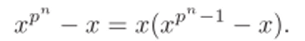
У правого множителя корнями будут все ненулевые элементы, а у левого — 0. ?

Теорема 3.37. Многочлен х^п — 1 делится на х^т — 1 тогда, и только тогда, когда п делится на т.

Доказательство. Пусть п = тк. Сделаем замену переменных: х^т = у. Тогда х^п — 1 = у^к — 1, а х^т — 1 = у — 1. Делимость очевидна, поскольку 1 является корнем у^к — 1.

Предположим, что п не делится на га, т. е. п = кгп 4- г, О < г < га. Запишем тождество.

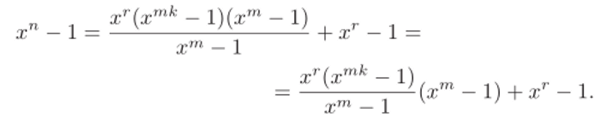
Последнее выражение задает результат деления х^п — 1 на х^т—1 с остатком, поскольку х^тк—1 делится на х^т — 1 но доказанному выше. Остаток х^г — 1 ф 0 в силу сделанных предположений. Поэтому в этом случае х^п — 1 не делится на х^т — 1. ?

Эта теорема дает нам возможность раскладывать некоторые многочлены х^п — 1. Например, пусть мы работаем в характеристике 2 (где 4−1 = —1), разложим ж¹⁵ 4−1:

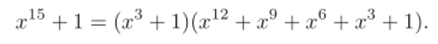
Продолжить это разложение помогает следующая теорема.

Теорема 3.38. Все неприводимые многочлены п-й степени над GF (p) являются делителями х^р — х.

Доказательство. Если п = 1, то нужно проверить, что х — а, где а € GF (p), является делителем х^р — х. Это очевидно при а = 0. В остальных случаях нужно проверить, что а — корень многочлена х^р~¹ — 1, что уже сделано выше в теореме 3.35.

При п > 1 строим по неприводимому многочлену f (x) степени п поле GF (pⁿ). Тогда многочлен f (x) имеет в GF (pⁿ) корень {х} и, более того, нормированный f (x) является минимальной функцией для {.т}, поскольку степени {;г} образуют базис в GF (pⁿ). С другой стороны, {т} является корнем уравнения х^{р _1} — 1. По утверждению 3.32 о минимальной функции многочлен х^{р _1} — 1 делится на /(#). ?

Используя эту теорему, мы можем завершить разложение х¹⁵ — 1: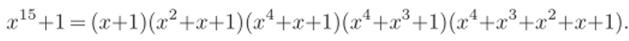

Теорема 3.39. Любой неприводимый делитель многочлена _хр ^-1 — 1 имеет степень, не превосходящую п.

Доказательство. Пусть <�р — неприводимый многочлен степени /г, который является делителем х^р — х. Кратные р образуют максимальный идеал в кольце GF (p)[x], поэтому кольцо вычетов по этому идеалу является полем. Поле можно рассматривать как векторное пространство над GF (p), базисом этого пространства является набор степеней {1}, {#}, {аг¹}. Далее будем обозначать {х} = а. Поскольку х^р' — х делится на <�р, то в кольце вычетов по модулю идеала (р) получаем а^р — а = 0.

Любой элемент построенного поля есть линейная комбинация базисных элементов:

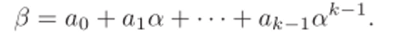
Возведем и левую, и правую части этого равенства в степень р^п, получим.

Отсюда получаем соотношение р^р" — 0 = 0, значит, — корень уравнения х^р — х = 0. Но у этого уравнения не более чем р^п различных корней, а в построенном нами поле — р^к элементов. Каждый элемент поля является корнем, следовательно р^п ^ ^ р^к, т. е. п ^ к. ?

Утверждение 3.40. Пусть некоторый элемент , 3 конечного поля имеет порядок L, а минимальная функция т{х) этого элемента имеет степень к. Тогда р^к — 1 делится на ?, а если г < к, то р^г — 1 не делится па ?.

Доказательство. По сути это прямое следствие только что доказанной теоремы.

По неприводимому многочлену А;-й степени т (х) можно построить поле из р^к элементов. Ненулевые элементы этого поля, в том числе и /9, являются корнями уравнения х^р ~¹ — 1 = 0,.

т. e. (3^pk~^l — 1=0, j3^pK~^l = 1. Это доказывает первую часть утверждения.

Вторая часть доказывается от противного. Предположим, что р^г — 1 делится на ? и г < к. Тогда {3 — корень уравнения х^р — 1 = 0. Так как т (х) — минимальная функция для /3, то х^р — 1 делится на т (х) (утверждение 3.32). Получается, что мы нашли неприводимый делитель многочлена х^р — 1 степени к. По к > г, что противоречит доказанной выше теореме 3.39. ?

Следующая теорема нужна нам для того, чтобы раскладывать многочлены на множители.

Теорема 3.41. Пусть & € GF (pⁿ) — корень неприводимого многочлена ip (x) степени п с коэффициентами из GF (p). Тогда f3, /З^р, …, /З^р все различны и исчерпывают список корней этого .многочлена.

Т. е. чтобы получить все корни неприводимого многочлена, достаточно найти один из них и возводить его последовательно в степень р.

Доказательство. Вначале докажем, что если (3 — корень у?(х), то (З^р — тоже корень.

Как было показано выше, а^р = а для всех а € GF (p). Поэтому для любого многочлена f (x) с коэффициентами из GF (p) выполняется равенство.

Действительно, возведение в степень р сохраняет операции сложения и умножения (см. выше раздел 3.2). Поэтому.

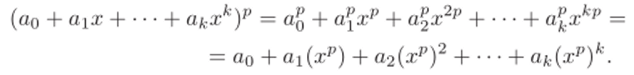
Если v?(/3) = 0, то и ?>(/3)^р = 0. Из (3.8) получаем, что и.

= о.

Итак, мы доказали, что /9, (З^р, …, /З^р — корни многочлена ц>(х). Осталось доказать, что они все различны, тогда из леммы 3.7 будет следовать, что мы нашли все корни многочлена <�р (х).

? к

Предположим, что (З^р = fi^p, причем без ограничения общности Р ^ к. Мы знаем, что j3^p = ft. С другой стороны, поскольку.

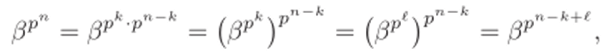
то в — корень уравнения х^{рп к+е}~¹ — 1 = 0. Из теоремы 3.38 получаем п — к + i ^ п, так что Р ^ к. Другими словами, Р = к и все выписанные выше корни различны. ?

Пример 3.42. Рассмотрим GF (2) и неприводимый над этим нолем многочлен четвертой степени х⁴+х³+1. Найдем его корни. Для этого строим расширение GF (2⁴) как кольцо вычетов по модулю идеала, образованного всеми кратными этого многочлена. Один корень получаем немедленно: {.т}. Теперь по теореме 3.41 можно выписать остальные: {х²}, {х⁴} = {х³ + 1}, {х⁸} = {х⁶ + 1} = {х³ + х² 4- х}, так как {х⁵} = {х⁴ Их} = = {х³ + хI-1}, {х⁶} = {х⁴ + х² + х} = {х³ -Ь 1 + х² + х}.

Таким образом, если мы решаем уравнение /(х) = 0, где / — неприводимый многочлен, то нужно построить по идеалу (/) поле. Первый корень есть сразу, это {х}. Остальные получаются применением теоремы 3.41. В общем случае для решения уравнения нужно уметь раскладывать многочлен на неприводимые множители.