Риск и неопределенность как экономические категории

Многие ситуации в деятельности потребителя и фирмы предполагают наличие нескольких исходов, нескольких вариантов развития событий. Например, компания может ожидать, что в следующем месяце при благоприятном ходе дел ее доход составит 20 тыс. руб., при нейтральном исходе — 10 тыс. руб. и при неблагоприятной ситуации будет равен всего 1 тыс. руб. Но какой именно сценарий будет реализован? Каким окажется его доход в действительности? Заранее, сегодня, в момент выбора, сказать невозможно. Это и есть неопределенная ситуация.

Экономисты различают понятия неопределенности и риска.

Неопределенность — ситуация, в которой возможны многие исходы (как благоприятные, так и неблагоприятные или нейтральные) и их вероятности неизвестны.

Риск:

• • ситуация, когда известны вероятности исходов;
• • вероятность неудачи проекта.

Варианты развития событий рассматриваются в экономике как исходы, в виде набора товаров, в форме денежных выплат (выручки, прибыли, дохода), доли рынка или еще какого-либо значимого параметра деятельности фирмы или индивида. Для удобства и с целью упрощения анализа обычно анализируются стоимостные результаты (доход, прибыль, цены, издержки). Для описания альтернатив, связанных с принятием решений, используется концепция лотереи. Лотерея — это набор исходов с указанием их вероятностей. Выбор индивида осуществляется между различными лотереями. Сам выбор может трактоваться как игра — поведение компании и индивида в условиях неопределенности и риска. Под игрой понимается процесс принятия решений, в котором участвует как минимум две (и более) стороны, которые соперничают за реализацию собственных интересов. Каждая из сторон имеет свою цель и использует некоторую стратегию, которая может вести к выигрышу или проигрышу — в зависимости от поведения других игроков. Экономика и теория игр помогают участникам (игрокам) выбрать наилучшие стратегии, с учетом ожиданий и действий других игроков, собственных и чужих ресурсов, на основе теоретически обоснованных прогнозов.

Вероятность исхода — это величина, которая показывает, насколько правдоподобно наступление определенного исхода. Можно выделить субъективную и объективную вероятности. Субъективная вероятность формируется на основе личного опыта индивида и мнения экспертов, объективная вероятность показывает частоту события в прошлом. Вероятность измеряется либо в долях, либо в процентах. Мы можем сказать: «Вероятность получения дополнительной прибыли в этом году составит 60%, или 0,6». Так как хоть какой-то вариант развития событий будет реализован, то сумма всех вероятностей для какой-либо фирмы или какого-либо индивида составляет 100%, или равна единице.

Поскольку решения на фирме принимаются людьми, целесообразно начать анализ ситуации неопределенности и риска с выбора индивида.

Итак, сосредоточимся на понимании того, каким образом индивид принимает решения в этих условиях.

Исследование выбора индивида в условиях неопределенности и риска требует принятия следующих предпосылок:

• 1) индивиду важны итоговые вероятности исхода, а не то, как они получены. Индивид не подвержен иллюзии риска. Источник неопределенности для индивида не важен до тех пор, пока это не отражается на итоговой вероятности исхода;
• 2) вероятности исходов известны индивиду;
• 3) множество вероятностей исходов замкнуто и непусто (индивид будет реализовывать хоть бы одну стратегию, не отказывается от выбора);
• 4) индивид не может оказать влияние на вероятности исходов;
• 5) отношения предпочтений непрерывны, так что небольшие изменения вероятности не изменяют порядка предпочтения между двумя и более лотереями;
• 6) исходы взаимоисключают друг друга и не зависят друг от друга. Поэтому сумма вероятностей всех исходов равна единице: Хр, = 1, где р (probability) — вероятность /-го исхода. Какой-нибудь исход обязательно осуществится;
• 7) отношения предпочтений лотерей транзитивны (люди в целом склонны поступать логично);
• 8) предпочтения возрастают с увеличением вероятности. Индивид предпочитает лотерею с большей вероятностью высокого дохода. Две лотереи с одинаковыми вероятностями высокого дохода рассматриваются индивидом как эквивалентные.

В дальнейшем мы будем рассматривать вероятности как заданные, поэтому необходимо понять, каким образом в принципе можно получить эти значения. Здесь представлены наиболее распространенные в экономическом анализе и в практике бизнеса формулы. За более детальной информацией можно обратиться к специальной литературе по теории вероятности и математической статистике.

Для продвинутых читателей Вопросы теории Есть несколько способов нахождения теоретической вероятности анализируемых исходов. Поскольку эти методы базируются на теории, а не на частоте события, полученной в ходе прошлого опыта или эксперимента, найденная вероятность называется теоретической.

1. При биноминальном распределении X:

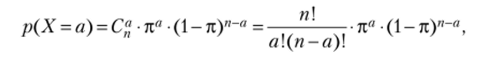
где р (Х = а) — вероятность того, что X принимает значение а; а — успешные попытки; п — вероятность успешной попытки в единичном испытании (относительная частота успешного события).

2. При стандартном нормальном распределении:

X- — х

1) находим нормированное значение величины: z = —-, где — наблюдаемое зна;

G.

чение величины; х— среднее значение выборки; а — стандартное отклонение выборки;

• 2) находим вероятность по статистической таблице.
• 3. При распределении Пуассона:

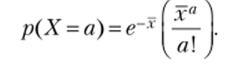
Если некоторое событие происходит случайно и независимо в каждой из попыток и среднее число наступлений события с ростом числа попыток не изменяется, то количество наступлений события в фиксированном количестве попыток будет подчиняться распределению Пуассона.

Распределение Пуассона — это распределение дискретной величины, которое зависит только от ожидаемого среднего количества наступлений события. Например:

• • количество заказов, которые фирма получит завтра;
• • количество людей, которые обратятся завтра в отдел кадров компании;
• • количество дефектов в произведенной продукции;
• • количество людей, которые завтра обратятся за гарантийным ремонтом изделия;
• • биноминально распределенная величина X при больших п и малых п.
• 4. При экспоненциальном распределении:

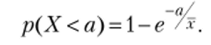
Экспоненциальное распределение имеет сильную асимметрию (рис. 5.1).

Рис. 5.1. Экспоненциальное распределение Этот вид распределения часто используется для представления времени ожидания между событиями, если сами события происходят случайно, независимо и с постоянной частотой. Например:

• • промежутки времени между появлением посетителей на фирме;
• • длительность типичного телефонного разговора;
• • время до выхода из строя компьютера;
• • затраты времени на обслуживание одного покупателя.

Дополнительно для понимания процесса вычисления и механизма действия теоретической вероятности можно рекомендовать следующий учебник: Сигел Э. Ф. Практическая бизнес-статистика: пер. с англ. СПб.: Вильямс, 2016.

Кроме вероятности исхода для характеристики риска и неопределенности могут использоваться показатели ожидаемой величины и разброса ожидаемой величины.

Математическое ожидание находится по формуле.

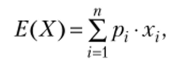
где Е (Х) (применяется также обозначение X^е) показывает ожидание величины X (или ожидаемое значение величины X); х_{ — возможное (допустимое) значение величины при i-м исходе; р_{ — вероятность /-го исхода; п — общее число исходов.

Математическое ожидание (или просто ожидание) характеризует средневзвешенное значение исходов. В качестве весов берутся вероятности исходов. Математическое ожидание показывает основную тенденцию изменения неопределенной величины.

В экономике математическое ожидание обычно рассматривается в его конкретной форме — ожидаемой полезности, ожидаемого дохода, ожидаемой прибыли.

Пусть, например, индивиду известны следующие варианты величины его будущего дохода и их вероятности (табл. 5.1). Варианты будущего дохода могут быть спрогнозированы на основе оценки будущего спроса (если индивид является предпринимателем или владельцем фирмы), будущих заработков (если индивид — наемный работник), предполагаемых грантов, состояния дел в отрасли или общей экономической конъюнктуры. Вероятности оцениваются либо экспертами, либо самим индивидом, исходя из своего предыдущего опыта.

Таблица 5.1

Условные значения для индивида.

Математическое ожидание дохода, или ожидаемый доход, для индивида составит:

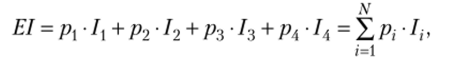
т.е. EI = 0,5- 50 + 0,25 • 100 + 0,2 • 200 + 0,05 800 = 130 (тыс. руб.).

Таким образом, индивид может ожидать, что в будущем (на следующий год или на следующий период планирования) в среднем его доход составит 130 тыс. руб.

Однако для фирмы и для индивида важное значение имеет не только сам по себе ожидаемый доход, но и разброс возможных его возможных значений. Вариабельность исходов выражается в двух показателях. Это:

• дисперсия: D (X) = o² =? Pi •(*, -Е (Х))²;

i=i

• среднеквадратическое отклонение о = .

Дисперсия случайной величины — мера разброса данной случайной величины, ее отклонения от математического ожидания. Обозначается как D (X) в русской литературе и как Var (X) (англ, variance) в зарубежной. В статистике часто употребляется обозначение о²_х или а².

Квадратный корень из дисперсии, равный а, называется среднеквадратическим отклонением, стандартным отклонением или стандартным разбросом. Стандартное отклонение измеряется в тех же единицах, что и сама случайная величина, а дисперсия измеряется в квадратах этой единицы измерения.

Случайная величина — это величина, которая принимает в результате опыта одно из множества значений, причем появление того или иного значения этой величины до ее измерения нельзя точно предсказать. Случайные величины используются для математического представления таких сторон объектов, систем и событий, количественную характеристику которых до проведения опыта по их измерению однозначно определить принципиально невозможно. Все ожидаемые показатели (будущие экономические индикаторы) в ситуации неопределенности являются случайными величинами.

Показатели дисперсии и среднего отклонения характеризуют степень изменчивости каждого конкретного исхода по сравнению со средней ожидаемой величиной. Чем больше дисперсия или среднеквадратическое отклонение, тем выше волатильность (вариабельность) исследуемой величины и тем выше риск ситуации.

Найдем дисперсию и среднее отклонение для ожидаемой доходности рассмотренного выше примера.

Дисперсия равна:

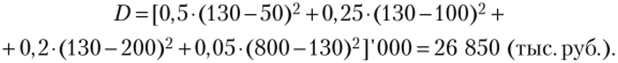
Среднее отклонение составит: о = 4Ъ = >/26 850 = 164 (тыс. руб.).

Это означает, что ожидаемый доход в 130 тыс. руб. может в среднем принимать значения от (130 + 164 = 294) тыс. руб. до (164 — 130 = 34) тыс. руб. Как мы видим, данная ситуация характеризуется большим разбором значений дохода, что означает ее высокую рискованность для индивида.

Достаточно ли знать ожидаемую доходность лотереи, чтобы определить выбор индивида? Оказывается, нет. Иллюстрацией этому служит так называемый парадокс Бернулли.

Предположим, индивиду предлагается поучаствовать в такой игре. Бросается монета. Если выпадает «орел», то игрок получает 2 руб. Если выпадает «решка», монету продолжают бросать далее. Если «орел» выпал на N-й попытке, то игрок получает 2^руб.

Найдем ожидаемую ценность (доходность) данной лотереи. Так как исходы независимы (предполагается честная игра со стандартными моне;

тами), то вероятность выпадения «орла» на попытке N составит: р = ——. 1о есть если «орел» выпадает при первой попытке броска монеты, индивид получает 2 руб. с вероятностью р_х = —; если при второй попытке — доход составит 4 руб. с вероятностью р₂ = —; если при третьей попытке — инди;

" 4.

вид получит 8 руб. с вероятностью = — и т. д. Ожидаемая доходность.

оо оо ^ ^

игры будет равна El = X (А • */) = X ²' «^7 г ⁺°°'.

|=1 i=i V ^z)

Однако, как заметил Даниил Бернулли, никто обычно долго в эту игру не играет и не готов много платить за участие в ней. Почему?

Размышления на эту тему позволили Бернулли выдвинуть концепцию ожидаемой полезности неопределенных исходов. Люди оценивают лотереи не по ожидаемой доходности, а на основе ожидаемой полезности возможных доходов.

Функция ожидаемой полезности показывает математическое ожидание полезности неопределенных исходов:

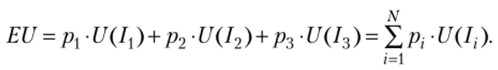
Существование функции ожидаемой полезности выводится на основе аксиом поведения индивида в условиях неопределенности и риска. Если эти предпосылки выполняются, то функция ожидаемой полезности существует, единственна, непрерывна, является возрастающей по доходу и линейна по вероятностям. Эта функция называется функцией полезности фон Неймана — Моргенштерна.

Пусть, например, полезность денежного дохода для индивида имеет вид: U (I) = V7. Тогда ожидаемая полезность игры Бернулли составит.

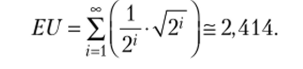
И цена игры — сумма денег, которую готов отдать индивид за участие в игре, будет равна I = EU² = (2,414)² = 5,76 (руб.). Парадокс Бернулли решен!

Важной характеристикой ситуации неопределенности и риска и выбора индивида является предпосылка о наличии безрискового денежного эквивалента лотереи.

Безрисковый эквивалент — это денежная сумма, которую индивид может получить, не участвуя в лотерее, и которая эквивалентна ожидаемой доходности лотереи. Для случая двух исходов безрисковый эквивалент равен.

где /₀ — величина безрискового эквивалента; 1_Х — доход при благоприятном исходе; 1₂ — доход при неблагоприятном исходе; р — вероятность благоприятного исхода; (1 — р) — вероятность неблагоприятного исхода.

Например, для рискового проекта с вероятностью 0,25 получения дохода в 100 тыс. руб. и вероятностью 0,75 получения дохода в 10 тыс. руб. безрисковый денежный эквивалент составит:

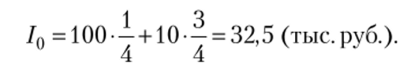
Это означает, что с точки зрения доходности индивиду все равно (безразлично, эквивалентно), получить 32,5 тыс. руб. безо всякого риска или участвовать в рисковом проекте с некоторыми вероятностями выигрыша и проигрыша.

Задача, иллюстрирующая концепцию:

Функция полезности индивида равна: U= 120 — 200: /, где U — совокупная полезность; / — доход потребителя. Потребителю предоставляется на выбор 4 тыс. руб. или лотерея, где он с вероятностью ¼ может выиграть 10 тыс. руб. или с вероятностью ¾ выиграть 2 тыс. руб. Что предпочтет потребитель: играть или получить безрисковый эквивалент игры?

Решение.

Полезность безрискового эквивалента равна U = 120 — 200: 4 = 70.

Ожидаемая полезность лотереи равна U₂ = (120 — 200 / 10) • ¼ +(120 — 200 / / 2) • ¾ = 40.

Так как U > U₂> потребитель предпочтет не играть, а получить безрисковый эквивалент.