Сопряжение в цепи

Особенно наглядно этот механизм повышения жесткости цепей проявляется в ароматических полиамидах /шра-структуры. В амидной группе вследствие квазисопряженного характера связей вращение сильно заторможено:

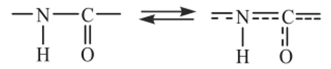
Поэтому полиамиды обладают высокой равновесной гибкостью только в том случае, когда амидные связи в цепи разделяются гибкими фрагментами, например мостиком из более чем четырех метиленовых групп. Большинство алифатических полиамидов является гибкоцепными полимерами — размер сегмента 2—3 нм.

При сближении амидных групп цепь становится более жесткой и в предельном случае, когда она построена только из амидных связей, как в полиалкилизоцианатах.

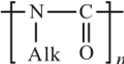
вращение оказывается невозможным. Линейные однотяжные цепи полиалкилилизоцианатов являются одними из наиболее жестких: значения А достигают у них 100 нм, что соответствует примерно 500 элементарных звеньев в одном сегменте Куна (см. табл. 1.8).

Высокая жесткость макромолекул полиалкилизоцианатов достигается за счет сопряжения между амидными группами цепи. Присоединение в поли-, м-толуиленизоциапате к атому азота вместо алкильного радикала ароматического заместителя нарушает сопряжение вследствие взаимодействия л-системы этого заместителя со свободной парой атома азота и исключения ее из сопряжения.

При этом сопряжение нарушается и цепь оказывается в 50 раз более гибкой:

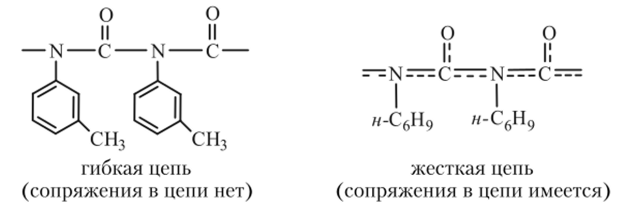
Аналогичная ситуация наблюдается и в полиамидах, в цепях которых амидные группы связаны с ароматическими радикалами в пара-положениях. К числу таких полимеров относятся:

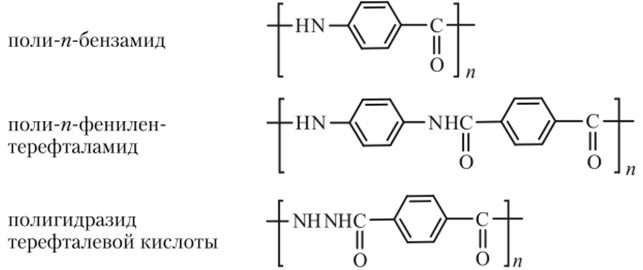
Приведенные в табл. 1.8 значения сегментов Куна этих полимеров свидетельствуют о высокой равновесной жесткости их макромолекул, обусловленной невозможностью вращения вокруг связей в амидных группах вследствие их квазисопряженного характера.

Механизмы изгибания жесткоцепных полимеров. При небольшой длине макромолекулы жесткоцепного полимера будут находиться только в конформации вытянутого стержня. В случае большой длины цепей такие стержни могут изгибаться по трем возможным механизмам.

• 1. Деформация валентных углов и длин связей («деформационный» механизм) может быть легко смоделирована на примере изгибания металлического провода или рельса большой длины.
• 2. Наличие дефектов в цепях, делающих их более гибкими вследствие появляющихся возможностей вращения, связано с нарушениями строения цепи при наличии примесей в исходных веществах или протекании побочных реакций в процессе образования полимера. Так, если в макромолекуле поли-я-фенилентерефталамида одно звено из ста окажется мета-изомерным, то гибкость цепи увеличится из-за нарушения сопряжения: вокруг одинарных связей С—N в этом звене станет возможным вращение и появится возможность к изгибанию.
• 3. Изгибание, обусловленное неравенством валентных углов некоторых связей основной цепи, можно проследить па примере цепи пара-ароматического полиамида:

Вокруг связи C-N вращение амидной группы невозможно, но оно может быть осуществлено вокруг одинарных связей С_арил—С и N—С_арил. Если валентные углы аир при атомах С и N равны, то вращение вокруг связей между ароматическими циклами и амидной группой приведет к конформации цепи типа «коленчатый вал» (рис. 1.13, а).

Однако, по литературным данным, углы, а и р различаются и для приведенных ароматических пара-полиамидов р — а = До = 6-Н2°. Следовательно, вращение, схематически показанное на рис. 1.13, б, вследствие неравенства углов аир приведет к отклонению от вытянутой конформации типа «коленчатого вала» к изогнутой.

При большой длине жесткая цепь, изгибаясь, может образовать свернутую конформацию. Гибкая цепь имеет конформацию гауссова клубка (рис. 1.14, а), а жесткая — изогнутого стержня (рис. 1.14, б). Последняя отличается от гауссова клубка значительно большей рыхлостью, т. е. в среднем большими внутримолекулярными расстояниями между отдельными участками цепи.

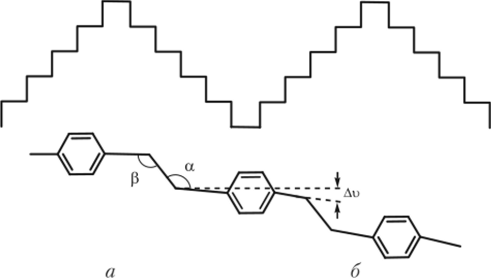
Рис. 1.13. Конформация цени нара-ароматического полиамида тина «коленчатый вал» в случае равных углов, а и Р при атомах углерода и азота (а) и конформация той же цени при, а > Р (б).

Рис. 1.14. Формы макромолекулярного клубка, образованного гибкой (а) и жесткой (б) макромолекулами одинаковой длины Применение классического конформационного анализа, основанного на модели свободносочлененных сегментов, для таких неплотных, рыхлых клубков невозможно. Поэтому для характеристики конформационных свойств макромолекул жесткоцепных полимеров чаще используют модель персистентной или червеобразной цепи. Персистентную цепь определяют как линию постоянной кривизны (рис. 1.15); мерой кривизны является «персистентная длина» а, определяемая из соотношения.

где L — контурная длина отрезка цепи (или всей цепи); ц/ — угол между направлениями отрезка кривой в его начале и конце; cos |/ — косинус угла, усредненный по всем конформациям цепи.

Приняв в уравнении (1.15) L = а, получим / = 67°. Следовательно, количественной мерой персистентной длины цепи может служить такая длина ее отрезка, что угол между касательными в начале и конце его составляет 67°. Как можно отметить из рассмотрения рис. 1.15, для жесткой цепи значение а существенно выше, чем для гибкой. Величина сегмента Куна А связана с персистентной длиной цепи а простым соотношением А = 2а.

Рис. 1.15. Модель персистентной цепи для жесткой (а) и менее жесткой макромолекул (б).

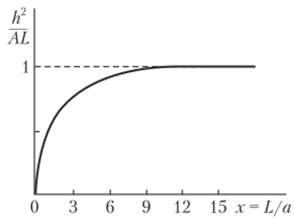
Рис. 1.16^ Зависимость отношения h²/(AL) от длины цепи х (х = L/a).

При очень большой контурной длине L (высокой молекулярной массе) жесткая цепь может образовать достаточно плотный клубок, по свойствам приближающийся к гауссовому. Для оценки степени отклонения свойств такого клубка от гауссова используют соотношение

где х = L/а.

Графически эта зависимость представлена на рис. 1.16, из которого следует, что любая по степени жесткости цепь может принять форму гауссова клубка, но для разных цепей этот переход осуществляется при разных значениях молекулярной массы (контурной дайны L). Если цепь гибкая (а мало), то она образует гауссовский клубок в растворе при сравнительно небольших молекулярных массах (порядка нескольких тысяч). В случае жестких цепей (А > 20 нм, а > 10 нм) форму гауссова клубка цепь может принять только при молекулярной массе выше нескольких десятков тысяч.

Еще одним критерием для оценки равновесной гибкости цепи является введенный П. Флори параметр гибкости /, обозначающий долю гибких связей в макромолекуле. Теоретически было показано, что если / > 0,63, то цепь можно считать гибкой, а при /< 0,63 — жесткой. Хотя это граничный параметр гибкости и является условным, однако он позволяет определить способность или неспособность полимеров к упорядочению в растворе или в расплаве (см. с. 521).