Оценочные функции. 
Химическая технология: научные основы процессов ректификации. 
Часть 2

Рассмотрим описание некоторой специальной оценочной функции и покажем, что ее использование максимизирует эффективность перебора схем разделения и в то же время гарантирует обнаружение пути минимальной стоимости, который ведет к нахождению оптимальной схемы разделения.

_# Определим оценочную функцию q так, чтобы значение q (х) для любой вершины д; представляло собой сумму оценки стоимости минимального пути от начальной вершины (дерева вариантов) В к вершине х и оценки стоимости минимального пути от вершины х к целевой вершине, соответствующей завершенной схеме.

Таким образом, q (х) представляет собой оценку стоимости минимального пути при условии, что этот путь проходит через вершину х. По этой оценке та вершина, которая имеет наименьшее значение q, считается лежащей на пути минимальной стоимости, и поэтому следующей должна быть раскрыта именно она.

Для иллюстрации некоторых из свойств этой оценочной функции введем ряд обозначений. Пусть функция R (B, x) определяет действительную стоимость минимального пути между двумя произвольными вершинами k (x_itXj), т. е. стоимость дуги, соединяющей эти вершины, и функция к не определена для вершин, между которыми нет пути. Если Т — множество целевых вершин, то стоимость минимального пути от вершины х, до цели обозначим.

Будем считать, что любой путь от вершины х к целевой вершине, для которого достигается h (xj, является оптимальным.

Как правило, требуется знание стоимости оптимального пути к (В, х) от начальной точки исходной вершины В до некоторой произвольной вершины х. Обозначения несколько упростятся, если ввести функцию R:

для всех х, достижимых из В.

Определим функцию q так, чтобы ее значение q (x) для любой вершины х составляло сумму действительной стоимости оптимального пути от вершины В до целевой вершины, т. е.:

Следовательно, значение q (x) есть стоимость оптимального пути при условии, что он проходит через вершину х.

Функция g есть оценка функции q. Она задается выражением:

где R* — оценка для /?; И* — оценка для И.

В качестве q*(x) выбирается стоимость пути от В до х на дереве вариантов, которая получается после суммирования стоимостей дуг, лежащих на пути к вершине х. (Предполагается, что это путь наименьшей стоимости от В до х, найденный по алгоритму к данному моменту).

Необходимым условием считается, что.

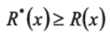
Из следующего примера видно, что эта оценка легко вычисляется в процессе поиска. Рассмотрим фрагмент дерева вариантов, показанный на рис. 9.5, на котором указаны стоимости дуг и их направления. Начиная поиск от вершины В, получаем следующие за ней вершины Х|, Х2- Оценки R (х) и R (хт) будут равны соответственно 2 и 5. Следующей, согласно алгоритму, раскрывается вершину Х2 и строятся вершины *з и *4. При этом R (хз) =2+2=4 и R (х^)=2+=Ъ. На следующем шаге будет раскрыта вершина х", так как к этой вершине найден менее дорогой путь. Для вершины *5 R (3с₅;=3+3=6.

Для проведения поиска требуется оценка h (х) для И (х). Здесь предлагается использовать эвристическую информацию, связанную с конкретной решаемой задачей. Функцию h принято называть эвристической функцией; более подробно мы рассмотрим ее ниже. Нетрудно заметить, что, если h’s 0, то алгоритм поиска становится алгоритмом слепого поиска, например методом постоянной стоимости или методом ветвей и границ. Следовательно, эти алгоритмы могут быть рассмотрены как частный случай более общего эвристического алгоритма.

Эвристический алгоритм поиска допустим, если для произвольного графа (дерева вариантов) он оканчивает свою работу построением оптимального пути к целиДнаходит оптимальный вариант схемы разделения). Если h — нижняя граница для h (h‘ < h), то эвристический алгоритм также допустим. Для доказательства сначала нужно убедиться в том, что до завершения работы эвристического алгоритма на выбранном оптимальном пути имеется некоторая вершина, значение q для которой меньше действительной стоимости q оптимального пути, проходящего через эту вершину. _t

Поскольку вершина, имеющая минимальное значение q , не может оказаться целевой вершиной (соответствовать завершенной схеме разделения) до тех пор, пока не будет найдена целевая вершина, значение q для которой равно q, эвристический алгоритм поиска допустим.

Таким образом, если эвристическая функция h является нижней границей для h, то, до того как эвристический алгоритм закончит свою работу (найдет целевую вершину), величина q не превышает действительной стоимости пути к оптимальному варианту т. е.

Это неравенство является необходимым и достаточным условием допустимости эвристического алгоритма при поиске оптимального пути. Основной трудностью при таком поиске является поиск самой^эвристической функции. Точность эвристической функции И зависит от объема тех «эвристических» знаний, которыми мы располагаем относительно конкретной решаемой задачи. При определении эффективности эвристического алгоритма поиска оптимального пути выбор функции h играет решающую роль. Использование.

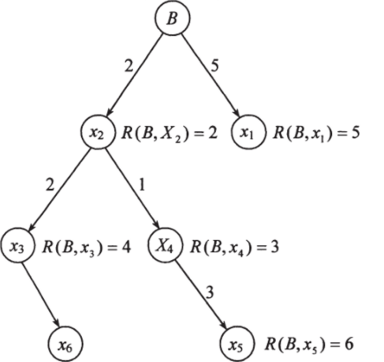
Рис. 9.5. Фрагмент дерева вариантов схемы разделения условия h‘ = О гарантирует допустимость, но ведет к слепому перебору и поэтому обычно оказывается неэффективным. Выбор в качестве А* наибольшей из возможных нижних границ для h приводит к тому, что раскрывается наименьшее число вершин, и это характеризует эффективность работы всего алгоритма.