Построение циркульных и лекальных кривых

Построение эллипса по двум его осям (рис. 2.35). На заданных осях эллипса — большой АВ и малой CD — построить как на диаметрах две концентрические окружности. Одну из них разделить на 8… 12 равных или неравных частей и через точки деления и центр О провести радиусы до их пересечения с большой окружностью. Через точки Г, 2, … деления большой окружности провести прямые, параллельные малой оси CD, а через точки 1', 2,… деления малой окружности — прямые, параллельные большой оси АВ. Точки пересечения соответствующих прямых принадлежат искомому эллипсу. Полученную совокупность точек, включая точки на большой и малой осях, последовательно соединить от руки плавной кривой, которую затем обвести по лекалу.

Построение овала. Овал — плоская, замкнутая, выпуклая, плавная кривая, состоящая из взаимно сопрягающихся дуг окружностей различных радиусов. Построение овала выполняется дугами окружностей из соответствующих центров О, 0₂, О_э и 0₄. Ниже приведены два способа построения овала, которыми с практической точностью можно заменить построение эллипса.

Построение овала по двум его осям. Первый способ (рис. 2.36). Для нахождения центров 0,0₂ необходимо: 1) отложить на малой оси отрезок ОЕ — О А (длину большой полуоси); 2) провести прямую АС и отложить на ней от точки С отрезок СК = СЕ; 3) восставить срединный перпендикуляр л к отрезку АК; 4) на пересечении с заданными осями овала отметить положение центров О, и 0₂. Два других центра О_э и 0₄ симметричны О, и 0₂ относительно точки О пересечения осей.

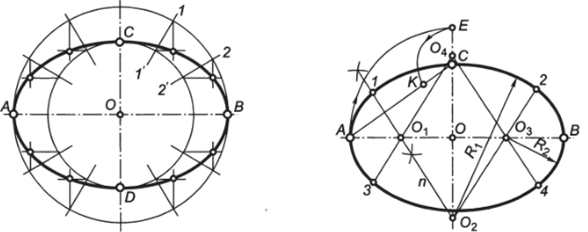
Рис. 2.35. Построение эллипса по двум его осям.

Рис. 2.36. Построение овала по двум осям овала; 5) из центров О, и О_э провести дуги окружностей радиусом Я₂;

Рис. 2.37. Построение овала при отношении осей >/3.

• 6) на продолжении лучей 0,0₂, 0₂0₃,
• 0₄0, и 0₄0₃, соединяющих найденные центры, отметить точки сопряжения 1,2,3,4 и соединить их дугами окружностей: Яj = 0₂2; Я₂ = О_э2.

Второй способ — при заданном соотношении осей АВ = л/ЗCD (рис. 2.37): 1) из центра О пересечения осей овала радиусом ОА провести дугу до пересечения с продолжением малой оси CD и отметить точки 0₂, 0₄; 2) аналогично радиусом ОС описать дугу до пересечения с большой осью АВ в точках О, и О_э; 3) провести лучи через полученные центры Oj… 0₄; 4) провести дуги сопряжения радиусами Я, = 0₂С, Я₂ = OjA до пересечения с лучами в точках 1,2, 3 и 4.

Построение овала делением большой оси на четыре равные части (рис. 2.38): 1) через центр О большой оси АВ перпендикулярно АВ провести малую ось; 2) из того же центра О радиусом OOj = = ОА/2 описать окружность и на ее пересечении с малой осью отметить центры 0₃ и 0₄; 3) из центров О, и 0₂ описать дуги окружностей радиусом Я, = О, А; 4) на продолжениях лучей, соединяющих центры малых и больших дут, отметить точки сопряжения 1, 2, 3 и 4 при их пересечении с дугами Я,; 5) из центров 0₃ и 0₄ провести дуги окружностей радиусом Я₂ = 0₃1, замыкающие овал.

Построение овала делением большой оси на три равные части (рис. 2.39): 1) разделить большую ось АВ овала на три равные части,.

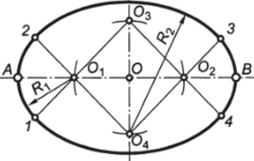
Рис. 2.38. Построение овала делением большой оси на четыре равные части.

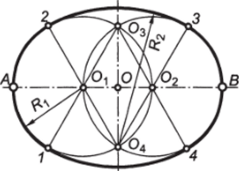
Рис. 2.39. Построение овала делением большой оси на три равные части отметив центры О, и 0₂; 2) описать из центров Oj и 0₂ окружности радиусом Я, = АВ/3 и отметить точки 0₃ и 0₄ их взаимного пересечения как центры сопрягаемых дуг овала; 3) на лучах, соединяющих центры спрягаемых дуг, при их пересечении с окружностями радиуса R_{ отметить точки сопряжения 1,2,3 и 4; описать дуги окружностей из центров О_э и 0₄, замыкающие овал.

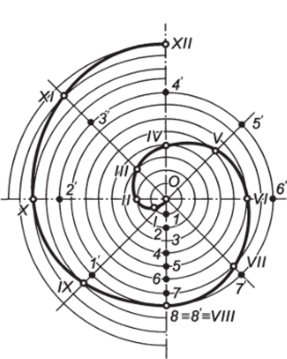
Рис. 2.40. Построение спирали Архимеда.

Построение спирали Архимеда (рис. 2.40). Спираль Архимеда — траектория точки, равномерно движущейся от центра окружности по радиусу, вращающемуся с постоянной угловой скоростью.

Для построения спирали Архимеда исходную окружность и ее радиус разделить на одинаковое число равных частей (на рис. 2.40 л = 8; 1, 2,…, 8 — точки деления радиуса; Г, 2 …, 8' — точки деления окружности). Через точки деления на окружности провести из центра О лучи, последовательно откладывая на каждом из них соответствующее число делений радиуса: на первом О Г — расстояние OI,

на втором 02' — расстояние 02 и т. д. Полученный ряд точек /, II…

VIII соединить плавной кривой и обвести ее по лекалу.

Построение эвольвенты (развертки) окружности по заданному диаметру (рис. 2.41). Исходную окружность с центром О разделить на произвольное число равных частей (л = 12). В точках деления 1, 2, … 12 провести касательные к окружности, направленные в одну сторону. Касательную, проведенную из последней точки деления, ограничить отрезком, равным длине окружности (2nR), и разделить этот отрезок на то же число равных частей. Последовательно отмечая на всех касательных точки, соответствующие определенному числу делений длины окружности: на первой — одному делению, на второй — двум и т. д., — соединить их плавной кривой линией.

Построение циклоиды (рис. 2.42). Циклоидой называют траекторию движения точки на окружности, перекатываемой без проскальзывания по прямой линии. Для построения циклоиды необходимо от начальной точки А окружности провести направляющую прямую, ограничив ее длину отрезком АА,₍ равным длине заданной.

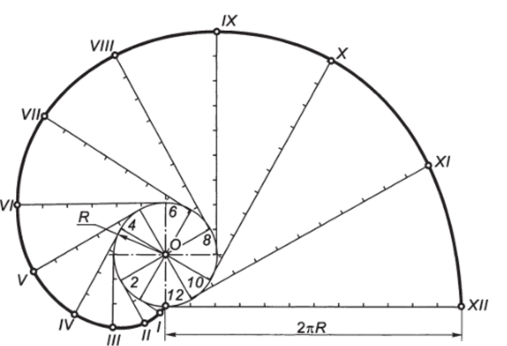
Рис. 2.41. Построение эвольвенты.

окружности (2nR). Разделить отрезком АА, окружность на одинаковое число равных частей (л = 12). Через точки деления окружности 1, 2 … провести ряд прямых параллельно направляющей прямой АА, а через точки деления прямой — перпендикуляры, которые при пересечении с осевой линией, продолженной из центра начальной окружности, обозначат ряд последовательно расположенных центров О, 0₂, … перекатываемой окружности. Описывая из этих центров дуги радиусом R, последовательно отметить точки их пересечения с соответствующими прямыми, параллельными АА, как точки, принадлежащие циклоиде.

Построение эпициклоиды и гипоциклоиды. Эти плоские кривые можно рассматривать как частные случаи циклоиды, где направляющей для перекатывания окружности служит дуга задан;

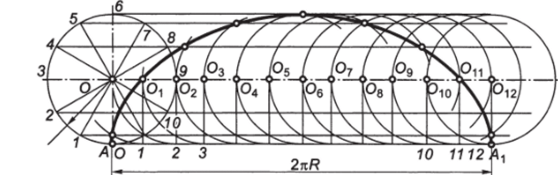
Рис. 2.42. Построение циклоиды.

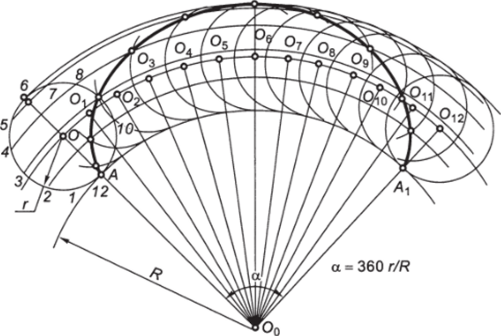
Рис. 2.43. Построение эпициклоиды.

ного радиуса. При перекатывании исходной окружности радиуса г по внешней стороне направляющей дуги радиуса R точка А описывает эпициклоиду (рис. 2.43), по внутренней стороне — гипоциклоиду (рис. 2.44). Длина дуги направляющей окружности определяется центральным углом, а = 360r/R. Построение точек эпициклоиды и гипоциклоиды аналогично построению циклоиды (см. рис. 2.42) при условии замены прямых, параллельных направ;

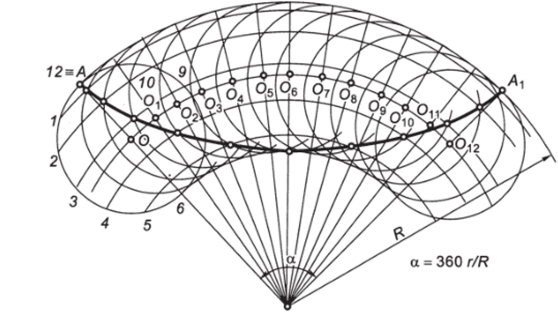
Рис. 2.44. Построение гипоциклоиды 58.

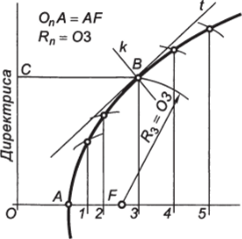
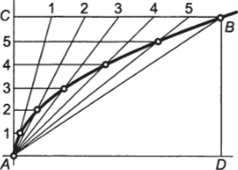
Рис. 2.45. Построение параболы Рис. 2.46. Построение параболы по директрисе и положению фокуса по ее вершине, оси и точке.

ляющей АА, дугами концентрических окружностей, а перпендикуляров к линии АА, — радиусами.

Эпициклоида, построенная при R = г, называется кардиоидой; гипоциклоида, полученная при R = 4 т, называется астройд о й. При R = 2 г гипоциклоида трансформируется в прямую, являющуюся диаметром направляющей окружности.

Построение параболы. Способ 1 — по заданным директрисе и положению фокуса F (рис. 2.45). Вершина параболы находится в точке, А на расстоянии АО = OF/2. Другие точки кривой определяются пересечением прямых, проведенных из произвольных точек 1, 2, … параллельно директрисе, с дугами окружностей, центр которых расположен в фокусе F, а радиус равен расстоянию соответствующих точек до директрисы.

Способ 2 — по заданным вершине, оси и одной из точек параболы (рис. 2.46). Из точек, А и В провести взаимно перпендикулярные прямые до пересечения в точке С. Отрезки АС и ВС разделить на одинаковое число равных частей. Из вершины, А провести лучи в точки деления на отрезке ВС, а из точек деления на отрезке АС — прямые, параллельные оси параболы. В пересечении соответствующих прямых отметить точки одной ветви параболы. Точки другой ветви параболы симметричны относительно оси параболы.

Построение гиперболы. Способ 1 — по заданным вершинам, А и А, и фокусам F, и F гиперболы при AF=A, F,. На оси гиперболы отметить ряд произвольных точек (рис. 2.47): 1, 2…1, 2,… Точки гиперболы определяются построением на пересечении дуг, проведенных из фокусов F и F,. Радиусами дуг служат расстояния от точек до вершин гиперболы, например Я, = АЗ; R₂ = A_t3.

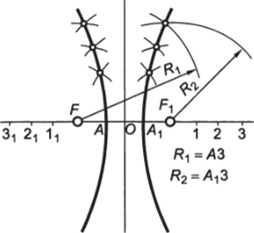
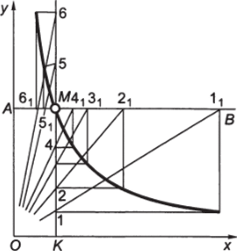
Рис. 2.47. Построение гипербоРис. 2.48. Построение гиперболы лы по ее вершинам и фокусам по ее точке в заданных координатах.

Способ 2 — по заданной точке М в системе координат Оху (рис. 2.48). Через данную точку М провести вспомогательные оси AM и МК, параллельные соответственно Ох и Оу. На оси МК выбрать произвольные точки 1, 2,… через которые провести горизонтальные лучи. Из начала координат О провести через те же точки ряд лучей до пересечения со вспомогательной осью AM в точках 1₁, 2₂,… Опуская из этих точек перпендикуляры на горизонтальные лучи соответствующих номеров, отметить ряд точек, принадлежащих гиперболе.

Построение синусоиды по заданному диаметру начальной окружности (рис. 2.49). Выбрать начало координат для построения синусоиды, совпадающее с точкой А на окружности заданного радиуса R, и на продолжении оси ОА отложить отрезок АА, = 2nR (равный длине окружности). Разделить окружность и отрезок АА, на одина;

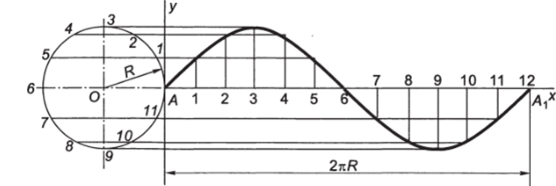
Рис. 2.49. Построение синусоиды 60.

ковое число равных частей и пронумеровать точки деления. Через точки деления окружности провести ряд прямых, параллельных АА,; из точек деления прямой АА, — ряд прямых, перпендикулярных АЛ,. На пересечении этих вспомогательных прямых, имеющих одноименные номера, отметить точки синусоиды.

Вид синусоид имеют многие кривые, изображающие гармонические колебательные процессы или являющиеся проекциями винтовых линий. Для их построения выполнение условия АА, = 2пR не является обязательным, но принцип деления исходной окружности и прямой АА, должен быть сохранен.