Метод вариации произвольных постоянных в теории возмущений

Пусть Я (р, q, I) = #о (Р> Ч. 0 + еЯ,(р, q, t) — функция Гамильтона и е — малый параметр. Кроме того, при е = 0 уравнения Гамильтона р = q = V_p#₀ интегрируемы методом Гамильтона—Якоби, т. е. известен полный интеграл S (q, а, /) уравнения Гамильтона-Якоби.

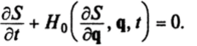
Возьмем полный интеграл 5(q, а, /) в качестве производящей функции канонического преобразования от переменных (р, q) к переменным (а, Р), определяемого формулами.

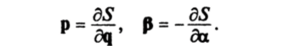
Новый гамильтониан возмущенной системы при е * 0 равен.

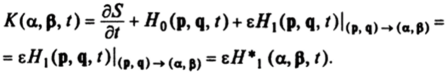
Уравнения (18.1) называются уравнениями возмущенного движения и их правые части имеют порядок е, т. е. переменные а, р эволюционируют медленно. Уравнения (18.1), как правило, неинтегрируемы, но они имеют удобную форму для численного интегрирования.

УРАВНЕНИЯ ВОЗМУЩЕННОГО ДВИЖЕНИЯ В ПЕРЕМЕННЫХ ДЕЙСТВИЕ-УГОЛ И МЕТОД УСРЕДНЕНИЯ. ЭВОЛЮЦИЯ ПЕРЕМЕННОЙ ДЕЙСТВИЕ В ЗАДАЧЕ ВАН ДЕР ПОЛЯ.

Рассмотрим голономную механическую систему с п степенями свободы, описываемую гамильтонианом Н (р, q) = #₀(р, q) + е#,(р, q) и обобщенными силами Q (p, q) = (efi, …, еС?"). Здесь е — малый параметр. Предположим, что известна каноническая замена переменных (р, q) -* (I, ф), где I, ф — переменные действие—угол в задаче с гамильтонианом Я₀(р, q). Тогда.

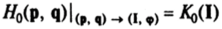
и угловые переменные (ф, …, ф") е 7″" = {ф: ф, е Л¹, mod 2я, /= 1,…, п}. Уравнения движения в исходных переменных получаются из вариационного принципа Гамильтона—Остроградского в форме Пуанкаре.

и имеют вид.

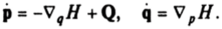
Вариации 5р, 5q произвольны и обращаются в нуль при /= /₀ и t= /]. Вариационный принцип в новых канонических переменных I, ф представляется в форме.

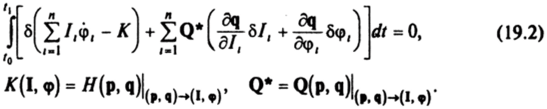
Вариации 61, 6ф также произвольны и обращаются в нуль при /= /₀ и /= /,. Из принципа (19.2) согласно основной лемме вариационного исчисления получим уравнения движения.

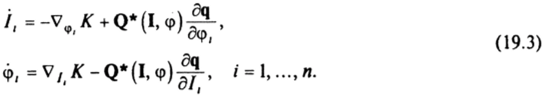
Поскольку новый гамильтониан.

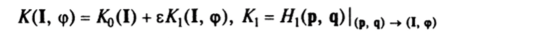
и обобщенные силы содержат малый параметр е, то уравнения.

(19.3) представим в стандартной форме.

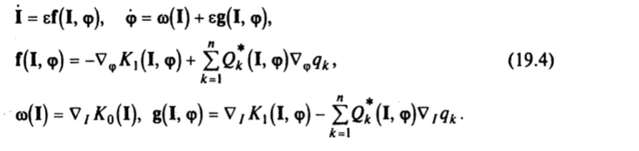
При е = 0 имеем невозмущенную задачу I =0, ф =в>(1), решение которой 1 = 1(0), ф = со (1(0)/-мр (0)). В невозмущенном движении точка движется по тору с постоянной скоростью.

В возмущенном движении при малом е * 0 переменные действие изменяются со скоростью порядка е, а частоты to (I) получают малые добавки порядка б.

Рассмотрим систему с одной степенью свободы (п = 1) и усредненное уравнение.

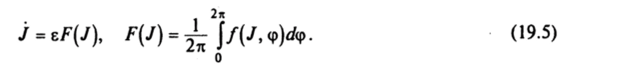
Допустим, что решения уравнений (19.4) и (19.5) с начальными условиями (/(0), ф (0)) и У (0) = /(0) таковы, что функции /(/) и J (t) при I е [0, е'¹] принадлежат компакту К с: Л¹. Кроме того, предполагаем, что функции /(/, ф), ш (/) и F (J) непрерывны вместе со своими первыми производными, когда I, JeKnye S', а функция со (У) 2 со₀>0. В этом случае справедлива теорема.

Т. Решение уравнений (19.4) 1=1(1, 1(0), ф (0)) отличается от решения усредненного уравнения (19.5) J (l) = J (t, 1(0)) на отрезке времени [0, е'¹] на величину порядка е, если е достаточно мало, т. е. справедлива оценка 1(1) — J (t) < се, где с — постоянная, не зависящая от е.

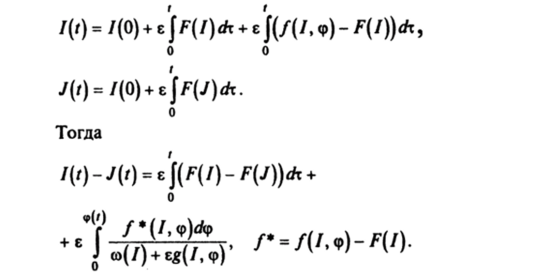
Обозначим I (t) — J (t) = г и, учитывая условие Липшица |F (/) — - /У)| < LI-J, следующее из ограниченности первых производных на К, получим.

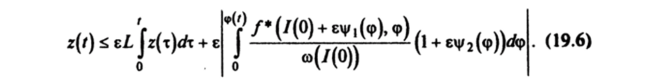
Заметим, что при выводе неравенства (19.6) использовались условия.

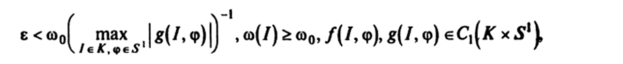
из которых следует обратимость функции q> =.

₂(<�р). Учитывая, что.

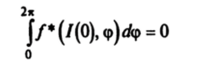
и равенство /*(/(0) + ер,(р), <�р)=/*(/(0), <�р) + еч/₃(<�р), где функция Уз (р) ограничена, получим на отрезке времени [0, е'¹] неравенство.

Здесь М — постоянная, ограничивающая второй интеграл в неравенстве (19.6). Согласно неравенству Гроноулла из (19.7) следует неравенство z (f) ? ef exр (еЦ) и при /е [0, е" ¹] получим z (/) i s zM exp L.

Докажем неравенство Гроноулла. Пусть y (t) = еМ exp (еLt) и удовлетворяет уравнению.

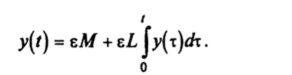
Тогда для х = 2-у справедливо неравенство.

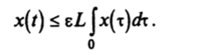
Пусть функция а (/) < 0 такова, что.

Интегральное уравнение (19.8) имеет решение.

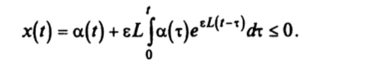
Следовательно, z (t) <, y (t) = zM exp (zLt). T.

Для механической системы с числом быстрых угловых переменных, большим или равном двум, принцип усреднения также юзволяет получить более простую систему уравнений.

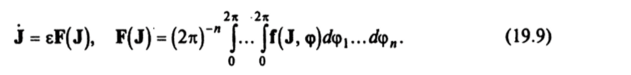
Однако утверждение об е-близости решений усредненной системы (19.9) и исходной системы (19.4) на асимптотически большом интервале времени [0, е'¹], вообще говоря, неверно.

В основе дальнейшего рассмотрения этой проблемы лежит теорема о среднем значении функции f (I, q>) на торе Т^п и на невозмущенной траектории 1 = 1(0), <�р = <�о (1)/ + ф (0) при отсутствии резонансов между частотами о)|(I),…, со«(I). В случае резонансов, когда со (I) • к = 0, к е Z», Z — множество целых чисел, необходимо изменять структуру уравнений (19.9). На практике часто пользуются уравнениями (19.9) для изучения эволюции движения, особенно в тех случаях, когда аттракторы (притягивающие множества) исходной возмущенной системы и усредненной системы совпадают, что дает уверенность в правильности приближенного описания движения системы.

В качестве примера рассмотрим задачу Ван дер Поля — задачу о движении гармонического осциллятора под воздействием неконсервативной силы Q= ер (а² — q²), где (j>, q) е R² — канонические переменные, е — малый параметр, а — постоянная. Функция Гамильтона гармонического осциллятора имеет вид (см. § 6.17).

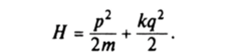
Здесь т — масса материальной точки, к — жесткость пружины. Переходя к переменным действие—угол (/, <�р) по формулам (17.3) и (17.4), получим новый гамильтониан К=®1, а уравнения возмущенного движения (19.3) примут вид.

Усредняя правые части уравнений (19.10) по углу <�р, получим.

Переменная действие J имеет два стационарных значения У, = 0 и /₂ = 2ка²ш' первое из которых неустойчиво, а второе устойчиво. Почти все решения J (l) стремятся к /₂ ^ПР^И f -" «>• В исходных переменных р, q решению У = /₂, <�р = Ы + ф (0) соответствует устойчивый предельный цикл, описывающий автоколебательный процесс.