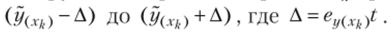Оценивание существенности результатов корреляционного и регрессионного анализа

Оценивание существенности парных корреляции и регрессии

Для практического использования моделей регрессии большое значение имеет их адекватность, т. е. соответствие фактическим статистическим данным. Рассмотрим подходы к проверке адекватности модели на примере линейной регрессии. Традиционно принята следующая схема такой проверки:

• • проверка статистической значимости коэффициентов уравнения регрессии;
• • проверка общего качества уравнения регрессии;
• • проверка выполнимости предпосылок МНК.

Корреляционный и регрессионный анализ проводится обычно для ограниченной (выборочной) совокупности. Поэтому параметры уравнения регрессии, коэффициенты корреляции и детерминации могут быть немного искажены воздействием случайных факторов. Проверка адекватности построенных моделей заключается в выяснении, в какой мере полученные показатели характерны для всей генеральной совокупности и не являются ли они результатом стечения случайных обстоятельств. Общее суждение о качестве модели можно получить, оценив среднюю ошибку аппроксимации по формуле.

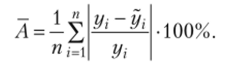
Если средняя ошибка аппроксимации не превышает 9—11%, то можно сделать предварительный вывод, что модель достаточно адекватно описывает наблюдаемую зависимость.

Значимость коэффициента детерминации и соответственно адекватность модели можно проверить с помощью Е-критерия Р. Фишера: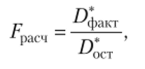

где Д]_)акт — факторная дисперсия (дисперсия, объясненная уравнением регрессии), деленная на число степеней свободы (для парной линейной модели оно равно единице); Д*_ст — остаточная дисперсия (дисперсия, не объясненная уравнением регрессии), деленная на число степеней свободы (для парной линейной модели оно равно (п — 2)).

Для линейной модели связь считается существенной, если Е_расч больше табличного значения Е-критерия (Е_табл) для заданного уровня значимости, а (обычно 0,05) и числа степеней свободы = 1, у₂ = п — 2. На практике при оценивании адекватности уравнения регрессии фактически существующей зависимости возможны следующие ситуации.

• 1. Модель по Е-критерию адекватна, и все коэффициенты регрессии статистически значимы. Такая модель может быть использована для принятия решений и осуществления прогнозов.
• 2. Модель по Е-критерию адекватна, но часть коэффициентов статистически не значима. Модель пригодна для принятия некоторых решений, но не для прогнозирования.
• 3. Модель по Е-критерию адекватна, но все коэффициенты регрессии статистически не значимы. Модель в целом считается неадекватной, на ее основе не принимаются решения и не осуществляются прогнозы.

Проверить значимость уравнения регрессии — значит установить, соответствует ли математическая модель, выражающая зависимость между переменными, экспериментальным данным, а также достаточно ли включенных в уравнение действующих факторов для описания вариации результирующего фактора.

Оценка степени тесноты связи между признаками с помощью коэффициента корреляции, а также параметров уравнения обычно проводится на основе выборки. Возникает вопрос, насколько правомерен вывод о силе корреляционной связи и параметрах уравнения этой зависимости для генеральной совокупности, из которой была произведена выборка, и не являются ли полученные оценки их значений результатом действия случайных причин. В этом случае необходимо оценить существенность линейного коэффициента корреляции и параметров уравнения, и по результатам этого распространить выводы о выборке на всю генеральную совокупность. Для этого может использоваться ?-критерий Стьюдента. Суть проверки заключается в следующем.

Средние ошибки оценки параметров а и Ь линейной модели, а также коэффициента корреляции г вычисляются, но следующим формулам:

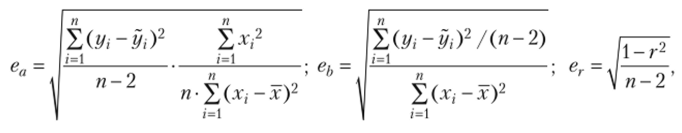
где п — объем выборки.

Расчетные (наблюдаемые) критерии Стьюдента соответственно определяется по следующим формулам:

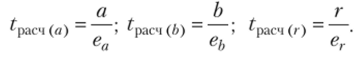
Величину ?_расч сравнивают с табличным значением критерия Стьюдента (?_табл) при числе степеней свободы, равным (п — 2). Параметры а, Ь и коэффициент корреляции (г) можно считать значимыми, если соответствующие ?_расч больше ?_таб_л. Доверительные интервалы будут равны.

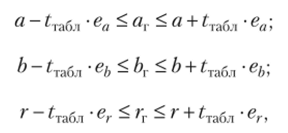
где индекс «г» означает «для генеральной совокупности».

Необходимо отметить, что границы доверительного интервала для коэффициента регрессии не должны содержать противоречивых результатов. Например, запись -1,3 < Ь < 0,5 указывает, что значение коэффициента регрессии одновременно содержит и положительные, и отрицательные величины, и ноль, чего не может быть. В этом случае коэффициент признается незначимым.

Прогноз значения г/, полученный в результате подстановки в уравнение регрессии ожидаемого значения фактора, называют точечным прогнозом. Вероятность абсолютно точной его реализации очень мала. Поэтому рассчитывается значение средней ошибки прогноза и доверительный интервал прогноза с достаточно большой вероятностью. Среднюю ошибку положения линии регрессии в генеральной совокупности при х-х_к определяют следующим образом:

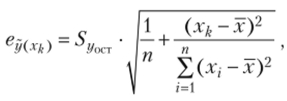
где 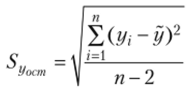 — оценка среднего квадратического отклонения результативного признака от линии регрессии в генеральной совокупности с учетом степеней свободы вариации; п — количество элементов в выборке; х_к — ожидаемое значение фактора х.

Для вычисления доверительных границ прогноза линии регрессии находится значение ?-критерия по таблице Стьюдента на основе числа степеней свободы и принятого уровня значимости. Затем вычисляется предельная ошибка по формуле.

Доверительный интервал прогноза представляет собой диапазон от (У (_Хк) «^д«р) ДО (?(**)+ Л»_Р). Средняя ошибка прогноза для индивидуального значения по правилу дисперсии суммы независимых переменных образуется из ошибки прогноза положения линии регрессии и среднего квадратичного отклонения индивидуальных значений от линии регрессии (остаточной вариации):

Аналогично, доверительный интервал прогноза индивидуальных значений результирующего признака при х = х_к представляет собой диапазон от