Повторные независимые испытания

На практике часто приходится сталкиваться с задачами, которые можно представить в виде многократно повторяющихся испытаний при данном комплексе условий, в которых представляет интерес вероятность числа т наступлений некоторого события А в п испытаниях. Например, необходимо определить вероятность определенного числа попаданий в мишень при нескольких выстрелах, вероятность некоторого числа бракованных изделий в данной партии и т. д.

Если вероятность наступления события А в каждом испытании не меняется в зависимости от исходов других, то такие испытания называются независимыми относительно события А. Если независимые повторные испытания проводятся при одном и том же комплексе условий, то вероятность наступления события, А в каждом испытании одна и та же. Описанная последовательность независимых испытаний получила название схемы Бернулли.

Формула Бернулли

Теорема. Если вероятность р наступления события, А в каждом испытании постоянна, то вероятность Р_{т и} того, что событие, А наступит т раз в п независимых испытаниях, равна

где у—р.

? Пусть Л, и Л, — соответственно появление^[1] и непоявление события Л в г-м испытании (г = 1, 2,…, /?), а В_т — событие, состоящее в том, что в п независимых испытаниях событие Л появилось т раз.

Представим событие В_т через элементарные события Л,.

Например, при п = 3, т = 2 событие.

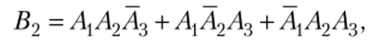
т.е. событие Л произойдет два раза в трех испытаниях, если оно произойдет в 1-м и 2-м испытаниях (и не произойдет в 3-м), или в 1-м и 3-м (и не произойдет во 2-м), или произойдет во 2-м и 3-м (и не произойдет в 1-м).

В общем виде.

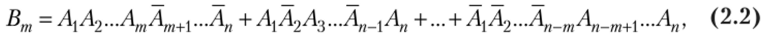
т.е. каждый вариант появления события В_т (каждый член суммы (2.2)) состоит из т появлений события А и п — т непоявлений, т. е. из т событий А и из п — т событий А с различными индексами.

Число всех комбинаций (слагаемых суммы (2.2)) равно числу способов выбора из п испытаний т, в которых событие А произошло, т. е. числу сочетаний С™. Вероятность каждой такой комбинации (каждого варианта появления события В_т) по теореме умножения для независимых событий равна , так как В связи с тем что.

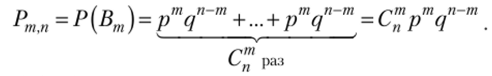
комбинации между собой несовместны, по теореме сложения вероятностей получим.

О Пример 2.1. Вероятность изготовления на автоматическом станке стандартной детали равна 0,8. Найти вероятности возможного числа появления бракованных деталей среди 5 отобранных.

Решение. Вероятность изготовления бракованной детали р = 1 — 0,8 = 0,2. Искомые вероятности находим по формуле Бернулли (2.1):

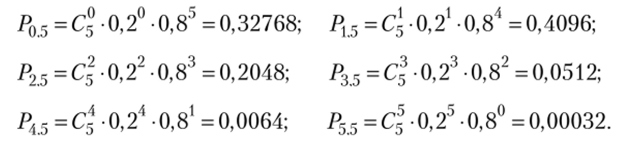
Полученные вероятности изобразим графически точками с координатами (т, Р_тп). Соединяя эти точки, получим многоугольник, или полигон, распределения вероятностей (рис. 2.1). ?

Рис. 2.1.

Рассматривая многоугольник распределения вероятностей (рис.

2.1), мы видим, что есть такие значения т (в данном случае, одно — ти₀= 1), обладающие наибольшей вероятностью Р_тп.

Число т₀ наступления события А в п независимых испытаниях называется наивероятнейшим, если вероятность осуществления этого события Р по крайней мере не меньше вероятностей других событий Р_тп при любом т.

Для нахождения т₀ запишем систему неравенств:

Решим первое неравенство системы (2.3). Используя формулы Бернулли и числа сочетаний, запишем:

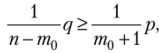
Так как 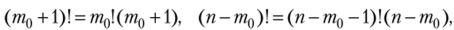то получим после упрощений неравенство откуда (т₀ + 1) д >

>(пщ) р.

Теперь т₀ (р + д) > пр — q или т₀>пр - (7 (ибо р + ц = 1).

Решая второе неравенство системы (2.3), получим аналогично: т₀ <

< пр+ р. Объединяя полученные решения двух неравенств, придем к двойному неравенству:

Отметим, что так как разность пр + р — (пр — д) = р + <7 = 1, то всегда существует целое число т₀, удовлетворяющее неравенству (2.4). При этом если пр + р — целое число, то наивероятнейших чисел два: т₀ = пр + р и т’ъ=пр-ц.

О Пример 2.2. По данным примера 2.1 найти наивероятнейшее число появления бракованных деталей из 5 отобранных и вероятность этого числа.

Решение. По формуле (2.4) 5 • 0,2 — 0,8 < т₀ < 5 • 0,2 + 0,2 или 0,2 ?т₀<

< 1,2. Единственное целое число, удовлетворяющее полученному неравенству, т₀- 1, а его вероятность Л,-, = 0,4096 была получена в примере 2.1. ?

|> Пример 2.3. Сколько раз необходимо подбросить игральную кость, чтобы наивероятнейшее выпадение тройки было равно 10?

Решение. В данном случае р = 1/6. Согласно неравенству (2.4).

или п-5<60<�п + 1, откуда 59 < п < 65, т. е. необходимо подбросить кость от 59 до 65 раз (включительно). ?

• [1] В литературе появление события Л в схеме Бернулли называют также «успехом», а непоявление — «неудачей».