Метод моментов для точечной оценки параметров распределения

Можно доказать, что начальные и центральные эмпирические моменты являются состоятельными оценками соответственно начальных и центральных теоретических моментов того же порядка. На этом основан метод моментов, предложенный К. Пирсоном. Достоинство метода — сравнительная его простота. Метод моментов точечной оценки неизвестных параметров заданного распределения состоит в приравнивании теоретических моментов рассматриваемого распределения соответствующим эмпирическим моментам того же порядка.

А. Оценка одного параметра. Пусть задан вид плотности распределения /(.г, 0), определяемой одним неизвестным параметром 0. Требуется найти точечную оценку параметра 0.

Для оценки одного параметра достаточно иметь одно уравнение относительно этого параметра. Следуя методу моментов, приравняем, например, начальный теоретический момент первого порядка начальному эмпирическому моменту первого порядка: v,= М_{. Учитывая, что v,= М (Х) (см. гл. 8, § 10), М₁ = х_в (см. гл. 17, § 2), получим

Математическое ожидание М (Х), как видно из соотношения.

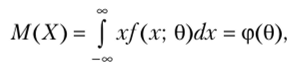
есть функция от 0, поэтому (*) можно рассматривать как уравнение с одним неизвестным 0. Решив это уравнение относительно параметра 0, тем самым найдем его точечную оценку 0*, которая является функцией от выборочной средней, следовательно, и от вариант выборки: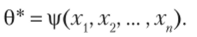

Пример 1. Найти методом моментов по выборке х, х₂,…, х_п точечную оценку неизвестного параметра X показательного распределения, плотность распределения которого /(.г) = Хе~^кх (х > 0).

Решение. Приравняем начальный теоретический момент первого порядка начальному эмпирическому моменту первого порядка: v₍ = М_{. Учитывая, что V, = ЩХ), М, = х_в, получим.

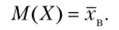
Приняв во внимание, что математическое ожидание показательного распределения равно 1 /X (см. гл. 13, § 3), имеем.

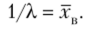
Отсюда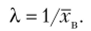

Итак, искомая точечная оценка параметра X показательного распределения равна величине, обратной выборочной средней:

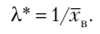
Б. Оценка двух параметров. Пусть задан вид плотности распределения f (x; 0_Г 0₂), определяемой неизвестными параметрами 0, и 0₂. Для отыскания двух параметров необходимы два уравнения относительно этих параметров. Следуя методу моментов, приравняем, например, начальный теоретический момент первого порядка начальному эмпирическому моменту первого порядка и центральный теоретический момент второго порядка центральному эмпирическому моменту второго порядка:

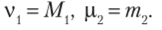
Учитывая, что v, = М (Х), р, = D (X) (см. гл. 8, § 10), М_{ = х_в, т₂ = = D_n (см. гл. 17, § 2), получим.

Математическое ожидание и дисперсия есть функции от 0, и 0₂, поэтому (**) можно рассматривать как систему двух уравнений с двумя неизвестными 0! и 0₂. Решив эту систему относительно неизвестных параметров, тем самым получим их точечные оценки 0* и 02- Эти оценки являются функциями от вариант выборки:

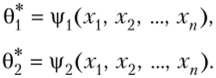
Пример 2. Найти методом моментов по выборке х_{, х_у …, х_п точечные оценки неизвестных параметров, а и о нормального распределения.

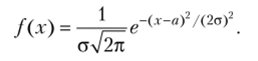
Решение. Приравняем начальные теоретические и эмпирические моменты первого порядка, а также центральные и эмпирические моменты второго порядка:

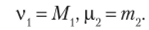
Учитывая, что v, = М (Х), р₂ = D (X), М, = х_в, т.₂ = D_i:, получим.

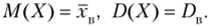
Приняв во внимание, что математическое ожидание нормального распределения равно параметру а, дисперсия равна а² (см. гл. 12, § 2), имеем:

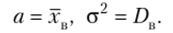
Итак, искомые точечные оценки параметров нормального распределения:

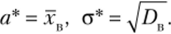
Замечание 1. Для оценок неизвестных параметров можно приравнивать не только сами моменты, но и функции от моментов. В частности, этим путем получают состоятельные оценки характеристик распределений, которые являются функциями теоретических моментов. Например, асимметрия теоретического распределения (см. гл. 12, § 9).

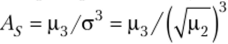
есть функция от центральных моментов второго и третьего порядков. Заменив эти теоретические моменты соответствующими эмпирическими моментами, получим точечную оценку асимметрии.

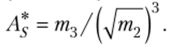
Замечание 2. Учитывая, что у[т^ = yjl = а_в, последнюю формулу можно записать в виде.

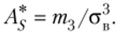
Далее эта оценка будет принята в качестве определения асимметрии эмпирического распределения (см. гл. 17, § 9).