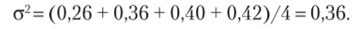Сравнение нескольких дисперсий нормальных генеральных совокупностей по выборкам одинакового объема. 
Критерий Кочрена

Пусть генеральные совокупности Х_х, Х₂…^распределены нормально. Из этих совокупностей извлечено / независимых выборок одинакового объема иипо ним найдены исправленные выборочные дисперсии .v,², s^, …, sf, все с одинаковым числом степеней свободы k = п — 1.

Требуется по исправленным дисперсиям при заданном уровне значимости, а проверить нулевую гипотезу, состоящую в том, что генеральные дисперсии рассматриваемых совокупностей равны между собой:

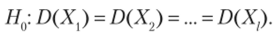
Другими словами, требуется проверить, значимо или незначимо различаются исправленные выборочные дисперсии.

В рассматриваемом случае выборок одинакового объема можно по критерию Фишера — Снедекора (см. § 8) сравнить наибольшую и наименьшую дисперсии; если окажется, что различие между ними незначимо, то подавно незначимо и различие между остальными дисперсиями. Недостаток этого метода состоит в том, что информация, которую содержат остальные дисперсии, кроме наименьшей и наибольшей, не учитывается.

Можно также применить критерий Бартлетта. Однако, как указано в § 20, известно лишь приближенное распределение этого критерия, поэтому предпочтительнее использовать критерий Кочрена, распределение которого найдено точно.

Итак, в качестве критерия проверки нулевой гипотезы примем критерий Кочрена — отношение максимальной исправленной дисперсии к сумме всех исправленных дисперсий:

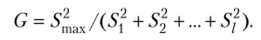
Распределение этой случайной величины зависит только от числа степеней свободы k — п -1 и количества выборок /.

Критическую область строят правостороннюю, исходя из требования, чтобы вероятность попадания критерия в эту область в предположении справедливости нулевой гипотезы была равна принятому уровню значимости:

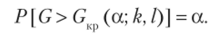
Критическую точку С_к|)(а; к, /) находят по таблице приложения 8, и тогда правосторонняя критическая область определяется неравенством G > G_k, а область принятия нулевой гипотезы — неравенством G < С_кр.

Обозначим значение критерия, вычисленное по данным наблюдений, через G_m6ji и сформулируем правило проверки нулевой гипотезы.

Правило. Для того чтобы при заданном уровне значимости, а проверить гипотезу об однородности дисперсий нормально распределенных совокупностей, надо вычислить наблюдаемое значение критерия и, но таблице найти критическую точку.

Если G_mfn < С_кр — нет оснований отвергнуть нулевую гипотезу.

Если G_{m (yi} > G_k)i — нулевую гипотезу отвергают.

§ 22. …о значимости выборочного коэффициента корреляции 327.

Замечание. Если требуется оценить генеральную дисперсию, то при условии однородности дисперсий целесообразно принять в качестве ее оценки среднюю арифметическую исправленных выборочных дисперсий.

Пример. По четырем независимым выборкам одинакового объема п = 17, извлеченным из нормальных генеральных совокупностей, найдены исправленные дисперсии: 0,26; 0,36; 0,40; 0,42. Требуется: а) при уровне значимости 0,05 проверить нулевую гипотезу об однородности генеральных дисперсий (критическая область — правосторонняя); б) оценить генеральную дисперсию.

Р е ш е н и е. а) Найдем наблюдаемое значение критерия Кочрена — отношение максимальной исправленной дисперсии к сумме всех дисперсий:

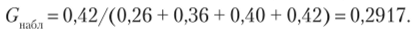
Найдем, но таблице приложения 8, по уровню значимости 0,05, числу степеней свободы k = 17 — 1= 16 и числу выборок /= 4 критическую точку G_Kp(0,05; 16; 4) = 0,4366.

Так как G_[ia&i < G — нет оснований отвергнуть нулевую гипотезу об однородности дисперсий. Другими словами, исправленные выборочные дисперсии различаются незначимо.

б) Поскольку нулевая гипотеза справедлива, в качестве оценки генеральной дисперсии примем среднюю арифметическую исправленных дисперсий: