Работа и энергия

Обратимся к уравнениям движения. Как мы видели,.

Умножим это равенство слева и справа скалярно на вектор скорости:

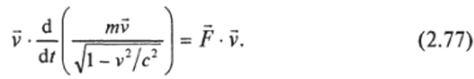
Можно показать, что левая часть равенства (2.77) равна так что равенство (2.77) принимает вид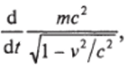

Это уже знакомое нам равенство (2.75). Учитывая, что ус1/ = <3г, вместо (2.78) можно написать.

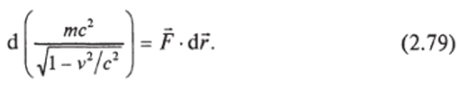
Здесь 6 г — малое перемещение частицы, а в левой части равенства стоит малое изменение величины, стоящей в скобках. Обозначая эту величину буквой ?, равенство (2.79) запишем в виде.

Величина.

называется энергией частицы, величина.

называется работой силы на малом перемещении 6г (малость предполагает, что силу можно считать постоянной в пределах перемещения).

Равенство (2.80) означает, что изменение энергии частицы на малом перемещении равно работе на этом перемещении.

Суммируя малые изменения энергии, мы получим полное изменение энергии на определенном куске траектории, а разбив этот кусок на малые перемещения и просуммировав элементарные работы, получим полную работу. Формально, интегрируя равенство (2.80), будем иметь.

Здесь Е_г ?, — конечное и начальное значения энергии, интеграл в правой части вычисляется вдоль траектории.

Работа может быть как положительная, так и отрицательная, и энергия частицы соответственно будет возрастать или убывать. Если скорость частицы равна нулю, формула (2.81) дает.

Эта величина называется энергией покоя частицы. Величина.

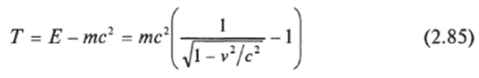
называется кинетической энергией частицы.

При х .

При малых скоростях из формулы (2.85) с учетом (2.86) получим.

Это определение кинетической энергии в ньютоновской механике.

Если масса частицы не изменяется (а в принципе она может изменяться), равенство (2.83) примет вид.

Изменение кинетической энергии частицы равно работе действующей на нее силы.

При малых скоростях это дает равенство.

Равенство (2.89) позволяет найти изменение скорости частицы на определенном участке траектории под действием силы.

Понятие работа исчерпывается определением (2.82). Понятие энергия частицы исчерпывается формулой (2.81). Однако само понятие энергия пронизывает всю физику и его смысл не исчерпывается формулой (2.81). В общем случае под энергией понимается способность к совершению работы. Когда говорят, что некоторая система обладает энергией, под этим понимают то, что эта система способна совершить некоторую работу, и эта работа будет равна убыли энергии системы. Летящая пуля обладает кинетической энергией, и это означает, что она способна совершить работу и действительно совершает ее, застревая в мишени и производя соответствующие разрушения. Заряженный аккумулятор обладает энергией и может совершить работу, но чтобы извлечь эту энергию, нужно иметь электромотор. В связи с этим возникает вопрос о смысле формулы (2.84). Что такое энергия покоя частицы?

Формула (2.84) дает связь между массой и энергией. Если энергия системы увеличивается на величину Д?, ее масса возрастает на величину Ат = ДД/с². Заряженный аккумулятор имеет большую массу, чем незаряженный, хотя на бытовом уровне это и не проявляется.

Задача 2.13. Заряженный аккумулятор обладает энергией 2 10⁵ Дж. На сколько уменьшится его масса при полной разрядке?

Решение. Указанной энергии соответствует масса Дт = ДЕ/с² = = 2 -107(3 -Ю⁸)² = 2,2 10~¹² кг. Это слишком малая величина для того, чтобы как-то проявиться (но, с другой стороны, это масса 10¹⁵ атомов водорода).

Можно ли, однако, считать, что вся величина тс² есть энергия в смысле способности совершения работы, или есть какой-то остаток, из которого уже ничего извлечь нельзя? Оказывается, можно. В принципе из любого тела массой т можно извлечь энергию тс² и превратить ее в работу (хотя, при существующем положении дел, это будет себе дороже).

Задача 2.14. В задаче 2.10 рассматривались кинематические аспекты ускорения космического корабля. Какую работу нужно совершить, чтобы разогнать корабль массой 1000 т до скорости 0,9с?

Решение. Согласно формуле (2.88) работа равна конечной кинетической энергии корабля. По формуле (2.85) находим 7 = 1,3тс². Переводить эту величину в джоули нет смысла, а оценить ее можно следующим образом. Солнце за 1 с теряет на излучение 4 млн т. На Землю падает порядка 30 кг солнечной энергии. Энергия, вырабатываемая всеми устройствами на Земле, на два порядка меньше. Таким образом, для разгона корабля нужна энергия порядка той, что вырабатывается на Земле за год.

Формулу (2.82), определяющую работу, можно представить, в другом виде. Малое перемещение 6г = тсЬ, где т — единичный касательный вектор к траектории в точке нахождения частицы, а дз — длина дуги, соответствующая перемещению. Имеем:

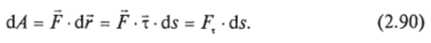
Здесь =/'•! — тангенциальная составляющая силы (заметьте, эта величина отрицательна, если угол между векторами силы и перемещения тупой).

Видим, что изменение кинетической энергии частицы обусловлено только тангенциальной силой.

Работа, совершаемая за единицу времени, называется мощностью. Обозначая мощность буквой /V, будем иметь.

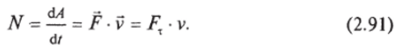
Возвращаясь к формуле (2.78), видим, что скорость изменения кинетической энергии частицы равна мощности действующей силы.

Замечание. Говоря о силе, действующей на частицу, мы имели в виду полную (результирующую) силу. Если частица взаимодействует с несколькими телами, результирующая сила представится векторной суммой всех действующих сил, и работа этой силы представится суммой работ всех сил. Если автомобиль движется с постоянной скоростью, его кинетическая энергия не изменяется, и работа действующих на автомобиль сил равна нулю. Куда же девается энергия, получаемая при сгорании топлива в двигателе автомобиля? Она идет на работу силы тяги, а эта работа идет на работу против силы сопротивления, возникающей при взаимодействии автомобиля с воздухом и дорогой. Работа силы сопротивления в конечном итоге переходит в кинетическую энергию молекул воздуха. Таким образом, сжигая топливо в двигателе, мы просто обогреваем атмосферу (но автомобиль при этом движется). При ускорении автомобиля энергия топлива идет еще и на увеличение кинетической энергии, но эта энергия безвозвратно теряется при торможении. Самая экономичная езда — это езда с постоянной скоростью (при этом обогрев атмосферы минимален).

Резюмируя все сказанное, отметим, что работа — это механизм, посредством которого другие виды энергии переводятся в кинетическую энергию частицы и кинетическая энергия частицы переводится в другие виды энергии.