Простейшие математические операции с комплексными числами

Для вычислений с комплексными числами имеются разнообразные средства — инженерные калькуляторы, математические программы для компьютеров (в том числе свободно распространяемые в Интернете, например Wise Calculator), которые существенно упрощают расчеты. В ряде случаев приходится рассчитывать вручную. Поэтому полезно вспомнить некоторые математические положения.

Как известно, любое комплексное число А может быть записано в трех формах — показательной, алгебраической и тригонометрической. Показательной формой записи А = Ae^ja мы уже пользовались. Для перехода к равнозначной записи А в алгебраической форме А = а_л + ja₂ рассмотрим рис. 2.4.5, из которого очевидно, что комплексное число А может быть выражено суммой двух комплексных чисел — действительного а_{ (проекция вектора А на ось действительных чисел) и мнимого ja₂ (проекция вектора А на ось мнимых чисел). Из рис. 2.4.5 очевидна и равнозначность тригонометрической формы записи А = Л (со$а + у sin а).

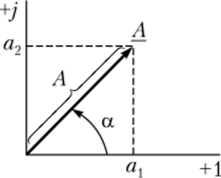
Рис. 2.4.5. Иллюстрация к трем формам записи комплексного числа

Выбор той или иной формы в каждом конкретном случае диктуется удобством осуществления нужной математической операции с комплексными числами: при суммировании удобна алгебраическая форма, при умножении и делении — показательная. Впрочем, это замечание имеет значение, если для вычислений используется обычный калькулятор. При использовании математических программ, например МаСЬсаб, или калькуляторов с комплексными числами можно использовать любую форму комплексного числа.

Напомним некоторые определения и правила действия с комплексными числами, известные из математики и часто используемые при анализе цепей синусоидального тока.

11ереход от одной формы записи к другой очевиден из рис. 2.4.5: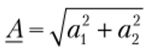

заменить на 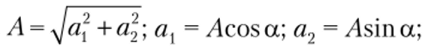а — см. в табл. 2.4.2.

Комплексное число А называют действительным, если а₂ = 0, при этом аргумент комплексного числа равен нулю или тг, а вектор А располагается на комплексной плоскости вдоль (при а_{ > 0, а = 0) или противоположно (при а_л < 0, а = ±7г) положительному направлению оси действительных чисел. Комплексное число называют мнимым, если а_л = 0; аргумент мнимого числа может принимать значения ±л/2 в зависимости от знака а₂. На комплексной плоскости мнимое число изображают вектором, совпадающим.

Таблица 2.4.2

Значения аргумента комплексной величины

Значения ах и а2	а2 < 0.	а2 = 0.	а2 > 0.

с положительным направлением оси мнимых чисел (а = п/2) или противоположно ему (а = -п/2).

Запишем в трех формах выражения для единичных действительных и мнимых комплексных чисел (случай А = 1):

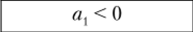
Суммирование комплексных чисел удобно осуществлять в алгебраической форме записи. Если А = а_х + ]а₂, В = 6, + ]Ь₂ и С =_Л + В, то С = с_{ + ]с₂, где с, = а_{ + 6, и с₂ = а₂ + Ь₂.

При умножении комплексных чисел их модули перемножают, а аргументы суммируют, следовательно, умножение удобно проводить в показательной форме записи. Если А = Ае^)а, В = Веи С = А В, то С = Се^7У, где С = АВ и у = а + р.

При делении комплексных чисел их модули делят, а аргументы вычитают, т. е. если С = А/В, то С = Се>'^{_} где С = А/В и у = а — р.

Комплексные числа А и А* называют сопряженными, если их модули равны, а аргументы отличаются только по знаку: А = Ае^)а и А* = Ае~^{, а}.

Опираясь на перечисленные правила, нетрудно доказать справедливость следующих соотношений:

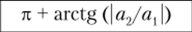
Пример 2.4.1. Представления синусоидальных величин комплексными.

На рис. 2.4.6 представлена осциллограмма тока и напряжения пассивного двухполюсника. Запишите выражения для мгновенных значений напряжения и тока, приняв за начало отсчета точку 0. Найдите напряжение и ток для момента времени = Т/12. Запишите комплексные амплитуды напряжения и тока. Постройте векторную диаграмму на комплексной плоскости.

Решение

Угловая частота со = 2п/Т= 314 рад/с,/= 50 Гц. В момент времени? = 0 напряжение проходит нулевую фазу, т. е. начальная фаза напряжения равна нулю:

= 0. Начало синусоиды тока сдвинуто вправо от начала отсчета времени, значение начальной фазы тока, отсчитываемое от начала синусоиды до оси, отрицательно: у, = —7г/4. Мгновенные значения напряжения и тока.

При = Г/12 фаза напряжения, а = со/, = 2я/Г (Г/12) = тг/6 и напряжение и = 200нт (л/6) = 100 В, фаза тока р = (Ь_х — я/4) = л/6 — я/4 = -л/12 и ток / = = 6мп (-я/12) = -1,55 А.

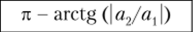
Рис. 2.4.6. Осциллограммы тока и напряжения пассивного двухполюсника

(к примеру 2.4.1)

Комплексные амплитуды напряжения и тока в показательной форме 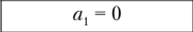Комплексные амплитуды напряжения и тока в алгебраической форме.

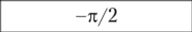
Векторная диаграмма представлена на рис. 2.4.7.

Рис. 2.4.7. Векторная диаграмма токов и напряжений к примеру 2.4.1

Длины векторов пропорциональны в выбранном масштабе модулям комплексных амплитуд. Начальная фаза напряжения р" = 0, поэтому вектор напряжения направлен по оси +1, начальная фаза тока (|/_# = -к/А) отложена от оси +1 по направлению вращения часовой стрелки.

Пример 2.4.2

Выполните задания рассмотренного примера 2.4.1, приняв за начало отсчета времени точки 0, и 0, (см. рис. 2.4.6, а).

Решение

Векторные диаграммы представлены на рис. 2.4.8, а, б.

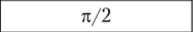
Рис. 2.4.8. Векторные диаграммы токов и напряжений (к примеру 2.4.2)

Пример 2.4.3. Представления комплексных величин синусоидальными

Напряжение и ток пассивного двухполюсника равны Ц = (20 + /Ю) В, / = = (5 + >3) А. Найдите мгновенные значения напряжения и тока.

Решение

Модули комплексных действующих значений напряжения и тока:

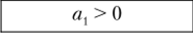
Их начальные фазы.

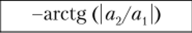
Комплексные действующие значения напряжения и тока в показательной форме.

Комплексные амплитуды напряжения и тока.

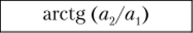
Мгновенные значения напряжения и тока.

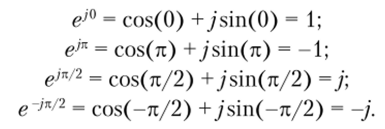
Упражнение 2.4.2*.

В табл. 2.4.3 заданы комплексные действующие значения напряжений и токов цепи. Найдите мгновенные напряжения и токи (начальные фазы в радианах, частота 100 Гц).

К упражнению 2.4.2

Таблица 2.43