Уравнения подобия конвективного теплообмена

В соответствии со второй теоремой подобия критерии, определяемые из системы дифференциальных уравнений, описывающих конвективный теплообмен, одновременно являются и критериями, получаемыми из уравнения, представляющего решение этой системы, поэтому, используя полученные выше критерии подобия, уравнение подобия конвективного теплообмена можно записать в следующей общей форме:

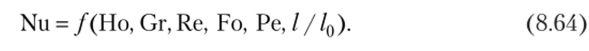
Число гомохрониости, Но и число Фурье Ро являются определяющими критериями для нестационарных процессов. При стационарных процессах, для которых Э? /Эт = 0 и с1т_х / с! т = 0, как это следует из (8.6а) и (8.18), эти критерии отсутствуют. Отметим, что наибольший практический интерес представляет определение коэффициента теплоотдачи, а при установившемся режиме. Это позволяет в дальнейшем ограничиться составлением уравнений подобия только для стационарного теплообмена. В этом случае (8.64) записывают так:

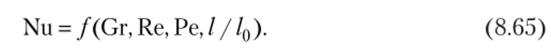
Учитывая, что Ре = ЯеРг, уравнение подобия (8.65) можно записать в следующем виде:

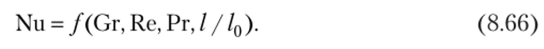
В приведенных уравнениях симплекс / / /₀ — отношение линейных размеров твердого тела (например, отношение диаметра трубы к ее длине) — характеризует условия геометрического подобия.

В отдельных случаях (8.66) упрощается. Так, в случае вынужденного турбулентного потока можно не учитывать влияние естественной конвекции, т. е. пренебречь числом Грасгофа:

При свободном движении, т. е. когда вынужденная конвекция отсутствует, в (8.66) не будет входить число Рейнольдса:

Условия подобия процессов конвективного теплообмена получены в предположении, что физические характеристики теплоносителя (теплопроводность, вязкость, теплоемкость и др.) постоянны во всей области протекания процессов. В действительности эти физические свойства зависят от температуры, причем для разных теплоносителей характер зависимостей X = /(?), V = /(?), с_р = /(?) различен. В процессе теплообмена температура теплоносителя изменяется, следовательно, в общем случае меняются и его физические свойства. Подобие процессов выполняется тем полнее, чем меньше относительное изменение этих свойств. При значительном изменении физических свойств строгое подобие различных процессов в общем случае становится невозможным. В этих условиях можно говорить лишь о приближенном подобии. Это обстоятельство должно учитываться при обобщении опытных данных.

В тех случаях, когда изучение конвективного теплообмена на натурном образце затруднительно, последний заменяют его моделью. Метод замещения образца моделью называется моделированием. Согласно третьей теореме подобия подобие модели и образца соблюдается при подобии условий однозначности и равенстве определяющих чисел подобия. При соблюдении этих условий выводы, полученные на модели, могут быть распространены на образец. Моделирование на основе теории подобия является одним из основных методов научного изучения конвективного теплообмена.