Кривые распределений. 
Правовая статистика

Графическое изображение интервальных рядов распределения облегчает их анализ и позволяет выявлять закономерности распределения вариант. Этого можно достичь, если увеличивать объем исследуемой совокупности, что соответственно приведет к уменьшению величины интервала и увеличению их числа. При графическом изображении этих данных мы получим некоторую плавную кривую линию, которая для гистограммы относительных частот будет являться некоторым пределом. Эту линию называют кривой распределения, т. е. гистограмма позволяет получить приближенное представление о кривой распределения. Эта кривая характеризует в обобщенном виде вариацию признака и закономерности распределения частот внутри совокупности. Иными словами, кривая распределения есть графическое изображение в виде непрерывной линии изменения частот в интервальном вариационном ряду, которое функционально связано с изменением вариант. Известно много форм кривых распределений, но наиболее известной и чаще всего применяемой в практике статистических исследований является кривая нормального распределения. Нормальное распределение зависит от двух параметров: средней арифметической х и среднего квадратического отклонения а. Его кривая выражается уравнением.

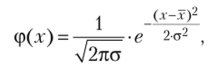
где ф (т) — ордината кривой нормального распределения; ей п — математические постоянные; х — средняя величина; а — среднее квадратическое отклонение.

Вид кривой нормального распределения приведен на рис. 5.12.

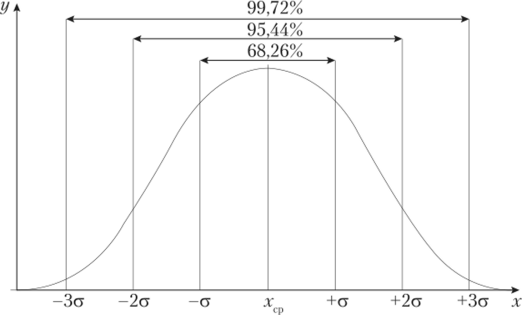
Рис. 5.12. График кривой нормального распределения с указанием соотношения площади под кривой нормального распределения в зависимости от расстояния от средней арифметической.

Для многих явлений и процессов, изучаемых правовой статистикой, характерен нормальный закон распределения, кривая которого на графике зависимости у от х (см. рис. 5.12) отличается рядом особенностей, которые применительно к статистической совокупности можно сформулировать следующим образом:

• 1) куполообразная форма, симметричная относительно значения х = = х_ср = Mo = Me, где х_ср — значение средней арифметической среди имеющихся вариантов изучаемого признака, Мо — мода, Me — медиана;
• 2) асимптотическое приближение к оси абсцисс в обе стороны от х_ср. Чем больше конкретный вариант отличается от х_ср, тем меньше его частота. При этом в интервале х_ср ± а (а — среднее квадратическое отклонение) находится приблизительно 68,3% всех единиц изучаемой совокупности, в интервале х_ср ± 2а — 95,4% единиц, в интервале х_ср± За — 99,7%.

Если нужно получить теоретические частоты / при выравнивании интервального вариационного ряда по кривой нормального распределения, то можно воспользоваться приближенной формулой.

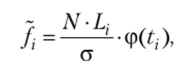
где N = Yjfi — сумма всех частот интервального вариационного ряда; Lj — величина г-го интервала; а — среднее квадратическое отклонение;

х^/ — X

t_i = ——нормированное отклонение серединных значений интервалов а.

от средней арифметической показателя; х — серединные значения интервалов вариационного ряда; х — средняя величина показателя. Значения ф (?,) для нормированных отклонений t_x находят по статистической таблице плотности нормального распределения. При этом следует иметь в виду, что функция ф (?) — четная, т. е. ф (-?) = ф (?)> поэтому в таблице приводят значения функции только для положительных значений аргумента.

Замечание. Значения функции ф (?) можно находить также, используя приложение MS Excel. Для этого на «панели инструментов» нажимаем кнопку f_v далее в «категории» выбрать «статистические» и в них функцию НОРМРАСП из списка функций. Появляется окно ввода значений. Вводим в строку окна ввода «X» значение аргумента функции ф (?) — t, в строку окна ввода «Среднее» — 0, в строку окна ввода «Стандартное откл.» — 1, в строку окна ввода «Интегральная» — 0. Получаем нужное табличное значение функции ф (?).

При помощи этой формулы мы получаем теоретическое распределение, заменяя им наблюдаемое распределение. Объективная характеристика соответствия теоретического и наблюдаемого распределений может быть получена при помощи специальных статистических показателей, которые называют критериями согласия. Для оценки близости наблюдаемых и теоретических частот применяются критерии согласия Пирсона, Романовского, Колмогорова и др. Наиболее распространенным является критерий согласия К. Пирсона у}, который можно представить как сумму отношений квадратов расхождений между /-и /к теоретическим частотам:

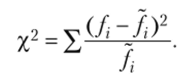
Вычисленное значение критерия х²_раСч необходимо сравнить с табличным (критическим) значением Х²_таб.т Табличное значение определяется по статистической таблице распределения Пирсона. Оно зависит от принятой доверительной вероятности р и числа степеней свободы k (при этом k = т — 3, где т — число интервалов в вариационном ряду распределения). Если Х²расч ^{< <} Х²табл> ^то расхождения между наблюдаемыми и теоретическими частотами распределения могут быть случайными и предположение о близости наблюдаемого распределения к нормальному не может быть отвергнуто.

Пример. Статистическая совокупность данных о длительности нахождения дела в производстве суда представлена в виде следующего интервального вариационного ряда (табл. 5.2).

Таблица 5.2

Данные о длительности нахождения дела в производстве суда.

При помощи критерия согласия Пирсона необходимо проверить предположение о близости наблюдаемого распределения длительности нахождения дела в производстве суда к нормальному распределению.

Решение. Прежде всего найдем среднюю арифметическую!⁷ и среднее квадратическое отклонение а. Для того чтобы определить среднее значение на основе интервального вариационного ряда, необходимо сначала найти серединные значения интервалов:

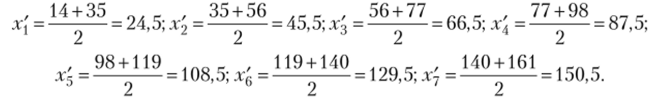
Теперь находим среднее значение по формуле средней арифметической взвешенной 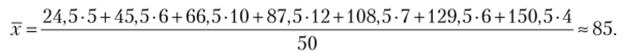Далее, но формуле для взвешенной дисперсии находим.

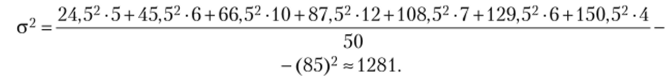
Тогда среднее квадратическое отклонение равно: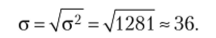

Таким образом, нам нужно проверить предположение о близости наблюдаемого распределения к нормальному распределению со средней арифметической, равной 85, и средним квадратическим отклонением, а = 36.

Вычислим теоретические частоты f_v воспользовавшись приведенной выше формулой. Получим:

Находим значение критерия Пирсона:

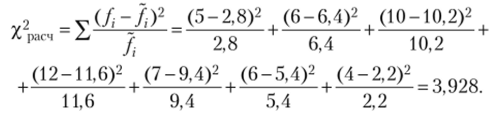
Табличное значение х²_табл определяется, но статистической таблице распределения Пирсона. Оно зависит от принятой доверительной вероятности р и числа степеней свободы k = т — 3, где т — число групп в ряду распределения. Выбираем доверительную вероятность р = 0,95. Так как таблица распределения Пирсона составлена для уровня значимости, а = 1 -р, то при выбранной доверительной вероятности р = 0,95, а = 1 — 0,95 = 0,05. Число групп в ряду распределения т = 7, следовательно, число степеней свободы k = т — 3 = 7- 3 = 4. Из таблицы распределения Пирсона Х²_табл = 9,488. Так как %²_расч < Х²табл"^то расхождения между наблюдаемыми и теоретическими частотами распределения могут быть случайными и предположение о близости наблюдаемого распределения длительности нахождения дела в производстве суда к нормальному распределению не может быть отвергнуто.

Замечание. Необходимые табличные значения можно находить, используя приложение MS Excel. Для этого на «панели инструментов» нажимаем кнопку /_г, далее в «категории» выбираем «статистические» и в них — функцию ХИ20БР из списка функций. Появляется окно ввода значений. В строку окна ввода «Вероятность» вводим уровень значимости, а = 1 — р, где р — доверительная вероятность, а в строку окна ввода «Степени свободы» — число степеней свободы k = m- 3, где т — число групп в ряду распределения, ОК. Получаем нужное табличное значение %²_табл.

На компьютерной графике основаны некоторые процедуры классификации (группировки) данных, анализа динамики: выявления тенденции, сравнения динамики разных социально-правовых показателей и т. д.

Все виды графических изображений могут характеризовать правовые явления в абсолютных данных и относительных показателях.

В заключение обратим внимание на некоторые общие правила чтения графиков. Его необходимо начинать с чтения заголовка графика. Осмыслив его, мы поймем, о чем говорит график, какие сведения мы можем и какие нельзя из него получить. Затем надо разобраться в специфических условностях данного графика (шкалы, масштабы, единицы измерения, условные базы и т. д.).

Выяснив строение графика и разобравшись в элементах его графического образа, надо представить себе, что будут обозначать те или иные изменения образа.

Общее восприятие графического образа как целого полезно начинать, игнорируя шкалы и масштабы. По мере приобретения навыков в дальнейшем чтение производится с определением числового значения отдельных точек, линий, их наклонов и других элементов графика.