Покрытия и разбиения множеств, принцип включения-исключения

Систему множеств {X_v …, X_k} называют покрытием множества X, если X = Х_х и … u X_k. Разбиением множества X называют его покрытие {X_v …, X_k), если Xj nXj=0 для различных i, j е {1,…, k}.

Подмножества Х_х, …, X_k множества X называются блоками покрытия (разбиения), число k блоков — порядком покрытия (разбиения). Последовательность записи блоков несущественна в силу коммутативности операции объединения. Тривиальным блоком разбиения называют одноэлементный блок. Разбиение {Y_u …, Y_m) множества X называется продолжением разбиения {Х_х, …, X_f,} того же множества, если для любого i = 1, …, т найдется номер j е {1,…, &} такой, что У) с Ху Отсюда следует, что т > k.

В комбинаторике встречаются схемы выборок, в которых «-множество X состоит из элементов k > 1 типов (иначе, X разбивается на k блоков). Число разбиений «-множества на k блоков мощностей щ,…, n_k (обозначается С («, «!,…, n_k)) равно.

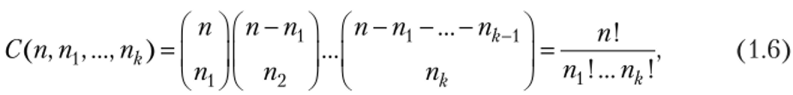
где п = п_х + … + п_к. Числа С (п, щ,…, щ) называются полиномиальными коэффициентами, число С (п, п_{,…, п_к) совпадает с коэффициентом при мономе x"¹…x_k^k в каноническом виде действительного полинома (х_{ + … + x_k)ⁿ. Заметим, что С (п, п_{} п₂) = С"¹.

Числа различных разбиений 77-множеств (разбиений /7-множеств на k непустых блоков) называют числами Белла (числами Стирлинга 2-го рода).

Для разбиения конечного множества X выполнено правило суммы:

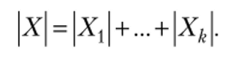
Получим соотношение для покрытия множества X. Пусть U — универсум, X с U, характеристической функцией множества X (обозначается ф_х) называется функция ф_х: U —> {0, 1}, где фх (х) = 1 х е X.

Отметим свойства характеристических функций:

1) для любых подмножеств X, Y универсума выполнены соотношения:

^а) Фхпу⁼ ФхФу; б) ФхиУ⁼ Фх + Фу «ФхФу; ^в) Фх — 1 ^_ Фх>

2) для любого конечного множестваХсправедлива формула X = X Фх (-^Г);

леХ Из свойств 16, 2 следует обобщенное правило суммы для покрытия — I Х| < < |Xj I + … + X_k;

3) если {Х_и Х_к} — разбиение множества X; ф, — — характеристическая функция множества X_i9 i е {1, k}, то Фх = Ф1 + ••• + Ф* в соответствии со свойством 1;

4) если {Х|,Х_к} — покрытие множества X, го из законов де Моргана следует:

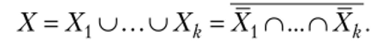
Тогда в соответствии со свойством 1 получаем.

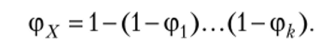
Для точного подсчета или оценки порядка множества X через порядки множеств покрывающей системы используется метод включения-исключения (теоремы 1.1—1.3).

Теорема 1.1. Мощность объединения конечного числа множеств равна.

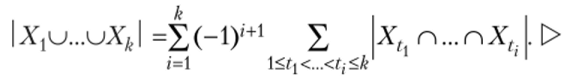
Имеется более общая формула включения-исключения. Пусть каждый из п элементов обладает или не обладает свойствами z_v …, z_k. Обозначим через n (t_v …, tj) число элементов, обладающих свойствами z_t ,…, Z,. (и, возможно, некоторыми другими), где {t_v …, t_t) с {1, …, k}, и через п₀ — число элементов, не обладающих ни одним из свойств z_{,…, z_k.

Теорема 1.2. Пусть s- =? w (^,…,^), i = 1, …, k, тогда.

1 <�ц <…

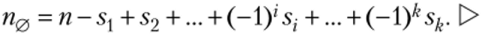
Теорема 1.3. Для числа п_г элементов, обладающих ровно г свойствами, верно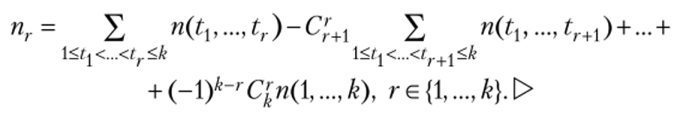

Пример 1.6 (задача о беспорядках) Перестановка (t_u …, t_k) множества {1, …, к}, в которой * i для всех i = 1, …, называется беспорядком. Используя формулу включения-исключения, посчитаем число д (/г) беспорядков среди всех k перестановок степени к. Определим i-с свойство перестановок как «tj = /», i е {1,…, к). Тогда в формуле включения-исключения (теорема 1.2) следует положить: = q (k) и n (t_u …, tj) = (к — /)! — количество пере становок, в которых t_r = г для r= 1,i. Следовательно,.

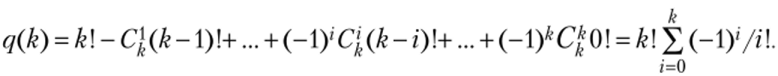
oo.

Учитывая разложение числа#^-1 в числовой ряд, =? (-1)^,/Л, получаем отсюда.

/=0.

при больших значениях к асимптотическую оценку: q (k) ~ kle~^l. t>