Понятие о классификации двоичных функций

При анализе полное перечисление всех б.ф. и их свойств не под силу современным электронно-вычислительным машинам (ЭВМ) уже при числе переменных п > 5. В связи с этим используется разбиение функций на классы, где внутри классов функции обладают близкими свойствами. Если число классов невелико, то анализ облегчается, ведь по свойствам представителей классов можно судить о свойствах остальных функций. Подход к исследованию множеств, заключающийся в разбиении их на классы, называют классификацией. Булевы функции можно классифицировать по различным характеристикам: весам, степеням нелинейности и т. д. Важным с точки зрения приложений в криптологии является подход, основанный на применении групп преобразований.

Пусть G — некоторая группа преобразований множества V_n, порядок группы G удовлетворяет неравенствам: 1 < G < (2″)!. Булевы функции f (pc^…, х_п) и |/(xj,…, х_п) называют эквивалентными относительно группы G, или G-эквивалентными, если в G найдется подстановка g, при которой |/(х) = f (g (x)). Обозначим это отношение f =^Gi или/= |/, если в контексте группа G определена однозначно. Данное бинарное отношение на множестве Р₂(п) при любой группе G является отношением эквивалентности, так как выполнены свойства:

• а) рефлексивность —/=^с/(в этом случае g = е);
• б) симметричность — f =^G |/, тогда |/ =^Gf
• в) транзитивность — / =^G |/, |/ =^G z_y тогда f =^G z.

Итак, множество Р₂(п) разбивается на классы в связи с эквивалеицией =^с. Обозначим класс эквивалентности, содержащий функцию /, через [_;f]_G, заметим, что 1 < IL/lcl — IС|. Ес ЛИ IIЛс I = 1, го / неизменна при всех преобразованиях g е G, т. е. функция / инвариантна относительно группы G, или G-инвариантна. Степень инвариантности / относительно преобразований группы G отражает понятие группы инерции. Группа инерции функции / в группе G есть множество преобразований из G (обозначаемое J_G(J)), не меняющих /:

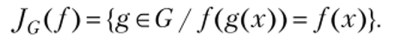
МиожествоУ^^ — подгруппа группы G. Если jc (f) 1=1, то говорят, что функция / имеет тривиальную группу инерции в группе G.

Теорема 6.11. Для всякой функции/е Р₂ справедливо: {/]q = G / /L/c (/)l•.

А Класс f_G есть множество функций (|/(х): |/(х) = f{g{x)), ge G}. Пусть g е G. Определим, сколько преобразований g' из G дают ту же функцию, что и g, т. е. f (g (x)) =f (g'(x)).

Сделаем замену переменной у = g{x). Тогда х = g~^l{y) и из последнего равенства имеем.

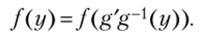
Данное равенство выполнено «g» = g’g~^{ е Jc,(D- Следовательно, g' имеет вид: g'=g" g, и всего таких преобразований jc (f)> где данное число не зависит от выбора g. ?

Заметим, что теорема 6.11 — частный случай леммы Бернсайда (теоремы 4.23).

Укажем основные пять групп подстановок V_n, используемых для классификации б.ф.

1. Группа S_n перестановок переменных состоит из п подстановок вида.

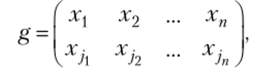
где (jpj₂, — перестановка чисел (1,2,…, п).

Функция f{x) называется симметрической, если она инвариантна относительно группы S_n, т. е. J_s {f) = S_n. Симметрической б.ф. является, например, сумма всех конъюнкций ранга k от п переменных, 0 < k < п.

2. Группа Z_w инвертирований переменных (группа сдвигов) состоит из подстановок.

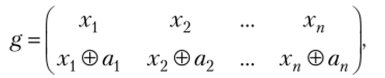
где (a_t, а_ъ а_п) е V", 11"| = 2″ .

3. Группа Джевонса Q_n {группа однотипности, геометрической эквивалентности) есть произведение групп S_n и Х_п. Группа Q" состоит из подстановок вида.

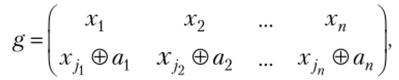
где (j_lf …J_n) — перестановка (1,…, п), (a_v …, а") е V_n.

Подстановка g переставляет переменные и инвертирует некоторые из них, iQj =п2″.

4. Группа GL_tl(2) линейных подстановок {полная линейная группа). Подстановки задаются обратимой двоичной матрицей А порядка п: g (x) = хА,

GL"(2) = П (2″ -2');

/=0.

5. Группа AGL_n{2) аффинных подстановок {полная аффинная группа) — произведение групп GL_n и Она состоит из подстановок g{x) = хА ® /;,.

где А = (ciy) — обратимая двоичная матрица порядка вектор b = (b_v …,.

Ь")е AGL_n{2) = 2"п'(2″ ^-2');

1=0.

Каждая из групп S_n, Q", GL_n{2) является подгруппой группы AGL_n{2).

Отметим аналитические свойства эквивалентных функций. Утверждение 6.3. Пусть / =^с|/, тогда:

• 1) II/NMI;
• 2) если G < AGL_n(2), то deg/ = deg|/;
• 3) если G е {S_IV Ъ_п> Q,_?}, то числа существенных переменных/ и |/ равны.

Л Свойство 1 следует из неизменности веса функции при любой подстановке g.

При любой аффинной подстановке g степень нелинейности функции f (g (x)) не возрастает, поэтому второе свойство следует из цепи соотношений.

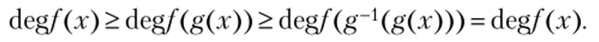
Третье свойство следует из того, что любая подстановка g из G преобразует пару соседних векторов множества V_n в пару также соседних векторов. ?

Изложим идею классификации б.ф. с использованием групп преобразований V_n. Важной проблемой классификации является задача конструктивного перечисления, т. е. получение списка представителей всех классов эквивалентности.

• 1. Сначала выбирается какой-либо способ перечисления всех функций из р₂(^)> ^т-^е— генерируется последовательность {/ц./ъ/з, •••}• Способы построения этой последовательности могут быть различными, например, перебор всех функций, начиная с функции малого веса или с функции малой степени нелинейности и т. д. Возможно, сразу не удается обеспечить, чтобы все эти функции лежали в разных классах эквивалентности, поэтому выполняем п. 2.
• 2. Полагаем /П) = f_{ и подсчитываем [/с (/⁽¹))|. Далее берем /₂ и проверяем, выполнено ли отношение /₂ = ^GfG). Если выполнено, то переходим к /₃. Если не выполнено, то полагаем /<²> = /₂ и подсчитываем 1/г;(У⁽²)) I и т. д.

Взяв очередную функцию f_i из исходной последовательности, проверяем, эквивалентна ли она одной из отобранных ранее функций /О, Если эквивалентна, то переходим к f_M. Если не эквивалентна, то полагаем f (m+1) ₌ f. _и вычисляем jc (f (^m+^) (способы вычисления jc (f)I для б.ф./ рассмотрены ниже), после чего проверяем равенство.

Если (6.17) выполнено, то классификация закончена.

Алгоритм классификации упрощается, если известно число т классов эквивалентности: не требуется вычислять порядки групп инерции и проверять равенство (6.17). В этом случае классификация завершена, если построена последовательность /(В,/(2), 0.

Таблица 63

Число классов эквивалентности б.ф. относительно групп.

Определенное неудобство такой классификации заключается в том, что мощности классов эквивалентности могут заметно различаться (см. теорему 6.11).

В табл. 6.3 даны результаты подсчета числа классов эквивалентности для пяти указанных групп при п < 6. Из таблицы видно, что для классификации б.ф. от п > 6 переменных этот подход оказывается неэффективным. Вместе с тем подход к классификации функций, основанный на G-эквивалентности, представляет интерес для оценки числа неэквивалентных ключей некоторых криптографических схем.

С целью укрупнения классов эквивалентных функций рассматриваются и другие отношения эквивалентности. Булевы функции f (x_x, …, х_п) и |/(х_1?…, х_п) называют (G, Н)-эквивалентными, где Gи Я-группы подстановок множеств V" и V_x соответственно, если найдутся подстановки ge G и h е Я, при которых |/(х) = h (f (g (x))), обозначается /=(СЯ) |/.

В случае булевых функций |я| делит 2. Если группа Я тривиальна, то (G, Я)-эквивалентность и G-эквивалентность совпадают, если IЯ | = 2, то содержащий f (x_x,…, х_п) класс (С, Я)-эквивалентности состоит из всех б.ф., G-эквивалентных либо /, либо / © 1.

Для вычисления групп инерции часто используется класс эвристических методов. Они выполняются в два этапа. Сначала выбирается набор каких-либо достаточно просто вычисляемых параметров (называемых «эвристиками»), по значениям которых можно либо сделать вывод «функции не эквивалентны» или «группа инерции тривиальна» и др., либо уменьшить число вариантов, подлежащих перебору для получения окончательного ответа.

Пример 6.2. Определение | /_{S i}(/)| для б.ф. /.

Представим/(.х_х,…, х₆) в виде суммы однородных многочленов: f (x_x,…, х₆) = 1 ® (r) (Xj ® хг₃ ® х₄) ® (х_{х₂ © Х Ъ © ^Х4^Хб) © ^Х2^Х3^Х4 © ^ГДе fi ~ ОДНОРОДНЫЙ многочлен степени i, i = 1, 2, 3, 4: /, = х_{ © х₃ © х₄; /₂ = х_хх₂ © х^с_ъ © х₄х₅; /₃ = х^х₃х₄; /₄ = х_эXjpcsfiQ. Составим матрицу M (f) частот встречаемости переменных х_х, …, х₆ в однородных многочленах.

Если подстановкаg Е J_s (/), то применение ее к столбцам матрицы M (f) не изменит матрицу, т. е. g может переставить только одинаковые столбцы матрицы. В примере одинаковы лишь столбцы, соответствующие х₃ и х₄. Следовательно, подстановки из /$ (/) оставляют на месте x_v х₂, х₅, х₆ и, быть может, переставляют х₃ и х₄. Применяя к многочлену f (x_{,…, Л'₆) транспозицию (х₃, х₄), получаем, что изменяется /₂(.г" …, r_s), значит, |Д.(/)| = 1.0.

Для определения групп инерции функций в разных группах могут использоваться веса, степени нелинейности подфункций, число существенных переменных, число вхождений в члены фиксированной степени в полиноме и другие инварианты. Группу J_z (/) для б.ф. / можно найти из решения относительно а_{1…, а_п системы уравнений, составленной в виде равенств коэффициентов АНФ функций /(xj,…, х_п) и f (x_x © а_х,…, х"© а_п) при одинаковых мономах.